3.4.1.1 供应商披露成本信息

首先考察披露信息时，供应商的利润，即。

若供应商实际执行了披露成本信息，那么实际成本s 对供应商S 和制造商M 来说都是已知的。对于给定的s，供应商会选择最优批发价w来使得自身的利润最大化：

其一阶条件为：

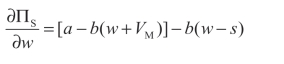
二阶条件为：

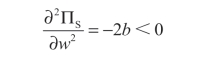
因此，供应商的最优批发价为：

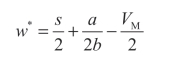
对于制造商来说，制造商会选择签订最优合同，选择最优的单位利润 VM 来使自己的利润最大化：

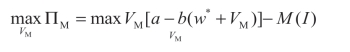
其一阶条件为：

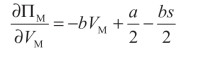
二阶条件为：

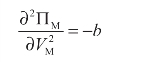
因此，制造商的最优合同单位利润为：

此时得出，当投资额I 固定，供应商披露成本信息时的均衡条件，其中利润随成本 c 的增加而降低，故取。相应地，供应商披露成本时的其他均衡条件如下：

供应商最优化批发价：

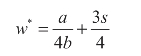
供应商的单位利润：

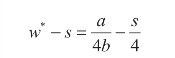
制造商的最优单位利润：

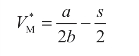
制造商的定价：

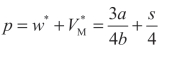
制造商的订货数量：

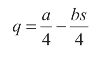
供应商的利润函数（上标D 表示披露）：

制造商的利润函数：

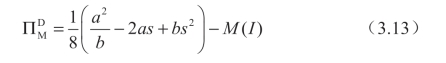(www.daowen.com)

3.4.1.2 供应商隐藏成本信息

本节考察供应商选择隐藏信息时供应商的决策。隐藏信息时，供应商的利润为：

把上式对c 求导得一阶条件：

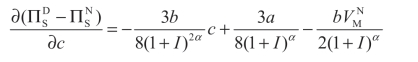
二阶条件：

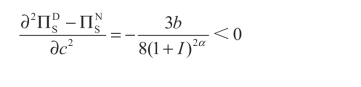
因此，最优的决策为：

而且：

其中：

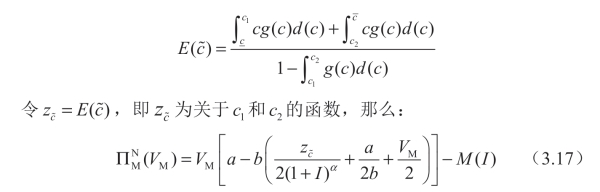
其一阶和二阶条件分别为：

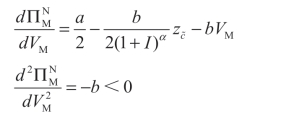
最优决策为：

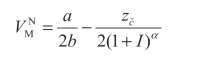
在供应商隐藏信息时，制造商选择的单位利润与成本c 的后验分布的范围有关，与成本在披露和隐藏的临界点有关。c 的期望成本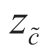越高，供应商的利润越小，从而可以得到隐藏状态下的均衡结果如下：

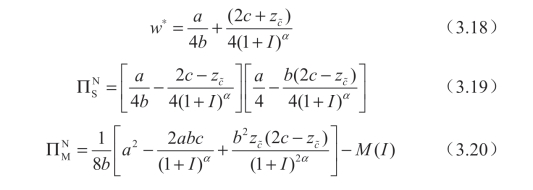
3.4.1.3 分析披露条件

根据前两节得到的供应商披露和隐藏时的利润，计算可得：

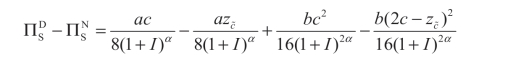
由于 c1 和 c2 为临界点，因此，当　c　 = c1或　c　 = c2时：

3.4.1.4 数值分析

本节中，根据前三节的分析结论，通过使用MATLAB 求解，给定外生变量时，成本的临界值 c1 和 c2 得到披露条件。然后，可以计算得到供应商和制造商的期望利润，并对同等外生变量情况下，与3.2 节中的供应商事先做出承诺且投资外生情况下的供应商和制造商的利润进行比较，分析两种不同信息共享方式下的供应链成员的利润。

首先，可以得到供应商不做事先承诺且投资外生情况下供应商和制造商的期望利润，如下：

表3.10　基于固定定价的合约中两种信息共享方式的利润比较

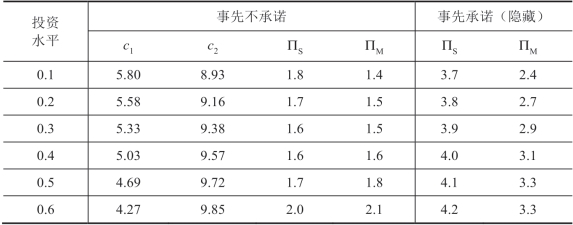
首先，需要说明的是，当供应商事先做出承诺时，我们选择的是隐藏信息时供应商和制造商的利润，由3.2 节的结论可知，无论投资水平如何，供应商选择隐藏信息时的利润总大于披露信息时的利润。

在供应商的披露政策事先不确定时，随着投资水平的增加，如果供应商披露信息的成本范围逐渐扩大，且供应商和制造商的期望利润也在增加，则说明制造商投资水平的增高可以有效促进供应商进行信息披露，并且能够有效增加双方的利润，从而优化供应链的整体效能。但是，我们也可以观察到，在供应商的披露政策事先不确定时，供应商和制造商的利润均要比披露政策提前确定（隐藏）的时候更低一些。