在供应商事先做出承诺且投资外生情况下,供应商与制造商进行博弈的行为顺序,如图3.1 所示。在图中,S 代表供应链上游的供应商,M 代表供应链下游的制造商,双方具体的决策顺序如下:首先,供应商承诺是否向制造商披露产品成本;其次,制造商对供应商进行投资;然后,供应商获得制造商投资后,得到实际的生产成本,并按照承诺对制造商进行成本信息的披露或隐藏;然后,制造商根据获得的成本信息,确定制造商单位产品利润;最后,供应商确定批发价。

图3.1 在供应商事先做出承诺且投资外生情况下,供应商与制造商进行博弈的行为顺序
设定相关的参数符号如下:
w:批发价格;
p:零售价格;
VM:固定利润加成法下供应商的绝对单位利润;
ηM:百分比加成法下供应商的利润百分比;
q:市场需求,市场需求确定时,需求与订货量相等;
c:未投资前供应商获得的单位成本;
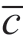 :成本预测范围上限;
:成本预测范围上限;
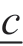 :成本预测范围下限;
:成本预测范围下限;
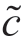 :隐藏信息时制造商根据已知信息做出更新后的成本;
:隐藏信息时制造商根据已知信息做出更新后的成本;
s:制造商投资效应后降低的实际单位成本;
I:制造商实际投资水平;
ΠS:供应商的利润;
ΠM:制造商的利润;
 :供应商隐藏信息情况下,供应商的利润;
:供应商隐藏信息情况下,供应商的利润;
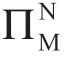 :供应商隐藏信息情况下,制造商的利润;
:供应商隐藏信息情况下,制造商的利润;
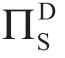 :供应商披露信息情况下,供应商的利润;(https://www.daowen.com)
:供应商披露信息情况下,供应商的利润;(https://www.daowen.com)
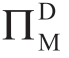 :供应商披露信息情况下,制造商的利润。
:供应商披露信息情况下,制造商的利润。
为简化模型,我们考虑最简单的二级供应链,供应商提供原材料并出售给制造商,制造商加工并出售给终端经销商、顾客等。考虑最常见的线性需求函数如下:
![]()
而制造商的定价措施有两种:

在日常生活中,这是最常见的两种定价方式。其中公式(3.2)是单位产品利润固定的定价方式,为绝对加成定价,VM 是单位利润;公式(3.3)是单位产品提取固定比例的定价方式,为百分比加成定价,单位产品利润百分比是 Mη 。
制造商会采用投资激励措施来降低供应商的生产成本c,例如,对供应商生产线以及供应线的改善,提高生产工艺和生产流程以及新生产技术的引进,等等。这种投资对成本的降低效应用可以用I 来衡量,而制造商的投资成本为M(I )。假定M(I )在I=0 处为零,且为凹函数,即
![]()
那么制造商的利润函数为:

如图3.2 所示。
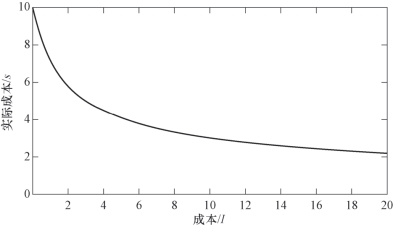
图3.2 成本降低对数线性模型(以c =10,α =0.5 为例)
其中,I 为真实的投资水平。投资水平I 越大,实际单位成本s 越小,且边际成本越低,符合实际经验。对于供应商和制造商来说,成本c 的经验概率为两者的共同知识(Common Knowledge),成本c 服从概率为g ( c )的分布,期望值是μ,方差是σ2,其中σ2>0。
那么供应商的利润函数为:
![]()
考虑到研究的方便性,做两点假设:
(1)为简化计算,供应商若进行披露信息,可忽略披露成本不计;
(2)承诺可信,供应商做出承诺,事后一定会履行,不存在事后违背承诺的现象。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





