我们现在考虑最复杂的合约，即菜单合约[MC]，格式为{w(q)，L(q)}，其中，供应商收取批发价w 和一次性费用L，这两者都取决于q。L＞0 可以解释为特许经营费（Franchise Fee）；L＜0 对应一个上架费用（Slotting Fee）。事件的顺序如下：首先，供应商提供菜单合约；接着，买方根据自己的私人成本信息 c 选择订单数量 q 并支付给供应商w(q)q+L(q)。对于任何透露的q 选择，供应商可以推断出买方的真实成本c，所以根据显示原理（Baron 和 Myerson，1982），{w(q)，L(q)}等价于一个合约菜单也就是说，如果买方宣布他的成本是 c ′，然后他会选择一个合约条款（w(c′)，L(c′)）。

如果具有实际成本 c 的买方声明 c′并因此接受合约条款（w(c′)，L(c′)），由于L(c′)是一次性付款，与p（或q）无关，所以买家将设定：

因此，参与者的利润可以给出：

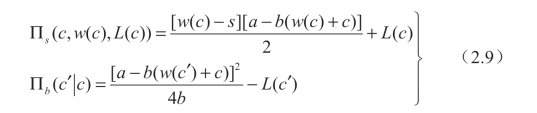
定义Πb(c) ≡ Πb(c|c)，因此，供应商优化菜单合约的问题可以表述为：

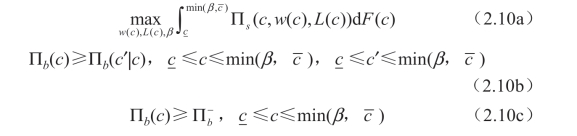
其中，激励相容性约束(2.10b）确保买方只有在他真实地报告其成本时才能使其利润最大化，私有理性约束（2.10c）确保买方的参与。

引理2.2 总结了供应商菜单合约的最优均衡解。引理2.2 的详细证明归入附录A2.3 中。

引理2.2（供应商菜单合约的最优决策）

当F(c)具有减的反失效率函数时，即F(c)/f(c)随c 增加时，供应商的最优决策表示为：

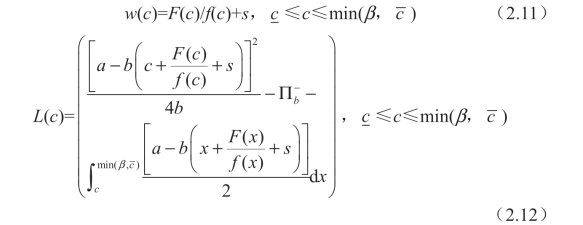
其中，β 满足：

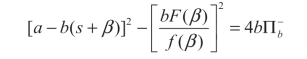
当进一步假设非对称信息 c 服从均匀分布，其均值为μ且方差为σ2时，供应商的最优期望利润如下：

如果σ≤σII：

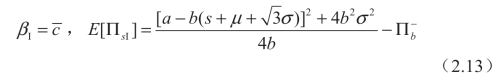
则其他：(www.daowen.com)

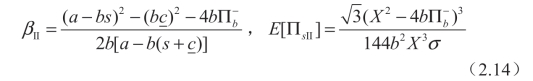
其中：

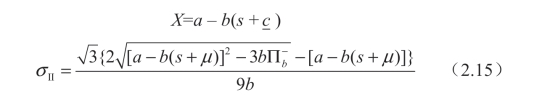
与批发价合约的情况相似，引理 2 .2 表明供应商的期望利润 E [∏s]在所有情况下都降低。虽然当σ ≤σII（因为β =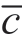 ）时不存在关停点，但当σ ＞σII 时，因有利类型的交易供应商将受益，因为∂βII/∂σ ＜0，关停点随σ 降低，从而导致了β＜ 。

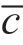当采用的是菜单合约而不是批发价合约时，命题2.2 和表2.4 分别是命题2.1 和表2.2 的对应情况。命题2.2 的证明见附录A2.4。

命题2.2（信息不对称对供应商期望利润的影响）

如果供应商关于不对称信息c 的先验分布服从均匀分布，他的期望利润是先验分布方差的拟凸函数，其最小值点在max(σII，σIII)处，其中，σIII 由下面等式唯一确定。

其中：

附录A2.4 给出了命题2.2 的详细证明。与命题2.1(b)不同，虽然我们未能清晰地表明临界点 max(σII，σIII)是产品盈利能力 a/[b(s+μ)]的递增函数，σII 随着 a/[b(s+μ)]的增加而增加，但我们可以用数值算例来验证命题2.1(b)的结果。当不对称信息c 服从截断伽玛分布时，数值实验见表2.4。

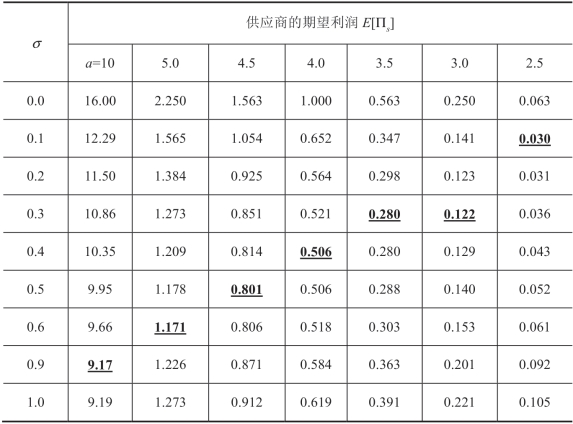
很容易看出，表2.4 中的数值结果与表2.2 中的模式类似，因此，它证实了我们的主要结论：供应商偏好两种极端情况，对称信息或完全不对称信息，而不管其所使用的合约格式如何。另外，表2.4 还表明，关键的临界点随着a 值从左到右递减而下降，这意味着产品的收益率越低（即a/[b(s+μ)])，就越容易观察到临界点。此外，将结果与简单的批发价合约的结果进行比较，我们观察到供应商期望利润增加的条件范围随着σ 的增加而变化，通过采用更复杂的合约格式不会显著改变（即收缩或扩大），即使这种“更复杂”的合约格式确实可以增加供应商的期望收益（与批发价合约相比）。

表2.4　合约菜单下方差对供应商利润的影响

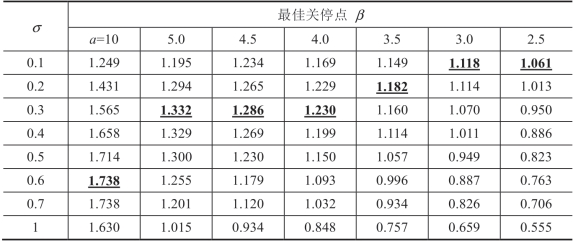
当不对称信息c 服从截断伽玛分布时，表2.5 显示了与表2.3 中相同的效果。数值模式也与表2.3 中的价格合约相同，因此在此略去，将在2.3.3 节中讨论。

表2.5　合约菜单下方差对关停点的影响