我们首先考虑最简单的合约，即批发价合约[w]，其中供应商只能指定一个固定的批发价w。事件的顺序描述如下：首先，供应商收取单位批发价w；其次，买方根据他的私人成本信息c 确定订单数量q，并支付给供应商wq。使用逆向归纳法来求出均衡解。

由于具有成本c 的购买者的利润为Πb=(p-w-c)(a-bp)，所以根据供应商给出的w，购买者的最优响应是q=[a-b(w+c)]/2 或 p=[a+b(w+c)]/(2b)。因此，供应商的问题可以表述为：

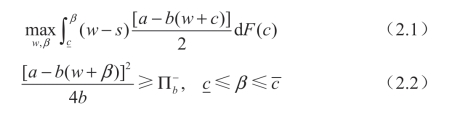
其中，公式（2.1）表示当c≤β 时，供应商的利润为(w-s)[a-b(w+c)]/2，当c＞β 时为0；公式（2.2）是买方的参与约束。除w 之外，关停点β也是供应商的决策变量。随着信息不对称水平（即σ）的增加，如果供应商继续与所有类型的买方进行交易，它将不得不支付大量的信息租金，因此，为了使其期望利润最大化，供应商需要通过平衡交易效率和信息租金来确定最佳的关停点β（即成本低于该关停点β 时，诱导买方签署合约）。这种说法也适用于菜单合约。

引理 2.1 总结了当非对称信息 c 服从均值为μ和方差为σ2 的均匀分布时，供应商关于批发价合约的最优均衡解。引理2.1 的详细证明见附录A2.1。

引理2.1（批发价合约下供应商最优决策）

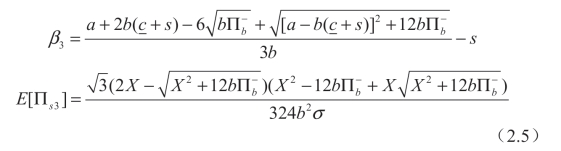
其中：

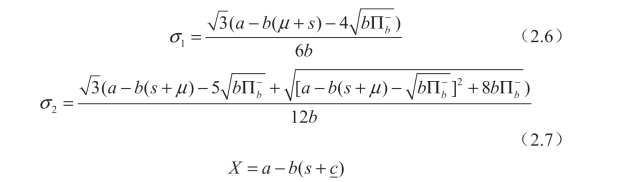
根据引理 2.1，可以很容易地观察到，在所有情况下，批发价格 w和供应商的期望利润E[∏s]随着他对买方边际成本μ（即E[c]）期望值的上升而下降。这是直观的结果，因为期望成本μ 越高意味着成本越高，因此，买方收取更高的零售价格，这将推动市场需求下降，并迫使供应商设定较低的批发价格并产生较低的期望利润。

与期望成本μ 的效果相反，下面结果显示标准差σ 对最优批发价格和供应商期望利润的影响是非常不直观的。引理2.1 表明，没有关停点（即σ ≤σ1），批发价格w 和供应商的期望利润E[∏s]独立于σ，是常数；当σ1＜σ ≤σ2 时，随着 σ 的增大，w 和 E[∏s]减小；否则，w 随着 σ 的增加而增加，然而，在这种情况下 E[∏s]不是单调的。下面的命题清楚地证明，随着 σ 的增加，E[∏s]先减少再增加，并在max(σ2，σ3)点处达到其最小值，因此，供应商的期望利润可以被看作σ 的一个拟凸函数，这表明供应商获得更准确的买方成本信息并不总是受益的。当c 服从均匀分布时，供应商对信息不对称水平的偏好总结在命题2.1 中。命题2.1的详细证明归入附录A2.2。

命题2.1（信息不对称对供应商期望利润的影响）

如果供应商关于非对称信息c 的先验知识服从均匀分布，则：(www.daowen.com)

（a）她的期望利润是先验分布方差的拟凸函数，其最小值点是max(σ2，σ3)，其中：

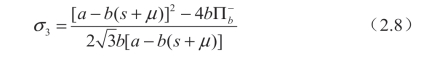
（b）临界点 max(σ2，σ3)随着产品的利润率（即a/[b(s+μ)])的增加而增加。

上述声明是在一个限制性假设下获得的，即c 服从均匀分布。尽管这种假设在研究中很常见，但我们仍然考虑其他分布形式（如正态分布、截断伽玛分布等）来检验我们的结论是否可以推广。以下是其他分布相关结果的介绍。当非对称信息c 服从截断伽玛分布时（由于成本不能为零，我们将γ 截断为非常小的正数），很难如引理2.1 那样从供应商问题中获得闭形式解。本研究使用FORTRAN 程序和IMSL（1994）子程序包以数值算例方式解决此问题和其他后续问题。

假设不对称信息 c 服从截断伽玛分布，表 2.2 给出了不同a 值和σ值组合下的数值结果。表 2.3、表 2.4 和表 2.5 中的数值实验使用了与表 2.2 中相同的参数值。

表2.2　方差对价格合约下供应商利润的影响

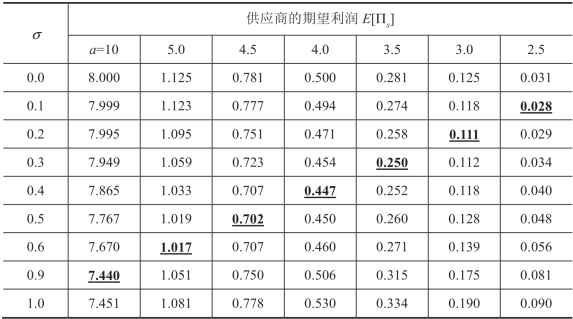
参数值：q=a-p，s=1，μ=1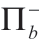， =[a-b(s+μ)]2/(24b)。

表2.2 显示，对于任何给定的a 值，当σ位于粗体和带下划线数字的上方时，供应商的期望利润（即E[Πs]）随着σ增加而降低，而当σ位于粗体和带下划线数字的下方时，供应商的期望利润随着σ增加而降低，因此，这一现象证实了命题2.1 中的说法。从附录2.1 的推导中可以很容易地看出，“σ≤σ1”，供应商的期望利润是恒定的，如果 c 的概率分布具有很长的右尾（如在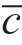 =∞时的伽玛分布中），则均匀分布下的σ 不会出现，因此表2.2 不存在“σ≤σ1”区域，这与在引理2.1 中的均匀分布结果不同。

正如 L au 等（2007）指出的那样，比率 a /[b(s+μ)]是衡量产品盈利能力的指标。较高的 a/[b(s+μ)]比率意味着需求对价格上涨较不敏感，使渠道能够收取更高的零售价格并从市场中获取更大的利润。根据这一定义，表2.2 中的数值实验表明，临界点（即与粗体和下划线数字相对应的σ值）受产品盈利能力的影响（a/[b(s+μ)]），即利润率越高，临界点越大，就像命题2.1(b)所表述的那样。

在本节研究中，所有的数值结果和结论，例如，前一段中的表述和结论，都是通过参数网格化生成的多组测试问题确认后才做出的。列出的数值结果只是我们数据的一小部分。至于σ 对最佳关停点β 的影响，我们可以证明，如果σ≤σ2，则由于β =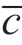 ，关停点随着σ 的增加而增加，即只要信息不对称水平不高，供应商就会与所有买方签订合约；否则，σ ＞σ2，由于∂β3/∂σ＜0，关停点随着σ 的上升而下降，即当信息不对称水平超过某个阈值时，关停点策略将起作用（即β 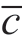＜ ），因此供应商只会与有利的买方类型（即 c≤β3）进行交易。此外，当σ 足够高时，关停点β 随着σ 的增加而减小，这表明更多不利的买家被淘汰出市场。为了更清楚地揭示这种非单调模式，表2.3 给出了不对称信息c 服从截断伽玛分布时，在a 值和σ 值的各种组合下的最佳关停点β 的数值结果。

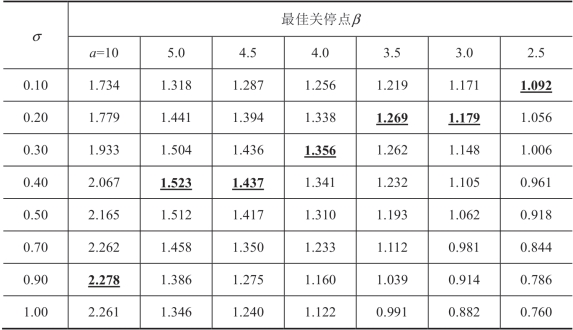
表2.3 中的数值结果清楚地证实了上述结论：当超过一定水平时，必须考虑关停点策略。此外，随着市场规模 a（或产品的盈利能力a/[b(s+μ)]）的下降，该门槛值降低。注意，这个结果对于解释供应商期望利润的拟凸性非常有用，将在2.3.3 节中讨论。

表2.3　价格合约下方差对关停点的影响