1.3.4.1 问题描述
我们在上面解释了主导Reta 实施的“特许经营”合约[FF]——它与主导Manu 实施的“两部定价”合约具有相同含义。当一个占主导地位的Reta 通过要求执行特许经营费FFR 的[FF]时,他认为Manu 的利润是:
![]()
因为Reta 知道Manu 只有在他的利润至少是ΠMsub 时才会“参与”,所以解决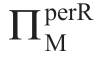 =ΠMsub 给出“β”(即Manu“退出”的关停实际m 值)为:
=ΠMsub 给出“β”(即Manu“退出”的关停实际m 值)为:
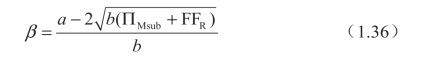
因此Reta 的问题是设定FFR 以最大化:

1.3.4.2 均匀分布结果
引理1.6A 给出了m 服从均匀分布的FFR 表达式。这些表达式清楚地揭示了μm,σm 和ΠMsub 对 的影响。
的影响。
引理1.6A( 表达式)
表达式)
情形 I(σm≤σbF1):
![]()
情形 II(σbF1≤σm≤σbF2):
 (https://www.daowen.com)
(https://www.daowen.com)
分别对应于边界B 和C。
由于较低的 给出了更高的
给出了更高的 ,因此,可以从公式(1.38)和公式(1.39)推导出以下引理1.6B 的结论。
,因此,可以从公式(1.38)和公式(1.39)推导出以下引理1.6B 的结论。
引理 1.6B(μm,σm 和ΠMsub 对 的影响)
的影响)
μm 和ΠMsub 的影响:
随着μm 增加, 总是在降低,因此,随着ΠMsub 增加,
总是在降低,因此,随着ΠMsub 增加, 总是在增加。
总是在增加。
σm 的影响:
情形I:随着σm 增加, 降低(因此
降低(因此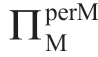 增加)。
增加)。
情形 II:由于“d( )/dσm<0”,因此,
)/dσm<0”,因此, 随着σm 增加而增加(并且
随着σm 增加而增加(并且 降低)。
降低)。
引理 1.6 中μm 和ΠMsub 对 的影响是比较直觉的。令人感兴趣的部分是 σm 对
的影响是比较直觉的。令人感兴趣的部分是 σm 对 的影响:对于[FF]合约,引理 1.6 中的情形 I 至情形III 具有与[U]合约的引理1.5 中的情形Ib、情形II 和情形III 相同的结构,因此,为了简洁起见,我们不会为[FF]合约提供表 1.13 和表 1.14 中的对应表格;然而,作为[U]合约表1.15 的对应表格,在表1.16 中列出了当m 服从伽玛分布(对于其不能获得分析结果)时σm 对
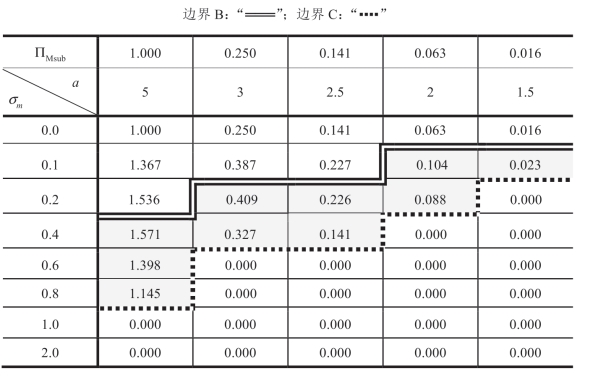
的影响:对于[FF]合约,引理 1.6 中的情形 I 至情形III 具有与[U]合约的引理1.5 中的情形Ib、情形II 和情形III 相同的结构,因此,为了简洁起见,我们不会为[FF]合约提供表 1.13 和表 1.14 中的对应表格;然而,作为[U]合约表1.15 的对应表格,在表1.16 中列出了当m 服从伽玛分布(对于其不能获得分析结果)时σm 对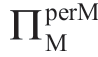 的影响,参数与同表1.15 相同。与上节中[U]合约的发现类似,表1.16 展示了在引理1.6 中分析推导出的均匀分布m 的相同边界B 和边界C。注意,表1.16 中的边界B 位置与表1.15 中的边界B 位置非常相似;即从[U]合约切换到[FF]合约不会改变Manu 或不会被激励他向Reta 提供更好的m 信息的条件。稍后,将在后面小节中看到,同样重要的现象出现在[2P]和[MC]合约中。
的影响,参数与同表1.15 相同。与上节中[U]合约的发现类似,表1.16 展示了在引理1.6 中分析推导出的均匀分布m 的相同边界B 和边界C。注意,表1.16 中的边界B 位置与表1.15 中的边界B 位置非常相似;即从[U]合约切换到[FF]合约不会改变Manu 或不会被激励他向Reta 提供更好的m 信息的条件。稍后,将在后面小节中看到,同样重要的现象出现在[2P]和[MC]合约中。
表1.16a [FF]合约随 a 和σm 变化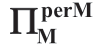 的变化(ΠMsub=0)
的变化(ΠMsub=0)
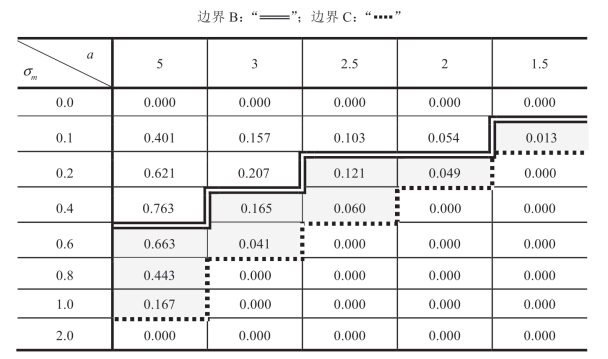
表1.16b [FF]合约随 a 和σm 变化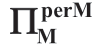 的变化(ΠMsub=
的变化(ΠMsub=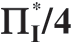 )
)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






