1.3.3.1 基本模型
如果两个参与者都准确地知道mreal,则公式(1.21)和公式(1.22)表示 Reta 将声明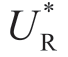 =(a-bmreal)/(2b),Manu 的利润将为
=(a-bmreal)/(2b),Manu 的利润将为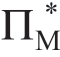 =(a-bmreal)2/(16b)。鉴于当前Reta 只知道m 的分布,我们的最终目的是了解Manu如何影响Reta 的认识m 以增加自己的利润。然而,需要首先获得的中间结果是,当Reta 的m 知识不对称并且只能感知m 时,其应当如何制定最优的价格加成
=(a-bmreal)2/(16b)。鉴于当前Reta 只知道m 的分布,我们的最终目的是了解Manu如何影响Reta 的认识m 以增加自己的利润。然而,需要首先获得的中间结果是,当Reta 的m 知识不对称并且只能感知m 时,其应当如何制定最优的价格加成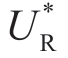 ?
?
当Reta 执行价格加成合约[U]时,给定Reta 设定的UR,Manu 的响应为:
![]()
由于Manu 认为他生产该产品的“名义”利润为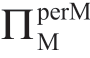 =(w-mreal)(a-bp),其中p=w+UR。将公式(1.24)代入
=(w-mreal)(a-bp),其中p=w+UR。将公式(1.24)代入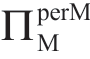 可得:
可得:
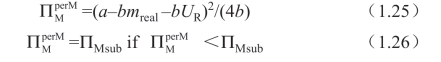
注意:Manu 感知的利润ΠM 和ΠR 与Reta 的感知不同,因此通过上标perM 和perR 来加以区分。对于Reta 给定的任何UR 值,其认为自己的期望利润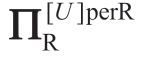 (以下简写
(以下简写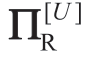 )为:
)为:
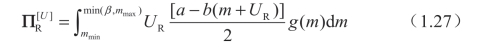
其中:

1.3.3.2 均匀分布结果
对于m 服从均匀分布的情况,在引理1.5A 中给出了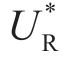 的表达式,引理 1.5B 则表明了μm 和σm 对
的表达式,引理 1.5B 则表明了μm 和σm 对 的影响。1.3 节的所有证明都类似于 1.2.3 节中的证明,为节约篇幅,不再赘述,感兴趣的读者可向作者索要。
的影响。1.3 节的所有证明都类似于 1.2.3 节中的证明,为节约篇幅,不再赘述,感兴趣的读者可向作者索要。
引理1.5A: 的表达式
的表达式
情形 Ia(σm≤σbU1):

情形 Ib(σbU1<σm≤σbU2):
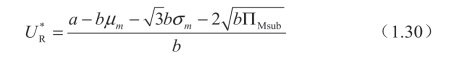
情形 II(σbU2<σm≤σbU3):
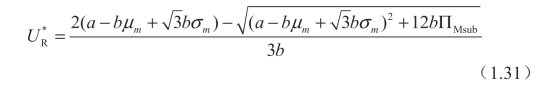
情形 III(σm>σbU3):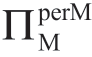 小于ΠMsub,因此交易不发生;
小于ΠMsub,因此交易不发生;
其中:

分别对应于σm 的边界A,B 和C。
引理1.5B:μm,σm 和ΠMsub 对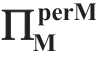 的影响
的影响
μm 和ΠMsub 的影响
对于μm,从公式(1.29)、公式(1.30)和公式(1.31)可以看出,随着μm 增加, 减少;反过来,根据公式(1.25),随着μm 增加,
减少;反过来,根据公式(1.25),随着μm 增加,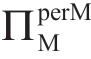 增加。即,Manu 有动机误导Reta 估计一个更大的μm,这也是直观的预期。对于ΠMsub,公式(1.30)和公式(1.31)清楚地表明,随着ΠMsub的增加,
增加。即,Manu 有动机误导Reta 估计一个更大的μm,这也是直观的预期。对于ΠMsub,公式(1.30)和公式(1.31)清楚地表明,随着ΠMsub的增加,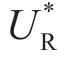 减小,
减小,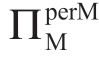 增加。
增加。
σm 的影响
情形Ia: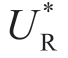 (
(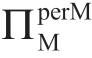 )是关于σm 的常数;
)是关于σm 的常数;
情形Ib: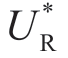 随着σm 增加而减小(
随着σm 增加而减小(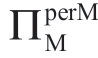 增加);
增加);
情形II: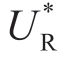 随着σm 增加而增加(
随着σm 增加而增加( 减小)。
减小)。
上述影响表明,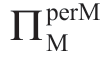 可以被看作是一个σm 拟凹函数。当ΠMsub=0时,σbU1=σbU2;因此,边界A 和B 合并成一个单一的“边界A/B”,情形Ia 和情形Ib 合并成单一的情形I。引理1.5B 的含义在其他部分进行阐述。
可以被看作是一个σm 拟凹函数。当ΠMsub=0时,σbU1=σbU2;因此,边界A 和B 合并成一个单一的“边界A/B”,情形Ia 和情形Ib 合并成单一的情形I。引理1.5B 的含义在其他部分进行阐述。
通过 m 的不确定性 σm 及其偏差(μm-mreal),可以有效地总结 Reta关于m 知识质量的影响。关于偏差,直观上显而易见的是,无论合约格式如何,Manu 都倾向于更大的 μm,因此,1.3.3.3 节将探讨引理 1.5B中体现σm 的影响。
1.3.3.3 σm的影响(https://www.daowen.com)
1. 引理1 的数值解
假设Reta 的m 估计是“无偏的”,即μm=mreal,简化了σm 影响的解释,但是,可以很容易地表明,我们关于σm 影响的结论对 m 偏差估计仍然有效。为了不失一般性,本节中的所有数值例子均设定b=1和mreal=1(因此μm=1)。
2. Manu 的ΠMsub 为 0 的情形
引理1.5 的含义由ΠMsub=0 的表1.1 说明,其中,表1.13a 和表1.13b分别描绘了σm 对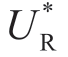 和
和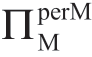 的影响。
的影响。
表1.13a 随a 和σm 变化 的变化,m 均匀分布,μm=1
的变化,m 均匀分布,μm=1
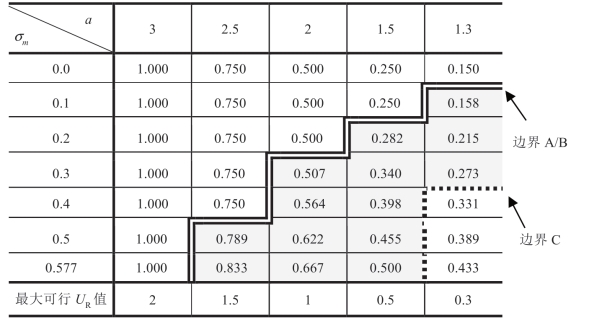
表1.13b 随 a 和σm 变化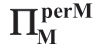 的变化,m 均匀分布,μm=1
的变化,m 均匀分布,μm=1
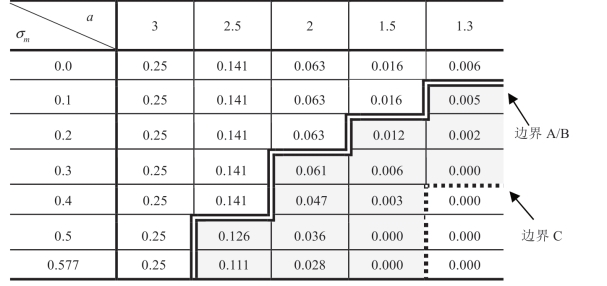
上面两个表中的第一行(σm=0)对应于对称知识的情况。“情形I”对应于双线“边界A/B”的左上方区域,其中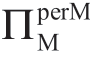 保持不变。“情形II”
保持不变。“情形II”
中Manu 的动机是降低Reta 的σm,对应于边界A/B 和虚线“边界C”之间的右下方灰色区域,不仅a 足够低,而且σm 足够高。从公式(1.16)式中的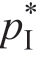 和
和 可以看出,a 的大小反映了产品的潜在收益率。例如,如果 a =2 且μm=1,则
可以看出,a 的大小反映了产品的潜在收益率。例如,如果 a =2 且μm=1,则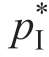 =1.5;即制造成本上的零售价格涨幅是50%——不是很高。换句话说,情形II 对应于Manu 和Reta 都相当于不利的商业环境。事实上,情形II 区域的
=1.5;即制造成本上的零售价格涨幅是50%——不是很高。换句话说,情形II 对应于Manu 和Reta 都相当于不利的商业环境。事实上,情形II 区域的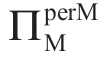 值远低于情景I 区域的
值远低于情景I 区域的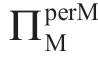 值。从公式(1.31)中可以很容易地确定,由于均匀分布的最大可能的κm 值是
值。从公式(1.31)中可以很容易地确定,由于均匀分布的最大可能的κm 值是![]() 情形II 只能出现在表1.13 中明确描述a<3 的现象。同样,公式(1.19)表明情形III 只有在a<1.5 时才会出现——也如表1.13 所示,因此,除非产品的利润潜力本质上非常低,否则情形I 适用,Manu 不会减少Reta 的感知σm。此外,将在1.3.3.4 节中看到,对于最现实的m 分布,情形Ia 不会出现;即只有情形Ib 适用,因此,Manu 明显有增加σm的动机。
情形II 只能出现在表1.13 中明确描述a<3 的现象。同样,公式(1.19)表明情形III 只有在a<1.5 时才会出现——也如表1.13 所示,因此,除非产品的利润潜力本质上非常低,否则情形I 适用,Manu 不会减少Reta 的感知σm。此外,将在1.3.3.4 节中看到,对于最现实的m 分布,情形Ia 不会出现;即只有情形Ib 适用,因此,Manu 明显有增加σm的动机。
3. 非零的ΠMsub 情形
如1.3.3.2 节所述,当系统参数的知识对称考虑到渠道协调合约(如两部定价合约)时,需要为处于仆从地位的参与者指定非零的ΠMsub,否则该参与者利润将为零。另外,在诸如[w]或[U]之类的纯价格合约下,被支配的参与者不需要非零的ΠMsub 来保证渠道利润的重要份额(见公式(1.17)和公式(1.22))。因此,尽管大多数关于渠道协调合约的研究包含外生固定的非零ΠMsub 值,但大部分早期关于纯定价合约的研究并未假设明确的ΠMsub;或者等价于假设ΠMsub=0。
然而,在本节中,为了比较价格加成合约[U]的结果和后面章节中考虑的渠道协调合约的结果,假设Manu 可能会声明一个非零的ΠMsub。

当Reta 的m 知识不完善时,尽管公式(1.29)表明ΠMsub 的大小在情形Ia 中无关紧要,公式(1.30)和公式(1.31)表明在情形Ib 和情形II 下,更高的ΠMsub 导致更高的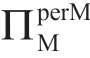 。从一个角度来看,这可能看起来很直观:Manu 变得越苛刻,其得到的就会越多。然而,这与表1.13 和表1.14 中的σm 影响并不完全一致。因此,在情况II 下,虽然Manu 可以通过为 Reta 提供更好的 m 信息(即减少σm);同时,他应该向 Reta提供不太真实的ΠMsub 信息(即夸大ΠMsub)。当然,在情形Ib 中,ΠMsub的作用与σm 的作用一致。也就是说,Manu 的动机是为σm 和ΠMsub 提供不准确的信息,但是,ΠMsub 的效果并不是我们的主要焦点,对其含义的讨论将推迟到后续内容中。
。从一个角度来看,这可能看起来很直观:Manu 变得越苛刻,其得到的就会越多。然而,这与表1.13 和表1.14 中的σm 影响并不完全一致。因此,在情况II 下,虽然Manu 可以通过为 Reta 提供更好的 m 信息(即减少σm);同时,他应该向 Reta提供不太真实的ΠMsub 信息(即夸大ΠMsub)。当然,在情形Ib 中,ΠMsub的作用与σm 的作用一致。也就是说,Manu 的动机是为σm 和ΠMsub 提供不准确的信息,但是,ΠMsub 的效果并不是我们的主要焦点,对其含义的讨论将推迟到后续内容中。
注意,公式(1.26)将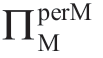 定义为Manu 从考虑的产品或“业务”中获得的利润,因此,当
定义为Manu 从考虑的产品或“业务”中获得的利润,因此,当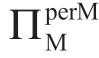 <ΠMsub 并且Manu 拒绝参与时,
<ΠMsub 并且Manu 拒绝参与时,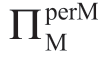 =
=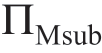 ,因此,它使边界C 在
,因此,它使边界C 在 表中更加清晰(表1.13b 和表1.14)。
表中更加清晰(表1.13b 和表1.14)。
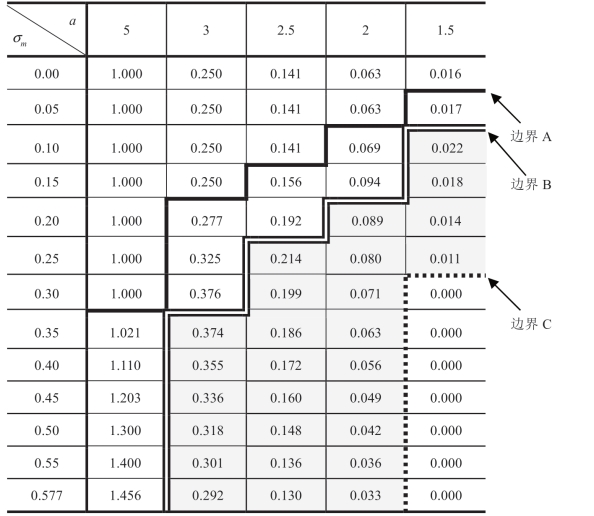
表1.14a 随a 和σm 变化 值的变化,m 均匀分布,μm=1,ΠMsub=
值的变化,m 均匀分布,μm=1,ΠMsub=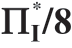
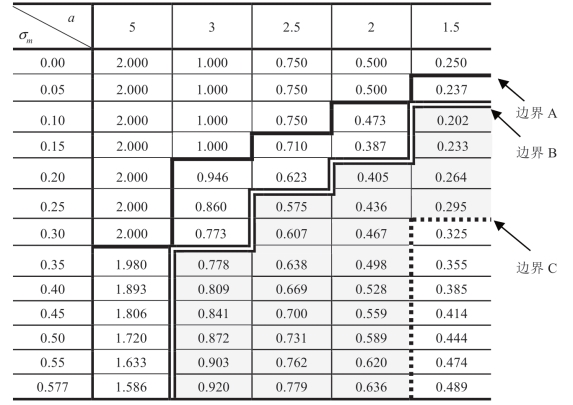
表1.14b 随a 和σm 变化 的变化,m 均匀分布,μm=1,ΠMsub=
的变化,m 均匀分布,μm=1,ΠMsub=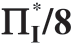
1.3.3.4 伽玛分布情形
引理1.5 的解析结果是通过假设m 为均匀分布来推导的。许多相关研究使用相同的假设来获得解析结果,见Ha(2001)和Corbett 等(2004)等研究。如果 m 遵循无限右尾分布,如正态分布和伽玛分布,则由于mmax=∞,情形Ia 从不适用。不幸的是,如引理1.5A 那样的分析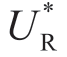 解对于m 为正态,伽玛或威布尔分布时是不可能的。我们用各种无限尾m分布进行了广泛的数值研究,并证实σm 对
解对于m 为正态,伽玛或威布尔分布时是不可能的。我们用各种无限尾m分布进行了广泛的数值研究,并证实σm 对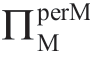 的影响遵循表1.15 中描述的形式。表1.15a 和表1.15b 分别用于ΠMsub=0 和ΠMsub=
的影响遵循表1.15 中描述的形式。表1.15a 和表1.15b 分别用于ΠMsub=0 和ΠMsub=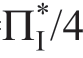 的情况,m 服从伽玛分布且μm=1。
的情况,m 服从伽玛分布且μm=1。
表1.15a 随a 和σm 变化 的变化(ΠMsub=0)
的变化(ΠMsub=0)
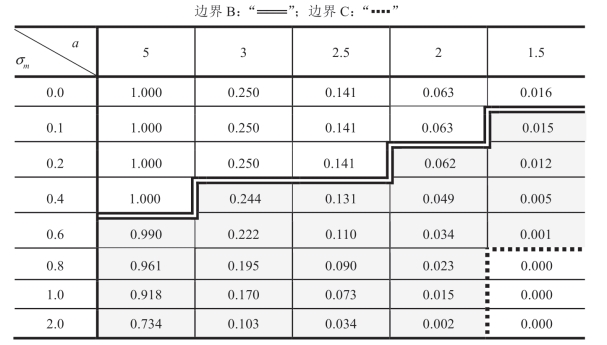
表1.15b [U]中随 a 和σm 变化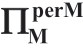 的变化(ΠMsub=
的变化(ΠMsub=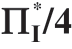 )
)
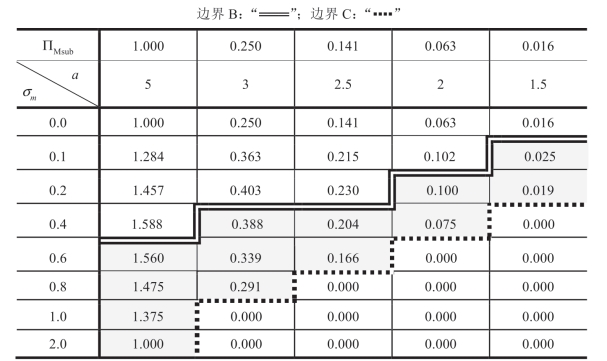
首先,考虑表1.13 和表1.15 具有共同的特征。如在表1.13 和表1.14中,表1.15 还显示边界B 和C 之间的“边界B”和“边界C”,随着σm增加,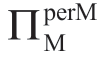 减小。在边界C 下方,
减小。在边界C 下方,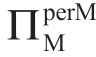 <ΠMsub 并且Manu 拒绝参与。
<ΠMsub 并且Manu 拒绝参与。
现在考虑表1.13、表1.14 和表1.15 之间的差异。首先,对于服从均匀分布的m,公式(1.32)适用于“情形Ia”,并且表1.13b 和表1.14中边界 A 以上的区域说明了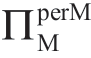 不随着σm 的增加而改变。相反,“情形Ia”不适用于长尾m 分布,因此,表1.15 中没有边界A。请注意,表 1.15a 中边界 B 上方的
不随着σm 的增加而改变。相反,“情形Ia”不适用于长尾m 分布,因此,表1.15 中没有边界A。请注意,表 1.15a 中边界 B 上方的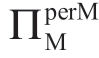 值并非真正保持不变;这些变化太小而无法描述。其次,与表1.13 相比,表1.15 中的边界B 不再局限于“a=3”右侧的区域。最后,与表1.13b 和之前的断言相反,表1.15 中的边界C和情况 III 不再局限于a=1.5 右边的区域。注意,这个特性的启示是由伽玛分布的m 在均匀分布的最大可能κm(0.577) 以上取得一个κm 值的能力促成的。
值并非真正保持不变;这些变化太小而无法描述。其次,与表1.13 相比,表1.15 中的边界B 不再局限于“a=3”右侧的区域。最后,与表1.13b 和之前的断言相反,表1.15 中的边界C和情况 III 不再局限于a=1.5 右边的区域。注意,这个特性的启示是由伽玛分布的m 在均匀分布的最大可能κm(0.577) 以上取得一个κm 值的能力促成的。
因此,虽然用均匀分布假设得到的引理1.5 分析结果提供了有意义的初步见解,但它可能导致最终的错误结论。如从表1.13 和公式(1.29)可以得出结论:在情形Ia 中,相对于σm,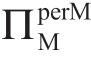 保持不变,而更准确的结论是对于最现实的m 分布,
保持不变,而更准确的结论是对于最现实的m 分布,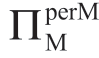 相对于σm 不会保持不变。
相对于σm 不会保持不变。
1.3.3.5 中间总结
总而言之,如果Reta 执行价格加成合约[U],那么Manu 总是会有动机误导 Reta 来感知更高的μm。关于σm,当产品的利润率不太低以及当前的σm 水平不太高时(即表1.15b 中边界B 以上的区域),Manu 有动机增加Reta 的感知σm。从上到下看表1.15b 中任何给定的列(即任何给定的a 值),可以看到Manu 的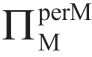 是σm 的单峰函数,并且对于任何给定的a 值,边界B 上σm 值最大化
是σm 的单峰函数,并且对于任何给定的a 值,边界B 上σm 值最大化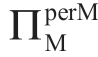 。这些形式在以下各节中分析的其他合约中保持不变。但注意,在我们的情形中,Manu 可以优化的不是σm;Manu 不知道也不能调整 Reta 的σm,尤其当 Reta 意识到 Manu是通过误导他来获益时。
。这些形式在以下各节中分析的其他合约中保持不变。但注意,在我们的情形中,Manu 可以优化的不是σm;Manu 不知道也不能调整 Reta 的σm,尤其当 Reta 意识到 Manu是通过误导他来获益时。
通过假设 Manu 的保留利润ΠMsub,该研究几乎符合所有相关的研究。然而,公式(1.30)、公式(1.31)和表1.15 显示,随着ΠMsub 的增加,被支配的Manu 的利润增加。这确定了一个超出本节讨论范围的问题,但最终还是应该解决:在设计合约时,主导参与者应该如何设置或估计被支配参与者的ΠMsub。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








