本节假设线性需求函数D=a-bp，这是需求D的最普遍形式。为了便于后面的讨论，我们总结了相关的结果。

1.3.2.1 集中决策结果

如果Manu和Reta属于同一个“集成”公司，集成的利润函数可表示为ΠI=(p-mreal)D(p)。众所周知，该公司应该收取的最优单位零售价格以及由此产生的最佳利润分别为：

在本节中的许多符号中，下标“I”“M”和“R”分别表示“集成公司”、Manu和Reta；Π表示“利润”。

1.3.2.2 Manu主导时的渠道结果

如果Manu处于供应链中主导地位，只设定单位批发价w，即采用制造商Stackelberg批发价合约（标记为“[w]”）博弈。设q为市场销售量。已知最佳的合约[w]解决策为：

在本节中，上标[·]标识合约形式，如上面的[w]。结合公式（1.16）和（1.17）中的最优利润表达式给出了[w]下的“渠道效率”（或“CE”）为：

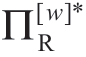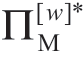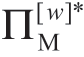占主导地位的Manu可以实施一个“渠道协调”策略，该策略不仅可以使渠道效率CE达到100%，而且还可以任意分配渠道利润，极端情况下，Reta只能获得其保留利润ΠRsub。例如，Manu主导的两部定价合约中（标记为[2P]）（Chopra和Meindl，2004，p. 274），Manu以成本价将产品卖给Reta，但收取Reta的全部利润作为前期特许经营费用FFM；即设定FFM=-ΠRsub和w=mreal。在[2P]下，渠道可以实现渠道协调，获得最大的利润，但Reta只能分得ΠRsub，其余的则转给Manu，然而，在[2P]这样的渠道协调合约下，由于所获得的大于公式（1.17）中所述的（-），即使Manu承诺给予Reta的份额略高于，对他自己而言收益仍然会大于，因此，这种“更大的蛋糕”观点是促进供应链文献中合作和信息共享研究的主要动机。

1.3.2.3 Reta 主导时的结果

有两个方法可供Reta 选择。

方法（i）：作为Manu 占主导地位的[w]合约的镜像，占主导地位的Reta 可以实现的最简单的零售商 Stackelberg 博弈是设定零售商的必要利润率（价格加成）UR——合约形式标记为[U]。下面公式（1.19）～公式（1.22）中总结的结果其更详细解释见Choi（1991）。

在Reta 设定UR 后，每单位零售价格和销售量是：

Manu 的利润函数可写为ΠM=(w-mreal)q=(w-mreal)[a-b(w+UR)]。求解“dΠM/dw=0”得出Manu 的响应函数为：

将w(UR)代入 Reta 的利润函数ΠR=URq 并求解“dΠR/dUR=0”得出最优的价格加成为：

最优决策及相关利润可写为：

公式（1.21）表示，如确定，则Reta 需要知道mreal 才能执行合约[U]，这对本节的研究非常重要。(www.daowen.com)

方法（ii）：类似地，占主导地位的 Reta 也可以实施一个渠道协调策略，该策略不仅可以使渠道效率CE 达到100%，而且也可以任意分配渠道利润，极端情况下，Manu 只能获得保留利润ΠMsub。因此，遵循特许经营合约同样的逻辑，占主导地位的Reta 可以制定以下合约：

也就是说，Reta 宣布不再进行价格加成，但要求 Manu 向她支付FFR= -ΠMsub 的一次性固定费用。由于价格加成等于零，从公式（1.16）和公式（1.20）可以很容易地看出，可以实现渠道协调价格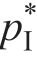，因此，Reta 获得大部分的协调渠道利润，而Manu 只获得ΠMsub。然而，尽管两部制定价合约的名称适用于Manu 主导情形（因为Manu 收取FFM 和非零w），但对于Reta 占主导地位情形是不合适的（因为“第二部分”UR是零），因此，在随后的分析讨论中，称之为“特许经营”合约，标记为[FF]。

根据上面分析，Reta 更倾向于方法（ii）而不是方法（i）。在这种情况下，Manu 获得ΠMsub 而不是，然而，不管实施上面哪一个方法，Reta 都需要完美地了解mreal。

1.3.2.4 成本知识不完美时的结果

如果Reta 完全不了解mreal，那么占主导地位的Reta 可以做什么？对于Manu 占主导地位情形，许多研究都提出或分析了各种合约形式（例如数量折扣合约、两部定价合约），Manu 可以用来增加他的利润，如Corbett 等（2004）。然而，关于Reta 处于主导地位时如何能够协调渠道或提高利润的问题，相关研究很少。基于此，我们将考虑 Reta 可以实施的四种逐渐复杂的合约。

（1）价格加成合约[U]。最简单的合约，Reta 公司只制定价格加成UR。

（2）特许经营合约[FF]。Reta 只征收特许经营费用FFR。

（3）两部定价合约[2P]。除一次性费用LR 外，Reta 还要求收取非零UR。

（4）菜单合约 [MC]。理论上最有利的合约。

合约（1）、（3）和（4）对应于Corbett 等（2004）研究的三种Manu占主导地位时的合约。对于这四种合约，首先，我们将调查Manu 的利润如何受到Reta 的m 知识“质量”的影响；其次，利用这些中间结果，分析最终的问题，即Manu 是否希望提高Reta 的m 知识质量。注意，在信息不对称的情况下，使渠道效率最大化的[2P]合约与最大化主导企业期望利润的[2P]合约不同。在本文中，假设主导的Reta 将设计合约以最大化他的期望利润。

将Reta 对m 的不确定知识作为一个主观随机变量m，其概率密度函数为g(m)，分布函数为G(m)，均值为μm，标准差为σm，支持区间为（mmin，mmax）。κm 代表 m 的变异系数（σm/μm）。Reta 的 m 知识“质量”将体现在：（i）不确定性，或者σm；（ii）偏差，即（μm-mreal）。

正如将要看到的那样，我们将考虑m 服从均匀分布情形（解析结果）和服从伽玛分布情形（数值结果）。利用均匀分布，能够获得有关μm 和σm 对 Manu 利润影响的解析结果。对于伽玛分布，σm 的影响将采用数值解表示（μm 的影响不需要进一步展示）。从前面小节的结果得出的基本结论是：在四种合约中，Manu 的利润随着m 的偏差（或μm）的增加而增加（这在直觉上是显而易见的）。此外，一般条件下，Manu 的利润随着Reta 对m（即σm）不确定性的增加而增加，因此，即使σm 或（μm-mreal）降低可以提高 CE（渠道效率），但实现更高的渠道效率可能不是激励Manu 与Reta 分享m 知识的有效因素。另外，我们也得到了一个间接结果：主导者Manu 会通过夸大其保留利润水平ΠMsub 来增加利润。

1.3.2.5 两种随机成本分布形式

在许多相关研究中，广泛采用m 服从均匀分布（如Ha，2001）。针对均匀分布，有以下结果：

均匀分布有一个厚的截断右尾，其κm 是有限的，最大值只有0.577，因此，为了模拟具有较高κm 和较长右尾的m，我们还考虑了 m 服从伽玛分布，其概率密度函数为：