1.2.5.1 Reta对信息精确度σc的偏好

我们遵循前两节中使用的方法。首先，对于c服从均匀分布的情况（即对应的引理1.1～引理1.4），能够获得类似于情形a的解析解，也获得了c服从伽玛分布情况下的数值解，它不仅比均匀分布c解析解显示出更多的特性，而且更容易理解。由于a和b的早期结果有许多共同之处，为简洁起见，将省略[FF]数值结果。因此，表1.10，表1.11和表1.12分别对应于前一节中[w]、[2P]和[MC]的表1.1、表1.4和表1.5。下文指出了与先前a和b所得结果的不同之处并强调了这些差异。

表1.10　批发价合约（[w]）下的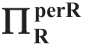

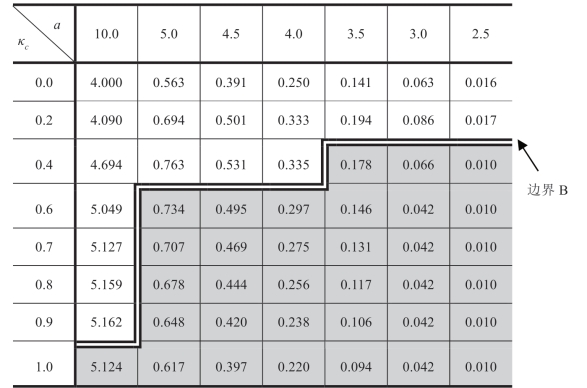
注：c服从伽玛分布，μc=1，b=1，ΠRsub=[a-b(μc+m)]2/(24b)。

表1.11　两部定价合约（[2P]）下的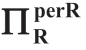

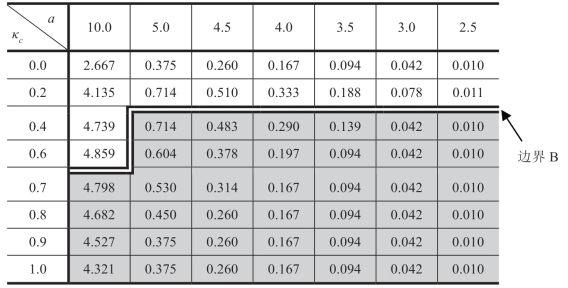
注：c服从伽玛分布，μc=1，b=1，ΠRsub=[a-b(μc+m)]2/(24b)。

表1.12　菜单合约（[MC]）下的

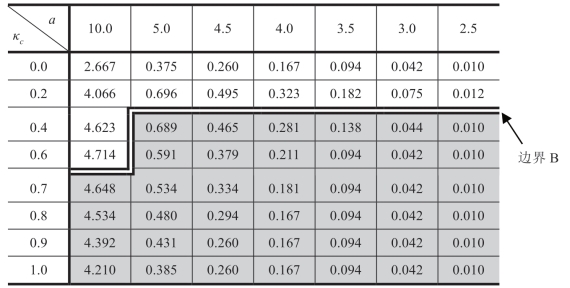
注：c服从伽玛分布，μc=1，b=1，ΠRsub=[a-b(μc+m)]2/(24b)。

到目前为止，表1.10～表1.12和前面的表格之间的以下相似之处应该是显而易见的：

（1）有一个情形I（情形II）区域，其中κc足够低（高），并且Reta喜欢Manu对c所知更加（少）不确定。低或高κc区域在数字表格中用“边界B”（线条“”）图形分隔。(www.daowen.com)

（2）当Manu的合约从最简单的格式（即[w]）变为最复杂和最强大的格式（即[MC]）时，边界B的位置没有实质性变化。

这部分c不确定性结果（表1.10～表1.12）与较早的a和b不确定性结果（表1.2至表1.9）之间的显著差异在于边界B所处的κ值大小。总之，现在情形I区域比a和b中的不确定性更为普遍。详细说明一下，以表1.10中a=5.0列为例。如前所述，从公式（1.2）得到pI*=[a+b(μc+m)]/(2b)=(5+2)/2=3.5，并且成本加成标记为M=(pI*-k)/k=0.75。即，这里的盈利能力与表1.2中c=1.0的列相同。然而，表1.2的“c=1.0”列中的边界B出现在κa=0.13附近，而表1.10的“a=5.0”列中的边界B出现在κc=0.5附近。注意到均匀分布随机变量可能的最大κ值为0.577，κc=0.5时的边界B位置，意味着情形I（边界B以上的区域）在c的不确定性水平中占很大比例。表1.10中“a=5.0”右边的列表示不太可能发生的低利润率条件。向左移动，表1.10中的“a=10.0”列对应于成本为2的加成M不是不现实的高值，然而，针对这个M值，情形II直到κc=0.95时才会出现，因此，与前面各节对a和b所得出的结论相反，表1.10表明，当Manu对c的认识有不确定性时，则在大多数合理的条件下，Reta被激励，诱导Manu相信c具有更高的不确定性。

表1.10显示了在本书中考虑均匀分布和伽玛分布的必要性，即在某些值的情况下，只有当κc超过0.577时才会出现“情形II”，由于仅使用均匀分布不能充分说明情形II，因此，为了便于直接比较，表1.2～表1.12全部使用伽玛分布进行数值分析。

在表1.11和表1.12中，边界B比表1.10中的位置略高，然而，它不改变前文基于[w]和基于a和b不确定性得出的结论：

（1）在一系列合理的条件下（情况I），Reta更喜欢Manu对c更加不确定。另外，Manu不能通过使用更复杂的合约格式（如[MC]）而不是更简单的合约格式（如[w]）来显著缩小或改变情形I的范围。

（2）与需求的不确定性（即 σa和 σb）相反，在 c 具有不确定性的情况下，情形I比情形II更为普遍。

1.2.5.2 Reta对信息倾向μc的偏好

Reta总会试图诱导Manu感知更高的μc（见图1.4）和更高的ΠRsub，这是直观明显并容易证明的。

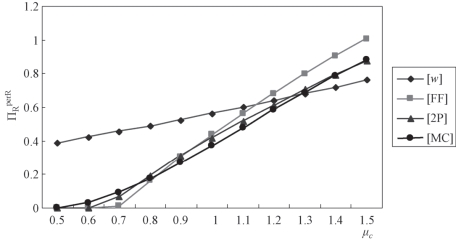
图1.4　c服从伽玛分布，σc=0.4，creal=1，a=5，b=1，ΠRsub=0

考虑公式（1.1）和公式（1.2）中给出的利润函数和需求曲线定义的非常基本的两级供应链系统。在最初阶段（图1.1中的时刻A），主导制造商（Manu）对系统参数（a，b，c）的值具有随机感知，但未指定供应合约。我们调查零售商希望Manu如何感知（a，b，c）以及Reta是否（或可能）有动机提高Manu的感知质量。最直观明显的结果是：Reta总是诱导Manu来感知一个较大的μc值和一个较大的ΠRsub。一个不太明显的结论是，Reta总是被动诱导Manu来感知一个较小的μa值和一个较大的μb值（这既不反直觉也不直观）。我们最直截了当的结果是，在合理条件的范围下，Reta的动机是增加Manu对（a，b，c）感知的不确定性水平（σ）。此外，通过在时刻B使用（或威胁使用）更复杂的合约格式（如“菜单合约”），不能缩小这种引起混淆的条件范围。

最后的结果（关于Reta的σ偏好）可以从两个方面查看。一方面，当前对供应链协调的重视可能会促使人们“猜测”理性的Reta想要提高Manu对（a，b，c）的感知质量（即降低σ），特别是即将实施的是协调激励合约；另一方面，信息租金的原则可能会促使人们“猜测”Reta不愿意免费帮助Manu。结果表明，这两种猜测都是对的。因此，人们可以争辩说，一个协调驱动的合约对激励Reta减少（a，b，c）上Manu的σ没有任何影响。从相反的方向看，人们也可能会认为，存在一系列的条件使Reta很有兴趣改善Manu的σ，这显然是“免费的”。