1.2.4.1 Reta对信息精确度的偏好

本节遵循1.2.3.5节中使用的方法，并计算了参数b服从伽玛分布的情况下的多组数值解，但是，与a情况相反，我们无法针对b服从均匀分布的情况（即对应引理1.1A/1.2A/1.3A/1.4A）获得解析解。幸运的是，数值解所揭示的行为形式大体上与1.2.3.5中的a相同。

因此，为了简洁起见，我们仅列出表 1.6～表 1.9，这些表格是表 1.2～表1.5（前面考虑的a）的对应表格。

表1.6　批发价合约（[w]）下的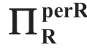

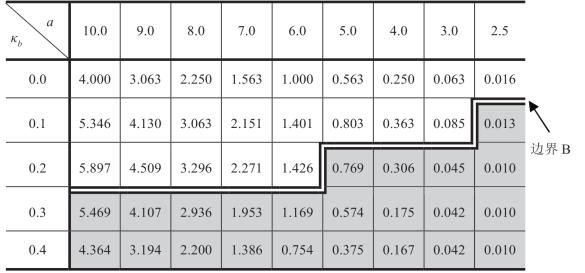
注：b 服从伽玛分布，μb=1，c=1，ΠRsub=(a-μbk)2/(24μb)。

表1.7　特许经营合约（[FF]）下的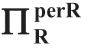

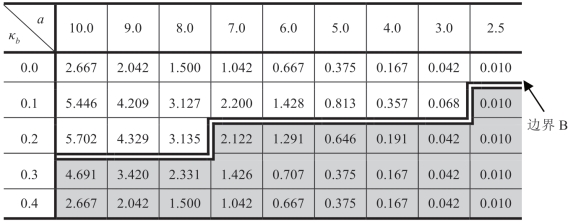
注：b 服从伽玛分布，μb=1，c=1，ΠRsub=(a-μbk)2/(24μb)。

表1.8　两部定价合约（[2P]）下的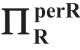

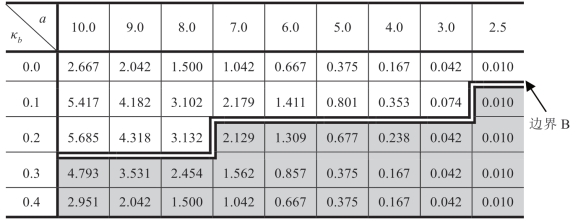
注：b 服从伽玛分布，μb=1，c=1，ΠRsub=(a-μbk)2/(24μb)。(www.daowen.com)

表1.9　菜单合约（[MC]）下的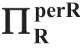

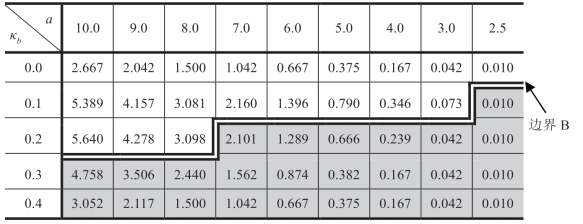
注：b 服从伽玛分布，μb=1，c=1，ΠRsub=(a-μbk)2/(24μb)。

关于σb的表1.6～1.9描述的以下结论与上节中关于σa的描述基本相同：

（1）在一系列合理的条件下（情形I），Reta更偏好Manu对b更加不确定。然而，情形I看起来不像情形II那样普遍（在此情况下，Reta更喜欢Manu对b不确定），然而，这一结论在下节中与“c”的知识不确定性被认为是矛盾的。

（2）Manu不能通过使用更复杂的合约格式（如[MC]）而是通过简单的合约格式（如[w]）来显著缩小或改变情形I的范围。

1.2.4.2 Reta对μb和ΠRsub的偏好

引理1.1A第二部分中的w*表达式表明，随着μa的减小，w*减小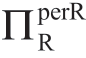（ 增加），因此得出结论“当Manu采用[w]时，Reta总是偏好较低的μa”，然而，引理1.1A中w*表达式没有导出μa的影响，它们是为了揭示σa的作用这个更为困难的目标而得出的。如果只需要μa的影响，就可以简单地观察w*=(a+bk)/(2b)，这清楚地表明w*随着a（或μa）的减少而减小。在研究不对称信息b（而不是a）时，引理1.1A不能得到类似于的关于σb影响的解析表达式，而如果只需要分析μb的影响就变得非常容易。例如，随着b的增加，w*减少（因此增加）。因此，当Manu实施[w]时，Reta总是偏好较高的μb。对于[FF]、[2P]和[MC]，可以得到同样的结论，如图1.3所示。

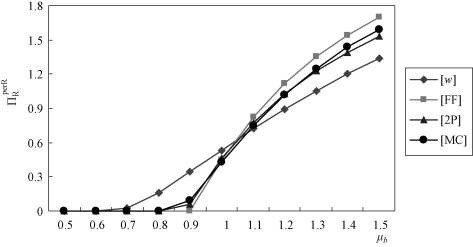
图1.3　b服从伽玛分布，σb=0.2，breal=1，a=5，c=1，ΠRsub=0

综上所述：Reta总是试图误导Manu感知到尽可能高的μb值。类似地，可以很容易地表明Reta总是偏好Manu感知高的ΠRsub值。