在1.2.3.1节中，我们考虑当双方都知道Manu提供批发价合约时，Reta将如何分享其私人a知识信息，然后，在1.2.3.2节至1.2.3.4节中，我们将考虑当双方知道Manu提供特许经营合约（[FF]）、两部定价合约（[2P]）和菜单合约（[MC ]）时，Reta将如何分享其私人的a知识信息。在每一种合约下，首先，我们列出了Manu对参数“a”的先验主观知识服从伽玛分布时的数值结果，说明在本章中的主要结论；其次，当Manu对参数“a”的先验主观知识服从均匀分布时，能够推导出的解析结果进一步证实了该结论（在1.2.3.5小节详细地给出了伽玛分布时的数值结果）。

研究结果表明：

（1）Reta将降低μa（如图1.2所示，在四种合约下，是μa的递减函数）；在一个合理的条件范围下（σa较小时），Reta希望Manu的σa越大越好（ 是σa的拟凹函数）； （2） Manu不能通过实施（或威胁实施）更复杂的合约格式（如[MC]）而是通过更简单的一个（如[w]）来缩小或调整这种引起上述结果的条件范围。

图1.2　a服从伽玛分布，σa= 0.4，areal = 5，b = 1，c =1，ΠRsub = 0

1.2.3.1 批发价合约[w]

问题描述

因此，Manu设定最优的单位批发价为w*，其中w*是问题（1.5）的解。然后，从 Reta 的角度看，如果Manu只能用分布函数F(a)来估计a值，则 Reta 的利润（Reta知道真实的a值，自己感知的利润）是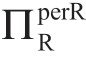=[areal-b(w*+c)]2/(4b)。该式表明，较低的w*带来较高的，因此，Reta问题是：什么样的Manu知识F(a)会导致较低的w*，因此，产生更高的？下面先采用数值结果（表1.2）来说明，然后再解析证明。

数值结果

表1.2　批发价合约([w]）下的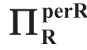

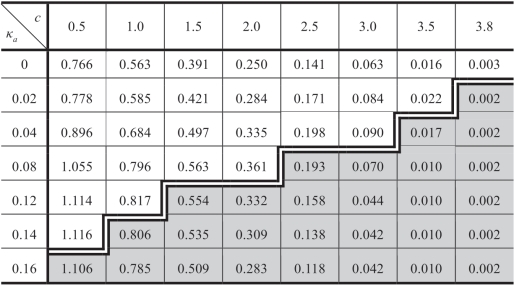
注：a服从伽玛分布，μa=5，b=1和ΠRsub=(μa-bk)2/(24b)。

表1.2给出了c值和κa值（或等同于σa值）不同组合下的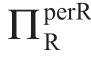值；注意κx ≡ x的变异系数。其他参数的值设置为：areal=μa=5。为了不失一般性，在本章中设定m=1。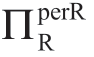值是通过数值求解问题（1.5）得到w*，然后计算=[areal-b(w*+c)]2/(4b)。表1.2显示，对于任何给定的c值（即沿着每个c列），在σa“足够大”的较低（灰色）区域，随着σa增加而减小，但是在σa“足够小”的上部（非灰色）区域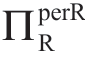，随着σa增加而增加。换句话说，在一系列合理的条件下（也就是说σa比较低时），Reta是希望增加Manu对a的不确定性，即信息优势的增加对Reta有利；然而，当σa大过一临界值（图中的边界B）时，信息优势的增加反而对Reta不利。也就是说，是σa的拟凹函数（Quasi-Concave）。使用参数μa，b，m和ΠRsub值的不同组合重复计算表1.2，结果证实了表1.2所示的形式。

解析证明

表1.2中描述的行为也可以在附录A1中以a为均匀分布的情况导出，主要结果归纳为引理1.1A到1.1C。

引理1.1A（Manu的最优w决策）

其中，σaWA，σaWB和σaWC定义见附录A1.1中的公式（A1.6）、公式（A1.9）和公式（A1.10）。

由于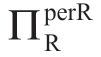随着w的减小而增加，通过观察上面引理1.1A中给出的w*表达式，很容易得到以下结论：

引理1.1B（σa对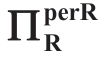的影响）

在情形Ia中，w*和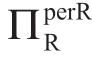 独立于σa；

在情形Ib中，随着σa的增大，w*减小，从而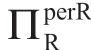R增大；

在情形II中，随着σa的增大，w*增加，因此减小。

类似地，可以得出其他参数的影响。

引理1.1C（μa和ΠRsub对的影响）

μa的影响：在所有情况下，随着μa的增大，w*增大，即随着μa增加而降低；因此，Reta总是有动机诱导Manu感知更小的μa。

ΠRsub的影响：在所有情形下，随着ΠRsub的增加w*减小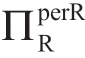，增加；因此，Reta总是有动机说服Manu承认一个较高的ΠRsub。

讨论

虽然本章不打算考虑ΠRsub，但引理1.1C中的ΠRsub的影响是值得注意的。一方面，引理1.1C中ΠRsub的影响比较直观明显；另一方面，以前考虑ΠRsub的模型总是假设Manu知道并接受ΠRsub。引理1.1C表明设置ΠRsub是一个值得深入研究的问题。现在回到主要问题：Manu的a知识。衡量Manu的a知识质量的两个重要指标是：（i）a的偏差测度（μa-areal）（信息倾向）；（ii）a的不确定性测度：σa（信息精度）。如果σa=0（无不确定性）并且μa-areal=0（无偏），则Manu的a知识是完美的。

1. Reta对信息倾向μa的偏好

一个更高的a值意味着更高的“基本需求”，因此，引理1.1C的结果意味着Reta总是试图误导Manu进入尽可能低的μa值。这既不是反直觉的，也不是直观明显的。一个处于仆从地位的参与者会希望主导参与者（如“老板”）把操作环境看得比实际更“艰苦”一点也就不足为奇了。另外，最近的一些模型（例如，Chu和Lee，2006）已经表明Reta更倾向于传输高需求信号——这些模型涉及产能和需求不确定性因素，这些在本书考虑的简练模型中是不存在的。

2. Reta对信息精度σa的偏好

与μa的效果相反，我们的结果表明，σa（等价于κa）的影响是非常反直觉的。引理1.1B表明， 是一个关于σa的拟凹函数，在σaWB上达到最大值。当然，σa（或κa）的影响由表1.2图解说明，其中边界B下方的灰色区域（线“”）对应于情形II，边界B上方的白色区域对应于Ib，这从附录A1.1的推导中可以很容易地看出。如果参数a的概率分布有一个长的右尾部（如伽玛分布），则结果如表1.2那样，不显示情况Ia区域——与引理1.1均匀分布时的结果不同。对情形Ib，Reta偏爱Manu的σa较高，即与其分享自己的a信息，但实际动机是混淆Manu的a知识，这违背了日益流行的供应链互惠互利信息共享的概念。尽管如此，表1.2还描述了情形Ib区域总是高于情形II区域；即当σa“太低”时，Reta被激励增加σa，但是当σa“太高”时要减少σa，因此，σa反直觉的影响在“一切都是适度的”这一很有吸引力的概念是符合直觉的。

现在研究情形I区域相对于情形II区域有多大。考虑均匀分布的情况，将κaBB定义为边界B的κa值。假设ΠRsub=0，公式（A1.9）表示为：

即κaBB应小于或0.29。表1.2描述了对于具有非零ΠRsub和a服从伽玛分布（而不是均匀）的情况，κaBB值显著小于0.29；因此，对于表1.2，当c=1时，κaBB ≈ 0.12。在此c值下，假设μa=areal，公式（1.3）给出pI*=(areal+bk)/(2b)=(5+2)/2=3.5，其中k=m+c=2，因此，考虑到这是Manu和Reta的合并毛利率，理论上的最优加价成本是M=(pI*-k)/k =0.75，接近实际M值的下限，因此，表1.2中“c=1”列右边的列表示不太现实的条件，因为它们没有足够的盈利能力，而表1.2中“c=1”列左侧的列表示越来越有利可图的条件。换句话说，对于系统参数值的大多数实际组合，当κa介于0和（非常粗略）0.2之间时，“情形I”适用，因此，虽然情形I并非完全可以忽略不计，但它可能没有情形II那样普遍，然而，这一结论将在1.2.3.5中与“c”中的知识不确定性放在一起考虑。

1.2.3.2 特许经营合约[FF]

问题描述

在合约[FF]下，Manu向Reta收取一次性费用FFM，并以成本价提供产品给后者，即每单位产品成本m。如果Manu知道市场需求规模a，那么他就可以从公式（1.3）中看出Reta的利润为：

由于Manu知道，只有当Reta的利润至少是ΠRsub时，才会“参与”，求解“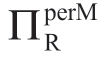=ΠRsub”问题并给出“β”（如果a值低于该值，Reta将退出交易）：

因此，Manu的问题在于如何设定FFM实现利润最大化：

从Reta的角度来看，如果Manu收取FFM，则其利润（如其所感知的）是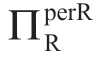=(areal-bk)2/(4b)-FFM。Reta更喜欢能使FFM更低的Manu的信息估计F(a)，从而获得更高的。

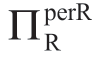数值结果

表1.3　特许经营合约（[FF]）下的

注：a服从伽玛分布，μa=5，b=1，ΠRsub=(μa-bk)2/(24b)。

作为与表1.2对应的表格，表1.3给出了当a服从伽玛分布时，[FF]下不同c值和κa值（或等效的σa值）组合下的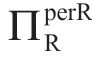值。其他参数（即μa，b，m和ΠRsub）的值如表1.2所示。表1.3描述的σa对 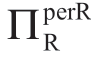的影响与表1.2所示的非常相似。“边界B”（标记为“”）在从表1.2移动到表1.3时大致保持不变，即实施合约[FF]而不是[w]，不改变或缩小Reta偏好Manu信息精度σa的范围。

解析证明

表1.3中描述的行为（以及其他影响）也可在a服从均匀分布的条件下分析推导出，见附录A1.2。主要结果总结为引理1.2A～1.2C；它们与1.2.3.1节[w]中给出的引理1.1A～1.1C并列。

引理1.2A（Manu的最优FFM决策）

根据不同“情形”，Manu的为：

情形I（σa≤σaFB）：

情形II（当σaFB＜σa≤σaFC）：

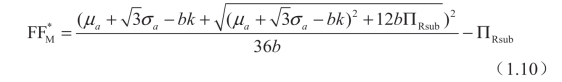(www.daowen.com)

情形III（σa＞σaFC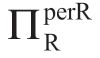）：小于ΠRsub，因此交易不发生。

其中，临界值σaFB和σaFC的定义见附录A1.2中的公式（A1.15）和公式（A1.16）。

由于上面结果显示，当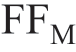减小时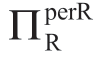，增加，通过观察上面引理1.2A中给出的FFM表达式，很容易得到以下结论：

引理1.2B（σa对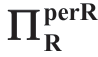的影响）

情况I：随着σa增加， 减小，因此增加；

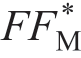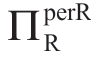情况II：随着σa增加， 增加，因此减小。故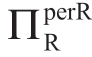， 是σa的一个拟凹函数，其最大值点为σaFB。

引理1.2C（μa和ΠRsub对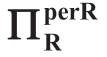的影响）

μa和ΠRsub对[FF]下的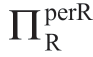的影响与[w]合约的引理 1.1C 中所述的相同。

1.2.3.3 两部定价合约[2P]

问题描述

在两部定价合约[2P]下，Manu向Reta收取一笔总费用L，并以单位批发价w出售商品。类似于[w]和[FF]中给出的论点，[2P]下的Manu问题可以表示为：

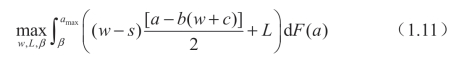
数值结果

表1.4　两部定价合约（[2P]）下的

注：a 服从伽玛分布，μa=5，b=1，ΠRsub=(μa-bk)2/(24b)。

作为表1.2和表1.3的对应表，表1.4列出了当a服从伽玛分布时，两部定价合约[2P]中c和σa值不同组合下的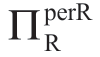值。同样，表1.4描述的σa对的影响与表1.2和表1.3中描述的非常相似，并且在1.2.3.2中对[FF]给出的分析也适用于此。

解析证明

表1.4中描述的行为（以及其他影响）也可以在a服从均匀分布时导出，见附录A1.3。主要结果总结为引理1.3A～1.3C；它们与1.2.3.1[w]中给出的引理1.1A～1.1C和在1.2.3.2节[FF]中给出的引理1.2A～1.2C并列。

引理1.3A（[2P]合约下Manu对w和L的最优决策）

根据不同“情形”，[2P]合约下，Manu对于w和L的最优决策为：

情形I（σa≤min(σaTA，σaTB)）：

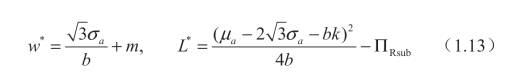
情形IIa（min(σaTA，σaTB)＜σa≤σaTB）：

情形IIb（σaTB＜σa≤σaTC）：

情形III（σa＞σaTC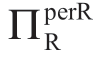）：小于ΠRsub，因此交易不发生。

其中，临界值σaTA，σaTB和σaTC的定义见附录A1.3中的公式（A1.30），公式（A1.27）和公式（A1.31）。

引理1.3B（σa对的影响）

情形I：随着σa增加而增加；

情形IIa和IIb：随着σa增加而减小。因此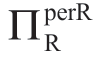，是σa的拟凹函数，其最大值点在min(σaTA，σaTB)。

引理1.3C（μa和ΠRsub对的影响）

在[2P]合约下，μa和ΠRsub对的影响与[w]和[FF]合约的引理1.1C和1.2C中所述相同。

1.2.3.4 菜单合约[MC]

菜单合约（[MC]）格式的简要说明

正如Myerson（1979），Ha（2001）和Corbett等（2004）的解释，Manu有可能指定函数w(adec)和L(adec)，强迫Reta将真实的a值声明为adec，并且 [MC]能给Manu提供给定随机a知识状态下的最高期望利润。

数值结果

表1.5　菜单合约（[MC]）下的

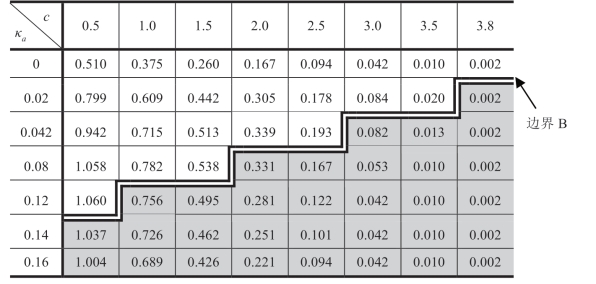
注：a服从伽玛分布，μa=5，b=1，ΠRsub=(μa-bk)2/(24b)。

作为表1.2～表1.4的对应表，表1.5给出了当a服从伽玛分布时，[MC]中c和σa值不同组合下的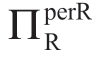值。同样，表1.5描述的σa对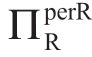的影响与表1.2～1.4中描述的非常相似，并且在上述章节中对[FF]和[2P]所做的结论在这里也适用。

解析证明

表1.5中描述的行为（以及其他影响）同样可以在a服从均匀分布时推导可得，见引理1.4。引理1.4证明见附录A1.4，其中详述了“引理1.4A”的实质（即与引理1.1A，1.2A和1.3A相对应）。下文所述的引理1.4B至1.4C是前面引理1.1B/1.1C，1.2B/1.2C和1.3B/1.3C的对应。

引理1.4B

根据不同“情形”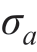，对Reta的的影响为：

情形I（σa≤min(σaMA，σaMB)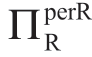）：随着σa增加而增加；

情形IIa（min(σaMA，σaMB)＜σa≤σaMB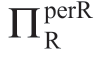）：随着σa增加而降低；

情形IIb（σaMB＜σa≤σaMC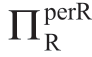）：随着σa增加而降低；

情形II（σa＞σaMC）：小于ΠRsub，因此交易不发生。

其中，临界值σaMA，σaMB和σaMC的定义参见附录A1.4中的公式（A1.47），公式（A1.45）和公式（A1.48）。

引理1.4C：

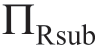随着μa的增加而降低，随着的增加而增加。

1.2.3.5 非对称信息a情形的总结与讨论

从1.2.3.1～1.2.3.4，每个小节都表明，考虑Reta已经知道Manu将使用的合约格式（无论是[w]、[FF]、[2P]还是[MC]），当Manu试图确定供应合约的参数值时，Reta更喜欢Manu的a不确定性更高的“情形I”条件集。据了解，[w]（[MC]）是Manu可能实施的最简单（最复杂的）供应合约格式，因此，由于不同合约格式的情形I范围基本保持不变，因此，综合第1.2.3.1～1.2.3.4 小节可以使我们得出结论：即使Reta不知道Manu将使用什么样的合约格式，仍然有一个大致恒定的条件集合，当Manu制定供应合约时，其更喜欢Manu对a不太确定；然而，正如上面所解释的那样，这些情形I条件并不比情形II情况更普遍。此外，Reta总有动机诱导Manu相信ΠRsub较大，而μa较小。

这里提出的分析推导和数值计算是在Reta完美地知道a的假设下完成的，然而，可以很容易地表明，如果假设Reta只知道一个随机变量a′（这可能与Manu感知的a不同），那么也可以得到相同的结论。例如，在[w]中，公式（1.4）给出了Reta的期望利润，E[]=E[a′-b(w*+c)]2/(4b)，很明显，较低的w*导致较高的E[]。将这个结论与引理1.1A相结合，再次得出引理1.1B。相同的论点适用于引理1.2和引理1.3（对于[FF]和[2P]），因为Manu意识到Reta只知道一个随机变量，现在必须推导出一组不同的[w(adec)，L(adec)]，所以[MC]提出了更大的困难。这是因为，与[w]、[FF]和[2P]不同，Reta的知识在Manu的[MC]设计中扮演着重要角色。

换句话说，通过扩展，结果可以很容易地被证明，无论Reta是否完全了解参数（如a），在[w]、[FF]和[2P]下都存在“情形I”，其中Reta更偏好Manu对a不确定。尽管[MC]的分析结果不能类似地扩展，但似乎有理由将相同的结论推测扩展到[MC]。换句话说，存在一个“情形I”，在这个情形下，无论Reta对自己的a知识如何，Reta都偏好Manu的σa更大。