为了调查上面的问题，我们考虑了由一个占主导地位的制造商（以下简称“Manu”）和一个处于仆从地位的零售商（以下简称“Reta”），然而后者具有市场参数（在线性需求函数“a - bp”中的市场规模a或市场敏感度b）或成本参数（Reta的加工成本c）的私有信息。Manu将不对称参数看作一个服从分布F(·)的随机变量，其相关符号定义见表1.1。

表1.1　符号定义

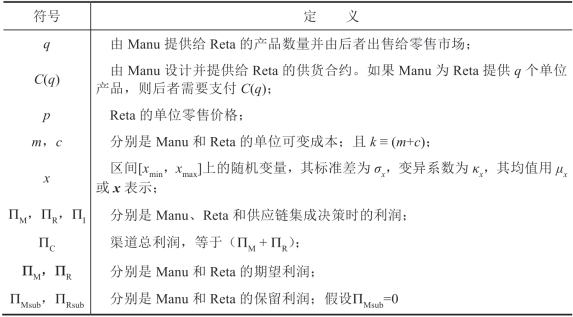
给定由Manu设计的合约C(q)和由Reta制定的决策q和p，Manu和Reta的利润分别为：

Reta知道对于任何他设定的价格p，市场需求都是由线性需求曲线决定：

在这个模型中，Reta的决策变量是（q和p），Manu的决策是C(q)的格式和C(q)的参数值。Manu的环境变量分别为m，a，b和c。为简化分析，没有考虑制造能力、生产交付时间、物流成本和预测，以及Reta需求不确定性、信息传输成本等因素的约束，因此，已经尽可能地去除了干扰Reta隐藏其优势知识a，b和c的因素，目的是减少与问题没有直接关系的因素造成的混杂效应，让目光聚焦于我们关注的问题上。

决策或行动顺序如图1.1所示。在时刻A，Reta能够预见到他提供的信息对Manu设计的供应合约C(q)条款产生的影响，其将设法操纵Manu的信息知识，以便最大化其利润。Reta想知道在时刻A有关参数a（或b，或c）的信息水平对其有什么好处。公式（1.1）中的利润函数假定Manu和Reta有足够的时间来调整运作，使由Manu生产的所有产品和Reta订购的产品都将被出售。

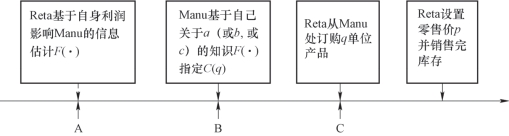
图1.1　显示时间点A，B和C的行动序列(www.daowen.com)

考虑以下四个Manu设计的供货合约C(q) 格式（按“复杂程度”的顺序排列）：

（1）批发价合约，标记为[w]，这是最简单的C(q)格式。Manu从Reta处收取单位产品批发价w。

（2）特许经营合约（Franchise Fee），标记为[FF]。Manu要求Reta支付特许经营费用FFM，然后他以成本价(即每单位m)向Reta提供该产品。

（3）两部定价合约（Two-Part Tariff），标记为[2P]。Manu要求Reta支付一次性费用L和单位产品批发价w。

（4）菜单合约（Menu of Contracts），标记为[MC]。假设目前Manu确定地知道除a外的所有参数，[amin，amax]是Manu感知参数a的主观概率分布区间。Manu的[MC]格式为{[w(adec)，L(adec)]|amin≤adec≤amax}，即Manu告知Reta，如果Reta公司宣布市场规模a值为adec，Manu将会在单位批发价w(adec)的基础上加收一次性付款L(adec)作为转移支付。即，w(adec)和L(adec)是adec的函数。Myerson（1979）和Ha（2001）等人已经证明，对于给定Manu初始的随机a知识，Manu可以设计包含w(adec)和L(adec)的合约，Reta就会在图1.1中的时刻C处声明自己的实际a值为adec；所得到的[MC]则让Manu获得高于其他任何合约所能获得的期望利润。同样，如果Manu确定地知道除b或c以外的所有参数，则Manu的[MC]格式将分别为：

以上四种合约形式中，菜单合约应是最受Manu欢迎的合约格式。当然，除了这四种合约之外还有其他的格式，但这四种合约已足以支持我们将在本章中得出的结论。

为了使分析结果更容易处理，我们通过均值和方差（如μa和σa2）进一步对信息感知（估计）F(·)建模，用均值表示信息倾向和方差表示信息精度（噪声）。当均值等于实际值时，Manu的信息被认为是无偏的，我们将研究Reta会让不知情的Manu拥有什么样的信息倾向和精度。

关于信息倾向，在实践中很常见。Fisher（2007，p. 375）曾与一家大型公司的制造部门合作，该公司跟踪了销售和市场部门编制的预测，发现他们的预测超过了实际需求30%。Terwiesch等（2005）也观察到了定制生产设备的买方与一组设备供应商之间的预测膨胀现象。在本章中，预测膨胀可以理解为“随着信息均值增加，知情方Reta变得越来越好”；而紧缩则意味着“随着均值增加，知情方Reta变得越来越糟”。关于信息精度，虽然在实践中不常见，文献始终将信息估计模型化为“实际值加上均值为零的随机噪声”，信息精度（方差）对应于随机噪声。

在四种具有不同复杂程度的合约中，解析和数值结果表明，对于信息倾向情形，Reta将减小a，增大b和c；对于信息精度情形，Reta偏好方差的中间值（不是越大越好）。换句话说，当Manu的估计是无偏的，自私的Reta不希望与完全知情或完全不知情的Manu交易。此外，合约的复杂性不能改变Reta对Manu信息精度的偏好。

在接下来的1.2.2节中，总结了一些基本结果，在1.2.3，1.2.4和1.2.5节中，分别对参数a，b和c的信息不对称问题进行了分析。由于在三个不对称参数的情况下得到了类似的结果，我们详细地处理参数a的情况，并概述了另外两种情况，最后给出结论，并为今后的研究指出适当的方向。