调整现金流量法也叫肯定当量法，是把不确定的现金流量调整为确定的现金流量，然后用无风险的报酬率作为折现率计算净现值。

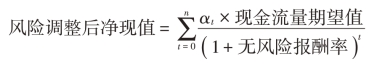
式中：αt是t年现金流量的肯定当量系数，它在0～1之间。

肯定当量系数，是指不肯定的1元现金流量期望值相当于使投资者满意的肯定的金额的系数。它可以把各年不肯定的现金流量换算为肯定的现金流量。

我们知道，肯定的1元比不肯定的1元更受欢迎。不肯定的1元，只相当于不足1元的金额。两者的差额，与现金流的不确定性程度的高低有关。肯定当量系数是指预计现金流入量中使投资者满意的无风险的份额。利用肯定当量系数，可以把不肯定的现金流量折算成肯定的现金流量，或者说去掉了现金流中有风险的部分，使之成为“安全”的现金流。去掉的部分包含了各种风险，既有特殊风险也有系统风险，既有经营风险也有财务风险，剩下的是无风险的现金流量。由于现金流中已经消除了全部风险，相应的折现率应当是无风险的报酬率。无风险的报酬率可以根据国库券的利率确定。

要确定肯定当量系数，首先应计算出现金流量的变异系数（标准离差率），然后根据变异系数与肯定当量系数间的经验数值确定肯定当量系数。

变异系数与肯定当量系数关系的经验数值：

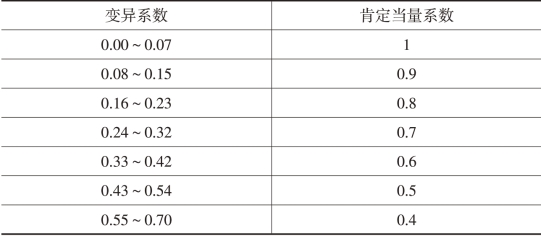
【例7-1】设当前的无风险报酬率为4%。公司有两个投资项目，有关资料如表7-1所示。

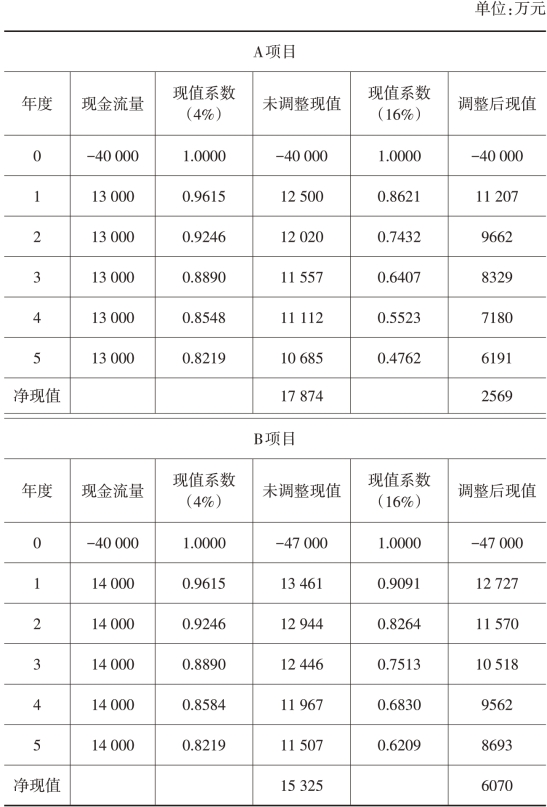
表7-1　调整现金流量法

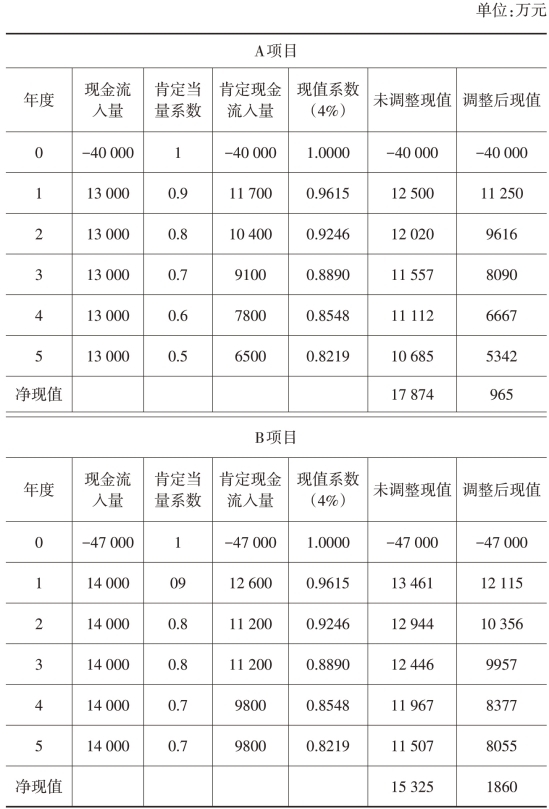
调整前A项目的净现值较大，调整后B项目的净现值较大。不进行调整，就可能导致错误的判断。

2.风险调整折现率法

风险调整折现率法是更为实际、更为常用的风险处置方法。这种方法的基本思路是对高风险的项目，采用较高的折现率计算净现值。

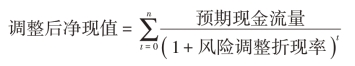(www.daowen.com)

风险调整折现率是风险项目应当满足投资人要求的报酬。项目的风险越大，要求的报酬率越高，这种方法的理论根据是资本资产定价模型。

投资者要求的收益率=无风险报酬率+β×（市场平均报酬率-无风险报酬率）

资本资产定价模型是在有效的证券市场中建立的，实物资本市场不可能像证券市场那样有效，但是基本逻辑关系是一样的。因此，上面的公式可以改为

项目要求的收益率=无风险报酬率+β×（市场平均报酬率-无风险报酬率）

【例7-2】当前的无风险报酬率为4%，市场平均报酬率为12%，A项目的β值为1.5，B项目的β值为0.75。

A项目的风险调整折现率=4%+1.5×（12%-4%）=16%

B项目的风险调整折现率=4%+0.75×（12%-4%）=10%

其他的有关数据如表7-2所示。

表7-2　风险调整折现率法

如果不进行折现率调整，两个项目净现值差不多，A项目净现值比较高；调整后，两个项目净现值有明显差别，B项目净现值要高得多。

3.两种方法的区别

调整现金流量法在理论上受到好评。该方法对时间价值和风险价值分别进行调整，先调整风险，然后对肯定现金流量用无风险报酬率进行贴现。对不同年份的现金流量，可以根据风险的差别使用不同的肯定当量系数进行调整。

风险调整折现率法在理论上受到批评，因其用单一的折现率同时完成风险调整和时间调整。这种做法意味着风险随时间推移而加大，可能与事实不符，夸大远期现金流量的风险。

实务上被普遍接受的做法是：根据项目的系统风险调整折现率，用项目的特有风险调整现金流量。