1964年，威廉·夏普（Wi11iam Sharpe）根据投资组合理论提出了资本资产定价模型（Capita1 Asset Pricing Mode1，简称CAPM）。资本资产定价模型，它第一次使人们可以量化市场的风险程度，并且能够对风险进行具体定价，具有里程碑式意义。

资本资产定价模型的研究对象，是充分组合情况下风险与必要报酬率之间的均衡关系。资本资产定价模型可用于回答如下不容回避的问题：为了补偿某一特定程度的风险，投资者应该获得多大的报酬率？在前面的讨论中，我们将风险定义为期望报酬率的不确定性；然后根据投资理论将风险区分为系统风险和非系统风险，知道了在高度分散化的资本市场里只有系统风险，并且会得到相应的回报。现在将讨论如何衡量系统风险以及如何给风险定价。

（―）系统风险的度量

既然一项资产的期望报酬率取决于它的系统风险，那么度量系统风险就成了一个关键问题。

度量一项资产系统风险的指标是β系数，用希腊字母β表示。其计算公式如下：

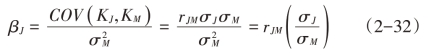
式（2-32）中：分子COV（KJ，KM）是第J种证券的报酬率与市场组合报酬率之间的协方差。它等于该证券的标准差、市场组合的标准差及两者相关系数的乘积。

从式（2-32）可以看出，一种股票的β值的大小取决于：（1）该股票与整个股票市场的相关性；（2）它自身的标准差；（3）整个市场的标准差。

β系数的计算方法有两种：

一种是使用回归直线法。根据数理统计的线性回归原理，β系数可以通过同一时期内的资产报酬率和市场组合报酬率的历史数据，使用线性回归方程预测出来。β系数就是该线性回归方程的回归系数。

【例2-15】J股票历史已获得报酬率以及市场历史已获得报酬率的有关资料如表2-6所示，计算其β值的数据准备过程如表2-7和表2-8所示。

表2-6　计算β值的数据

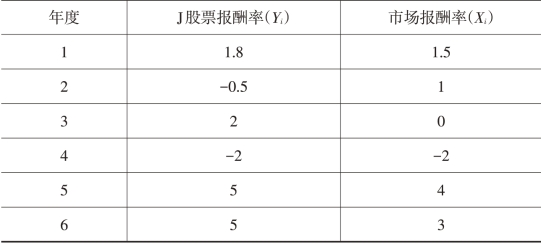
表2-7　回归直线法计算β值的数据准备

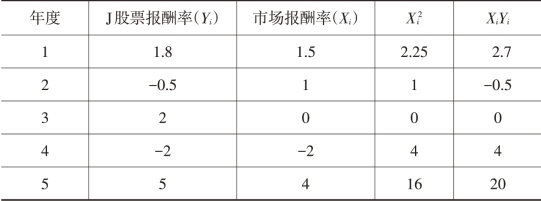
续　表

表2-8　公式法计算β值的数据准备

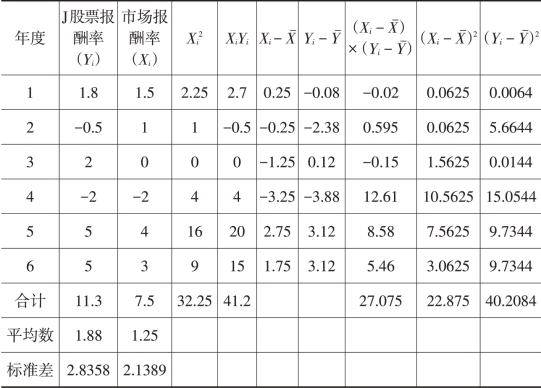
求解回归方程y=a+bx系数的计算公式如下：

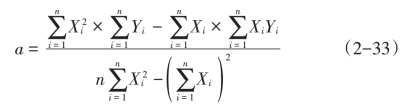
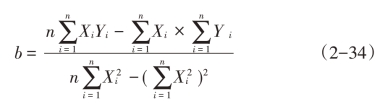
将有关数据代入式（2-33）和式（2-34）：

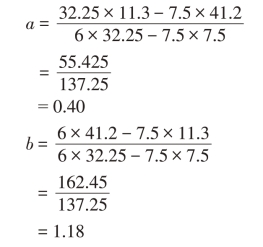
直线方程斜率b，就是该股票的β系数。

另一种方法是按照定义，根据证券与股票指数报酬率的相关系数、股票指数的标准差和股票报酬率的标准差直接计算。

相关系数的计算：

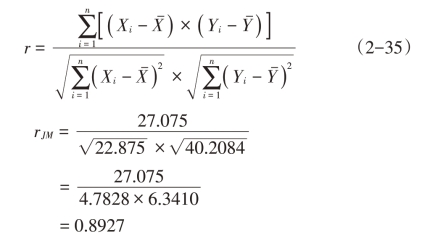
标准差的计算：

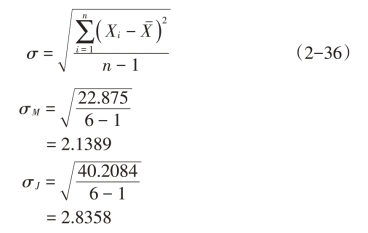
β系数的计算：

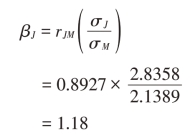
β系数的经济意义在于，它告诉我们相对于市场组合而言特定资产的系统风险是多少。例如，市场组合相对于它自己的β系数是1；如果一项资产的β=0.5，表明它的系统风险是市场组合系统风险的0.5，其报酬率的波动幅度只及一般市场波动幅度的一半；如果一项资产的β=2.0，说明这种股票的波动幅度为一般市场波动幅度的2倍。总之，某一股票β值的大小反映了该股票报酬率波动与整个市场报酬率波动之间的相关性及程度。(www.daowen.com)

（二）投资组合的β系数

投资组合的βP等于被组合各证券β值的加权平均数：

如果一个高β值股票（β＞1）被加入到一个平均风险组合（βp）中，则组合风险将会提高；反之，如果一个低β值股票（β＜1）加入到一个平均风险组合中，则组合风险将会降低。所以，一种股票的β值可以度量该股票对整个组合风险的贡献，β值可以作为这一股票风险程度的一个大致度量。

【例2-16】一个投资者拥有10万元现金进行组合投资，共投资10种股票且各占1/10即1万元。如果这10种股票的β值皆为1.18，则组合的β值为βp=1.18。该组合的风险比市场风险大，即其价格波动的范围较大，报酬率的变动也较大。现在假设完全售出其中的一种股票且以一种β=0.8的股票取而代之。此时，股票组合的β值将由1.18下降至1.142。

βp=0.9×1.18+0.1×0.8=1.142

（三）证券市场线

按照资本资产定价模型理论，单一证券的系统风险可由β系数来度量，而且其风险与收益之间的关系可由证券市场线来描述。

这个等式被称为资本资产定价模型。式（2-38）中：Ri是第i个股票的必要报酬率；Rf是无风险报酬率（通常以国库券的报酬率作为无风险报酬率）；Rm是平均股票的必要报酬率（指β=1的股票的必要报酬率，也是指包括所有股票的组合即市场组合的必要报酬率）。在均衡状态下，（Rm-Rf）是投资者为补偿承担超过无风险报酬的平均风险而要求的额外收益，即风险价格（见图2-16）。

证券市场线的主要含义如下：

（1）纵轴为必要报酬率，横轴则是以β值表示的风险。

（2）无风险证券的β=0，故Rf成为证券市场线在纵轴的截距。

（3）证券市场线的斜率[△Y/△X=(Rm-Rf)/(1-0)=12%-8%=4%]表示经济系统中风险厌恶感的程度。一般来说，投资者对风险的厌恶感越强，证券市场线的斜率越大，对风险资产所要求的风险补偿越大，风险资产的必要报酬率越高。

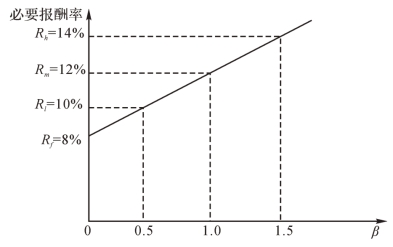
图2-16　证券市场线：β值与必要报酬率

（4）在β值分别为0.5、1和1.5的情况下，必要报酬率由最低RL=10%，到市场平均的Rm=12%，再到最高的Rh=14%。β值越大，必要报酬率越高。

从证券市场线可以看出，投资者的必要报酬率不仅取决于市场风险，而且还取决于无风险报酬率（证券市场线的截距）和市场风险补偿程度（证券市场线的斜率）。由于这些因素始终处于变动之中，所以证券市场线也不会一成不变。预计通货膨胀提高时，无风险报酬率会随之提高，进而导致证券市场线的向上平移。风险厌恶感的加强，会提高证券市场线的斜率。

需要说明的是，图2-16的证券市场线与图2-14的资本市场线是两条完全不同的直线，它们之间有着明显的区别。资本市场线描述的是由风险资产和无风险资产构成的投资组合的有效边界。其中最优投资组合由两部分组成：一部分是无风险资产，另一部分则是风险资产组合有效集上的一个风险组合。资本市场线上的M点代表的就是这一风险组合；而资本市场线上的其他点，则表示由M点与无风险资产以不同比例所构成的投资组合。其测度风险的工具是整个资产组合的标准差，此直线只适用于有效组合。

而证券市场线描述的则是在市场均衡条件下单项资产或资产组合（不论它是否已经有效地分散风险）的必要报酬率与风险之间的关系。测度风险的工具是单项资产或资产组合对于整个市场组合方差的贡献程度即β系数。

此外，需要注意的是，必要报酬率也称最低要求报酬率，是指准确反映预期未来现金流量风险的报酬率，是等风险投资的机会成本；期望报酬率则是使净现值为零的报酬率。期望报酬率和必要报酬率的关系，决定了投资者的行为。以股票投资为例，当期望报酬率大于必要报酬率时，表明投资会有超额回报，投资者应购入股票；当期望报酬率小于必要报酬率时，表明投资无法获得应有回报，投资者应卖出股票；当期望报酬率等于必要报酬率时，表明投资获得与所承担风险相应的回报，投资者投资该股票与投资其他项目相同。在完美的资本市场上，投资的期望报酬率等于必要报酬率。

（四）资本资产定价模型的假设

资本资产定价模型建立在如下基本假设之上：

（1）所有投资者均追求单期财富的期望效用最大化，并以各备选组合的期望收益和标准差为基础进行组合选择。

（2）所有投资者均可以无风险报酬率无限制地借入或贷出资金。

（3）所有投资者拥有同样预期，即对所有资产报酬的均值、方差和协方差等，投资者均有完全相同的主观估计。

（4）所有的资产均可被完全细分，拥有充分的流动性且没有交易成本。

（5）没有税金。

（6）所有投资者均为价格接受者，即任何一个投资者的买卖行为都不会对股票价格产生影响。

（7）所有资产的数量是给定的和固定不变的。

在以上假设的基础上，构建了具有奠基意义的资本资产定价模型。随后，每一个假设逐步被放开，并在新的基础上进行研究，这些研究成果都是对资本资产定价模型的突破与发展。多年来，资本资产定价模型经受住了大量经验上的考验，尤其是β概念。

自资本资产定价模型构建以来，各种理论争议和经验证明便不断涌现。尽管该模型存在许多问题，但它还是以科学的简单性、逻辑的合理性赢得了人们的支持。各种实证研究已验证了β概念的科学性及适用性。