投资组合理论认为，若干种证券组成的投资组合，其收益是这些证券收益的加权平均数，但是其风险不是这些证券风险的加权平均风险，投资组合能降低风险。

这里的“证券”是“资产”的代名词，它可以是任何产生现金流的东西，例如，一项生产性实物资产、一条生产线或者是一个企业。

（一）证券组合的期望报酬率和标准差

1.期望报酬率

两种或两种以上证券的组合，其期望报酬率可以直接表示为

式（2-27）中：rj是第j种证券的期望报酬率；Aj是第j种证券在全部投资额中的比重；m是组合中的证券种类总数。

2.标准差与相关性

证券组合的标准差并不是单个证券标准差的简单加权平均。证券组合的风险不仅取决于组合内的各证券的风险，还取决于各个证券之间的关系。

【例2-13】假设投资100万元，A方案和B方案各占50%。如果A方案和B方案标准差相等且完全负相关，即一个变量的增加值永远等于另一个变量的减少值，则组合的风险被全部抵消，如表2-3所示。如果A方案和B方案标准差相等且完全正相关，即一个变量的增加值永远等于另一个变量的增加值，则组合的风险不减少也不扩大，如表2-4所示。

表2-3　完全负相关的证券组合数据

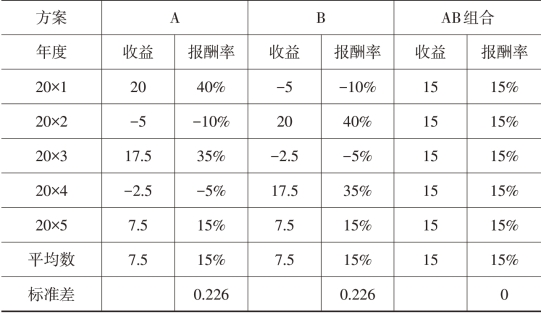
表2-4　完全正相关的证券组合数据

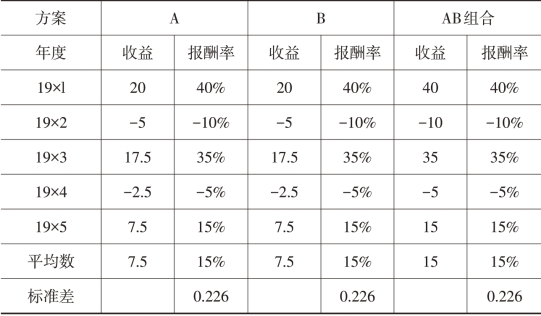
实际上，各种证券之间不可能完全正相关，也不可能完全负相关，所以不同证券的投资组合可以降低风险，但又不能完全消除风险。一般而言，证券的种类越多，风险越小。

（二）投资组合的风险计量

投资组合的风险不是各证券标准差的简单加权平均数，那么它如何计量呢？

投资组合报酬率概率分布的标准差是：

式（2-28）中：m是组合内证券种类总数；Aj是第j种证券在投资总额中的比例；Ak是第k种证券在投资总额中的比例；σjk是第j种证券与第k种证券报酬率的协方差。

式（2-28）的含义说明如下：

1.协方差的计算

两种证券报酬率的协方差，用来衡量它们之间共同变动的程度：

式（2-29）中：rjk是证券j和证券k报酬率之间的预期相关系数，σj是第j种证券的标准差，σk是第k种证券的标准差。

证券j和证券k报酬率概率分布的标准差的计算方法，前面讲述单项证券标准差时已经介绍过。

相关系数总是在-1～1间取值。当相关系数为1时，表示一种证券报酬率的增长总是与另一种证券报酬率的增长成比例，反之亦然；当相关系数为-1时，表示一种证券报酬率的增长总是与另一种证券报酬率的减少成比例，反之亦然；当相关系数为0时，表示缺乏相关性，每种证券的报酬率相对于另外的证券的报酬率独立变动。一般而言，多数证券的报酬率趋于同向变动，因此两种证券之间的相关系数多为小于1的正值。

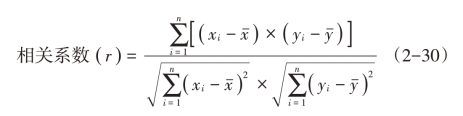
2.协方差矩阵

根号内双重的∑符号，表示对所有可能配成组合的协方差，分别乘以两种证券的投资比例，然后求其总和。

例如，当m为3时，所有可能的配对组合的协方差矩阵如下所示：

σ1，1　 σ1，2　 σ1，3

σ2，1　σ2，2　 σ2，3

σ3，1　σ3，2　σ3，3

矩阵左上角的组合（1，1）是σ1与σ1之积，即标准差的平方，称为方差，此时，j=k。从左上角到右下角，共有三种j=k的组合，在这三种情况下，影响投资组合标准差的是三种证券的方差。当j=k时，相关系数是1，并且σj×σk变为σj2。这就是说，对于矩阵对角线位置上的投资组合，其协方差就是各证券自身的方差。

组合σ1，2代表证券1和证券2报酬率的协方差，组合σ2，1代表证券2和证券1报酬率的协方差，它们的数值是相同的。这就是说需要计算两次证券1和证券2之间的协方差。对于其他不在对角线上的配对组合的协方差，我们同样计算了两次。

双重求和符号，就是把由各种可能配对组合构成的矩阵中的所有方差项和协方差项加起来。3种证券的组合，一共有9项，由3个方差项和6个协方差项（3个计算了两次的协方差项）组成。

3.协方差比方差更重要

影响证券组合的标准差不仅取决于单个证券的标准差，而且还取决于证券之间的协方差。随着证券组合中证券个数的增加，协方差项比方差项越来越重要。这一结论可以通过考察上述矩阵得到证明。例如，在两种证券的组合中，沿着对角线有2个方差项σ1，1和σ2，2，以及两项协方差项σ1，2和σ2，1。对于三种证券的组合，沿着对角线有3个方差项σ1，1、σ2，2、σ3，3以及6项协方差项。在四种证券的组合中，沿着对角线有4项方差项和12项协方差项。当组合中证券数量较多时，总方差主要取决于各证券间的协方差。例如，在含有20种证券的组合中，矩阵共有20个方差项和380个协方差项。当一个组合扩大到能够包含所有证券时，只有协方差是重要的，方差项将变得微不足道。因此，充分投资组合的风险，只受证券之间协方差的影响，而与各证券本身的方差无关。

下面举例说明两种证券组合报酬率的期望值和标准差的计算过程。

【例2-14】假设A证券的期望报酬率为10%，标准差是0.12。B证券的期望报酬率是18%，标准差是0.20。假设等比例投资于两种证券，即各占50%。

该组合的期望报酬率为

rp=10%×0.5+18%×0.5=14%

如果两种证券预期报酬率的相关系数等于1，没有任何抵消作用，在等比例投资的情况下该组合的标准差等于两种证券各自标准差的简单算术平均数，即0.16。

如果两种证券预期报酬率的相关系数是0.2，组合的标准差会小于加权平均的标准差，其标准差是：

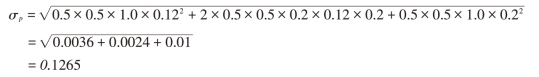
从这个计算过程可以看出：只要两种证券预期报酬率的相关系数小于1，证券组合报酬率的标准差就小于各证券报酬率标准差的加权平均数。

（三）两种证券组合的投资比例与有效集

在【例2-14】中，两种证券的投资比例是相等的。如投资比例变化了，投资组合的期望报酬率和标准差也会发生变化。对于这两种证券的其他投资比例的组合，计算结果如表2-5所示。(www.daowen.com)

表2-5　不同投资比例的组合

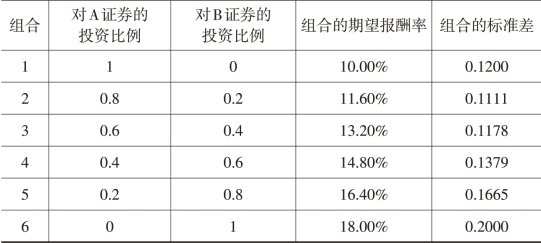
图2-11描绘出随着对两种证券投资比例的改变，期望报酬率与风险之间的关系。图中黑点与表2-5中的6种投资组合一一对应。连接这些黑点所形成的曲线称为机会集，它反映风险与收益之间的权衡关系。

图2-11有几项特征是非常重要的：

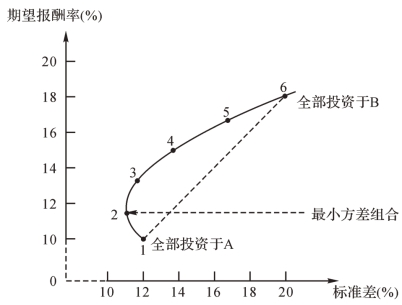
图2-11　投资于两种证券组合的机会集

（1）它揭示了分散化效应。比较曲线和以虚线绘制的直线的距离可以判断分散化效应的大小。该直线是由全部投资于A证券和全部投资于B证券所对应的两点连接而成。它是当两种证券完全正相关（无分散化效应）时的机会集曲线。曲线则代表相关系数为0.2时的机会集曲线。从曲线和直线间的距离，我们可以看出本例的风险分散效果是相当显著的。投资组合的抵消风险的效应可以通过曲线第1点至第2点的弯曲看出来。从第1点出发，拿出一部分资金投资于标准差较大的B证券会比将全部资金投资于标准差较小的A证券的组合标准差还要小。这种结果与人们的直觉相反，揭示了风险分散化的内在特征。一种证券的未预期变化往往会被另一种证券的反向未预期变化所抵消。尽管从总体上看，这两种证券是同向变化的，但抵消效应还是存在的，在图2-11中表现为机会集曲线有一段弯曲。

（2）它表达了最小方差组合。曲线最左端的第2点组合被称作最小方差组合，它在持有证券的各种组合中有最小的标准差。本例中，最小方差组合是80%的资金投资于A证券、20%的资金投资于B证券。离开此点，无论增加还是减少投资于B证券的比例，都会导致标准差的小幅上升。必须注意的是，分散化投资并不必然导致机会集曲线向点A左侧凸岀，它取决于相关系数的大小。

（3）它表达了投资的有效集合。在只有两种证券的情况下，投资者的所有投资机会只能出现在机会集曲线上，而不会出现在该曲线上方或下方。改变投资比例只会改变组合在机会集曲线上的位置。最小方差组合以下的组合（曲线第1点至第2点的部分）是无效的。没有人会持有期望报酬率比最小方差组合期望报酬率还低的投资组合，它们不但比最小方差组合风险大，而且报酬低。因此，机会集曲线第1点至第2点的弯曲部分是无效的，它们与最小方差组合相比不但标准差大（即风险大），而且报酬率也低。本例中，有效集是第2点至第6点之间的那段曲线，即从最小方差组合点到最高期望报酬率组合点的那段曲线。

（四）相关性对风险的影响

图2-11中，只示例了相关系数为0.2和1的机会集曲线，如果增加一条相关系数为0.5的机会集曲线，就成为图2-12。从图2-12中可以看到：（1）相关系数为0.5的机会集曲线与完全正相关的直线的距离缩小了，并且没有向点1左侧凸出的现象。（2）最小方差组合是100%投资于A证券。将任何比例的资金投资于B证券，所形成的投资组合的方差都会高于将全部资金投资于风险较低的A证券的方差。因此，新的有效边界就是整个机会集。（3）证券报酬率之间的相关系数越小，机会集曲线就越弯曲，风险分散化效应也就越强。证券报酬率之间的相关系数越大，风险分散化效应就越弱。完全正相关的投资组合，不具有风险分散化效应，其机会集是一条直线。

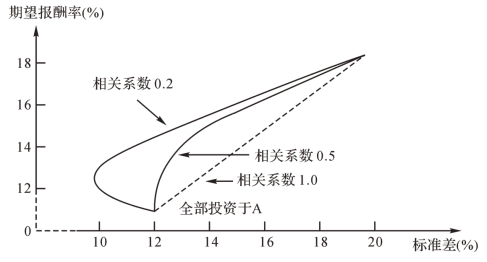
图2-12　相关系数机会集曲线

（五）多种证券组合的风险和收益

对于由两种以上证券构成的组合，以上原理同样适用。值得注意的是，多种证券组合的机会集不同于两种证券组合的机会集。两种证券的所有可能组合都落在一条曲线上，而两种以上证券的所有可能组合会落在一个平面中，如图2-13的阴影部分所示。这个机会集反映了投资者所有可能的投资组合，阴影部分中的每一点都与一种可能的投资组合相对应。随着可供投资的证券数量的增加，所有可能的投资组合数量将呈几何级数上升。

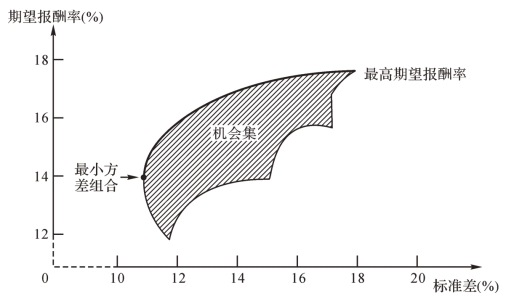
图2-13　机会集示例

最小方差组合是图2-13中最左端的点，它具有最小组合标准差。多种证券组合的机会集外缘有一段向后弯曲，这与两种证券组合中的现象类似：不同证券报酬率的波动相互抵消，产生风险分散化效应。

在图2-13中以粗线描出的部分，称为有效集或有效边界，它位于机会集的顶部，从最小方差组合点起到最高期望报酬率点止。投资者应在有效集上寻找投资组合。有效集以外的投资组合与有效边界上的组合相比，有三种情况：相同的标准差和较低的期望报酬率；相同的期望报酬率和较高的标准差；较低的期望报酬率和较高的标准差。这些投资组合都是无效的。如果你的投资组合是无效的，可以通过改变投资比例转换到有效边界上的某个组合，以达到提高期望报酬率而不增加风险，或者降低风险而不降低期望报酬率，或者得到一个既提高期望报酬率又降低风险的组合。

（六）资本市场线

如图2-14所示，从无风险资产的报酬率（Y轴的Rf）开始，做有效边界的切线，切点为M，该直线被称为资本市场线。

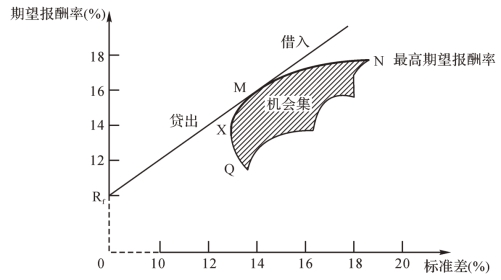
图2-14　资本市场线：最佳组合的选择

现将资本市场线的有关问题说明如下：

（1）假设存在无风险资产。投资者可以在资本市场上借到钱，将其纳入自己的投资总额，或者可以将多余的钱贷岀。无论借入还是贷出，利息都是固定的无风险资产的报酬率。Rf代表无风险资产的报酬率，它的标准差为零，即报酬率是确定的。

（2）存在无风险资产的情况下，投资人可以通过贷出资金减少自己的风险，当然同时也会降低期望报酬率。最厌恶风险的人可以全部将资金贷出，例如购买政府债券并持有至到期。偏好风险的人可以借入资金（对无风险资产的负投资），增加购买风险资产的资本，以使期望报酬率增加。

式（2-31）中：Q代表投资者投资于风险组合M的资金占自有资本总额的比例；1-Q代表投资于无风险资产的比例。

如果贷出资金，Q将小于1；如果是借入资金，Q会大于1。

总标准差=Q×风险组合的标准差

此时不用考虑无风险资产，因为无风险资产的标准差等于零。如果贷出资金，Q小于1，他承担的风险小于市场平均风险；如果借入资金，Q大于1，他承担的风险大于市场平均风险。

（3）切点M是市场均衡点，它代表唯一最有效的风险资产组合，它是所有证券以各自的总市场价值为权数的加权平均组合，我们将其定义为“市场组合”。虽然理智的投资者可能选择XMN线上的任何有效组合（它们在任何给定风险水平下收益最大），但是无风险资产的存在，使投资者可以同时持有无风险资产和市场组合（M），从而位于MRf上的某点。MRf上的组合与XMN上的组合相比，风险小而报酬率相同，或者报酬率高而风险相同，或者报酬率高且风险小。

（4）图2-14中的直线揭示出持有不同比例的无风险资产和市场组合情况下风险和期望报酬率的权衡关系。直线的截距表示无风险报酬率，它可以视为等待的报酬率。直线的斜率代表风险的市场价格，它告诉我们当标准差增长某一幅度时要求的报酬率相应增长的幅度。直线上的任何一点都可以告诉我们投资于市场组合和无风险资产的比例。在M点的左侧，你将同时持有无风险资产和风险资产组合。在M点的右侧，你将仅持有市场组合M，并且会借入资金以进一步投资于组合M。

（5）个人的效用偏好与最佳风险资产组合相独立（或称相分离）。投资者个人对风险的态度仅仅影响借入或贷出的资金量，而不影响最佳风险资产组合。其原因是当存在无风险资产并可按无风险报酬率自由借贷时，市场组合优于所有其他组合。对于不同风险偏好的投资者来说，只要能以无风险报酬率自由借贷，他们就会选择市场组合M。这就是所谓的分离定理。它也可表述为最佳风险资产组合的确定独立于投资者的风险偏好。它取决于各种可能风险组合的期望报酬率和标准差。个人的投资行为可分为两个阶段：先确定最佳风险资产组合，后考虑无风险资产和最佳风险资产组合的理想组合。只有第二阶段受投资人风险反感程度的影响。分离定理在投资管理中非常重要，它表明企业管理层在决策时不必考虑每位股东对风险的态度。证券的价格信息完全可用于确定投资者所要求的报酬率，该报酬率可指导管理层进行有关决策。

（七）系统风险和非系统风险

在投资组合的讨论中，我们知道个别资产的风险，有些可以被分散掉，有些则不能。无法分散掉的是系统风险，可以分散掉的是非系统风险。

1.系统风险

系统风险是指由那些影响所有公司的因素引起的风险。例如，战争、经济衰退、通货膨胀、高利率等非预期的变动，对许多资产都会有影响。系统风险所影响的资产非常多，影响的程度有区别。例如，各种股票处于同一经济系统之中，它们的价格变动有趋同性，多数股票的报酬率在一定程度上正相关。经济繁荣时，多数股票的价格都上涨；经济衰退时，多数股票的价格下跌。尽管涨跌的幅度各股票有区别，但是多数股票的变动方向是一致的。所以，不管投资多样化有多充分，都不可能消除全部风险，即使购买的是全部股票的市场组合。

由于系统风险是影响整个资本市场的风险，所以也称“市场风险”。由于系统风险没有有效的方法消除，所以也称“不可分散风险”。

2.非系统风险

非系统风险是指由发生于个别公司的特有事件造成的风险。例如，一家公司的工人罢工、新产品开发失败、失去重要的销售合同、诉讼失败，或者宣告发现新矿藏、取得一个重要合同等。这类事件是非预期的、随机发生的，它只影响一个或少数公司，不会对整个市场产生太大影响。这种风险可以通过多样化投资来分散，即发生于一家公司的不利事件可以被其他公司的有利事件所抵消。

由于非系统风险是个别公司或个别资产所特有的，因此也称“特殊风险”或“特有风险”。由于非系统风险可以通过投资多样化分散掉，因此也称“可分散风险”。

由于非系统风险可以通过分散化消除，因此一个充分的投资组合几乎没有非系统风险。假设投资人都是理智的，都会选择充分投资组合，非系统风险将与资本市场无关。市场不会给予它任何价格补偿。通过分散化消除的非系统风险，几乎没有任何值得市场承认的、必须花费的成本。

我们已经知道，资产的风险可以用标准差计量。这个标准差是指它的整体风险。现在我们把整体风险划分为系统风险和非系统风险，如图2-15所示。

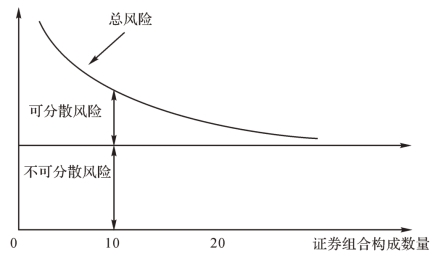
图2-15　投资组合的风险

承担风险会从市场上得到回报，回报大小仅仅取决于系统风险。这就是说，一项资产的期望报酬率高低取决于该资产的系统风险大小。

综上所述，需要掌握的主要内容是：证券组合的风险不仅与组合中每个证券的报酬率标准差有关，而且与各证券之间报酬率的协方差有关。对于一个含有两种证券的组合，投资机会集曲线描述了不同投资比例组合的风险和报酬之间的权衡关系。风险分散化效应有时使得机会集曲线向左凸出，并产生比最低风险证券标准差还低的最小方差组合。有效边界就是机会集曲线上从最小方差组合点到最高期望报酬率的那段曲线。持有多种彼此不完全正相关的证券可以降低风险。如果存在无风险证券，新的有效边界是经过无风险报酬率并和机会集相切的直线，该直线称为资本市场线，该切点被称为市场组合，其他各点为市场组合与无风险投资的有效搭配。资本市场线横坐标是标准差，纵坐标是报酬率。该直线反映两者的关系即风险价格。