风险的衡量，一般应用概率和统计方法。

（一）概率

在经济活动中，某一事件在相同的条件下可能发生也可能不发生，这类事件称为随机事件。概率就是用来表示随机事件发生可能性大小的数值。通常，把必然发生的事件的概率定为1，把不可能发生的事件的概率定为0，而一般随机事件的概率是介于0与1之间的一个数。概率越大就表示该事件发生的可能性越大。

【例2-11】ABC公司有两个投资机会，A项目是一个高科技项目，该领域竞争很激烈，如果经济发展迅速并且该项目搞得好，取得较大市场占有率，利润会很大。否则，利润很小甚至亏本。B项目是一个老产品并且是必需品，销售前景可以准确预测出来。假设未来的经济情况只有繁荣、正常、衰退三种，有关的概率分布和期望报酬率如表2-1所示。

表2-1　公司未来经济情况表

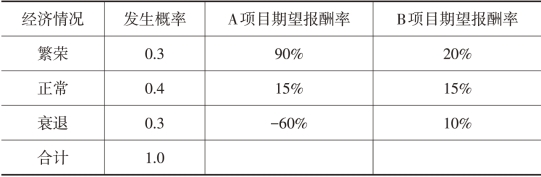
在这里，概率表示每一种经济情况出现的可能性，同时也是各种不同期望报酬率出现的可能性。例如，未来经济情况出现繁荣的可能性有0.3。假如这种情况真的出现，A项目可获得高达90%的报酬率，这也就是说，采纳A项目获利90%的可能性是0.3。当然，报酬率作为一种随机变量，受多种因素的影响。我们这里做了简化，假设其他因素都相同，只有经济情况一个因素影响报酬率。

（二）离散型分布和连续型分布

如果随机变量（如报酬率）只取有限个值，并且对应于这些值有确定的概率，则称随机变量是离散型分布。前面的【例2-11】就属于离散型分布，每一个项目都有三个值，如图2-9所示。

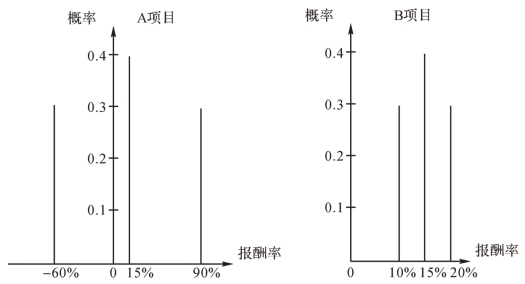
图2-9　离散型分布图

实际上出现的经济情况远不止三种，有无数可能的情况会出现。如果对每种情况都赋予一个概率，并分别测定其报酬率，则可用连续型分布描述，如图2-10所示。

图2-10　连续型分布图

从图2-10可以看到，我们给出的例子的报酬率呈正态分布，其主要特征是曲线为对称的钟形。实际上并非所有问题都按正态分布。但是，按照统计学的理论，不论总体分布是正态还是非正态，当样本很大时，其样本平均数都呈正态分布。一般来说，如果被研究的量受彼此独立的大量偶然因素的影响，并且每个因素在总的影响中只占很小部分，那么，这个总影响所引起的数量上的变化，就近似服从于正态分布。所以，正态分布在统计学上被广泛使用。

（三）预期值

随机变量的各个取值，以相应的概率为权数的加权平均数，叫做随机变量的预期值（数学期望或均值），它反映随机变量取值的平均化。

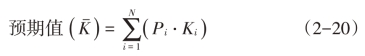
式（2-20）中：Pi——第i种结果出现的概率；

　　　　　　　Ki——第i种结果的报酬率；

　　　　　　　N——所有可能结果的数目。

据此计算：

期望报酬率（A）=0.3×90%+0.4×15%+0.3×（-60%）=15%

期望报酬率（B）=0.3×20%+0.4×15%+0.3×10%=15%(www.daowen.com)

两者的期望报酬率相同，但其概率分布不同（见图2-10）。A项目的报酬率的分散程度大，变动范围在-60%～90%之间；B项目的报酬率的分散程度小，变动范围在10%～20%之间。这说明两个项目的报酬率相同，但风险不同。为了定量地衡量风险大小，还要使用统计学中衡量概率分布离散程度的指标。

（四）离散程度

表示随机变量离散程度的量数，最常用的是方差和标准差。

方差是用来表示随机变量与期望值之间离散程度的一个量，它是离差平方的平均数。

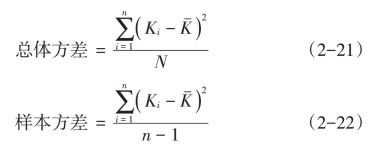
标准差是方差的平方根：

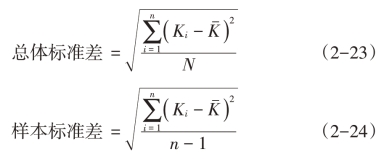
总体，是指我们准备加以测量的一个满足指定条件的元素或个体的集合，也称母体。在实际工作中，为了了解研究对象的某些数学特性，往往只能从总体中抽出部分个体作为资料，用数理统计的方法加以分析。这种从总体中抽取部分个体的过程称为抽样，所抽的部分称为样本。通过对样本的测量，可以推测整体的特征。

为什么样本标准差的n个离差平方不除以n，而要除以（n-1）呢？

n表示样本容量（个数），（n-1）称为自由度。自由度反映分布或差异信息的个数。例如，当n=1时，即Ki只有一个数值时，（K1-=0，数据和均值没有差异，即表示差异的信息个数为1-1=0；当n=2时是K1和K2的中值，则的绝对值相等，只是符号相反。它们只提供一个信息，即两个数据与中值相差这就是说差异的个数为2-1=1。当n=3时，也是如此。例如，K分别为1、2、6时，均值为3，误差分别为-2、-1和3。实际上，我们得到的误差信息只有两个。因为比均值小的数据的误差绝对值与比均值大的数据的误差绝对值是相等的。我们知道了两个误差信息，就等于知道了第三个误差信息。例如，一个数据比均值小2，一个数据比均值小1，则另一个数据必定比均值大3。当n为4或更多时，数据与均值的误差信息总会比样本容量少一个。因此，要用（n-1）作为标准差的分母。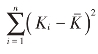只有（n-1）个对我们有用的信息，所以用（n-1）作为分母才是真正的平均。

由于在项目投资管理实务中使用的样本量都很大，区分总体标准差和样本标准差没有什么实际意义。如果样本量比较小，则应当加以区分。

在已经知道每个变量值出现概率的情况下，标准差可以按下式计算：

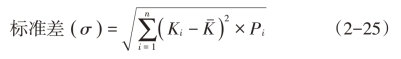
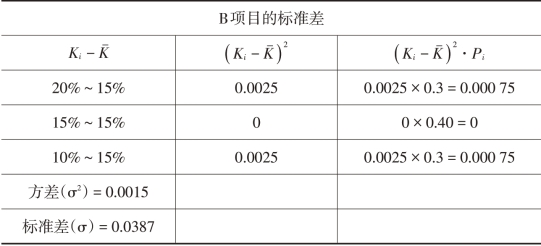
A项目的标准差是0.5809，B项目的标准差是0.0387（计算过程如表2-2所示），由于它们的期望报酬率相同，因此可以认为A项目的风险比B项目大。

表2-2　项目标准差计算表

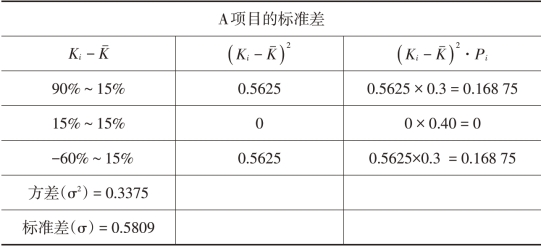
续　表

标准差是以均值为中心计算出来的，因而有时直接比较标准差是不准确的，需要剔除均值大小的影响。为了解决这个问题，引入了变异系数（离散系数）的概念。变异系数是标准差与均值的比，它是从相对角度观察的差异和离散程度，在比较相关事物的差异程度时较之直接比较标准差要好些。

【例2-12】A证券的期望报酬率为10%，标准差是0.12；B证券的期望报酬率为18%，标准差是0.20。

变异系数（A）=0.12/10%=1.20

变异系数（B）=0.20/18%=1.11

直接从标准差看，B证券的离散程度较大，能说B证券的风险比A证券大吗？不能轻易下这个结论，因为B证券的平均报酬率较大。如果以各自的平均报酬率为基础观察，A证券的标准差是其均值的1.20倍，而B证券的标准差只是其均值的1.11倍，B证券的相对风险较小。这就是说，A证券的绝对风险较小，但相对风险较大，B证券与此正相反。