为了计算货币时间价值,需要引入“终值”和“现值”这两个概念,以表示不同时点的货币价值。终值是指现在的一定量货币在将来某一时点的价值,包括本金和时间价值,即“本利和”;现值是指将来某一时点的一定量货币相对于现在的价值,即未来值扣除时间价值后所剩的“本金”。同时,为了方便起见,假定货币的流入或流出都是在某一时期(通常为1年)的起始或终了时进行。
(一)单利的计算
1.单利终值
单利终值是指现在一定量货币在若干期后按单利法计算利息的本利和。单利法是指只有本金计算利息,每期产生的利息都不能与本金一起计算下一期的利息,即利息不再生息。如我国银行存款就是按单利法计算利息的。
单利终值的计算公式为
![]()
式(2-1)中:P为现值(或本金);i为利率(一般指年利率);n为计息期数;F为n期后的终值。
单利终值计算公式的推导过程如下:
每期利息为P·i
n期后的总利息为P·i·n
由此可以得出n期后的本利和为P+P·i·n=P·(1+i·n)
【例2-1】某企业将10万元存入银行,假设年利率为5%,则5年后的单利终值为
F=10×(1+5%×5)=12.5(万元)
2.单利现值
单利现值是指以后某一时间收到或付出的货币按单利法倒求的现在价值(即本金)。由终值求现值称为折现,折现的利率称为折现率。
单利现值的计算公式可从单利终值的计算公式推导得出:

式(2-2)中:P为现值;F为n期后收到或付出的货币量(终值);i为折现率;n为折现期数。
【例2-2】某企业希望5年后能从银行提取10万元,在年利率为5%的情况下,现在就应该存入银行的本金为
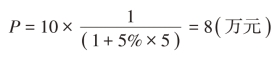
(二)复利的计算
复利是指每期产生的利息并入本金一起参与计算下一期利息的计息方法。按照这种方法,要将所生利息加入本金再计利息,逐期滚算,俗称“利滚利”。
1.复利终值
复利终值是指现在一定量货币在若干期后按复利法计算利息的本利和。复利终值的计算公式为
![]()
式(2-3)中:F为n期后的终值;P为本金;i为利率;n为计息期数。
复利终值计算公式的推导过程如下:
第1期后的终值为P+P·i=P·(1+i)
第2期后的终值为![]()
……
第n期后的终值为P·(1+i)n
【例2-3】某企业现在将10万元存入银行,若年利率为5%,按复利法计息,则5年后的复利终值为
F=10×(1+5%)5=12.76(万元)
复利终值计算公式中的(1+i)n称为复利终值系数,或称为1元的复利终值,用(F/P,i,n)表示。因此,复利终值的计算公式又可表示为
![]()
为了简化和加速计算,事先可以编制复利终值系数表(见本书附表一),该表的第一行是利率i,第一列是计息期n,相应的(1+i)n值在其纵横相交处。通过查复利终值系数表的方法得到相应的复利终值系数。例如,(F/P,5%,5)表示利率为5%的5期复利终值的系数。
如【例2-3】查表计算如下:
![]()
2.复利现值
复利现值是指以后某一时间收到或付出的货币按复利贴得的现在价值(即本金)。复利现值的计算公式为
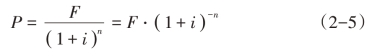
式(2-5)中:P为现值;F为n期后收到或付出的货币量(终值);i为折现率;n为折现期数。
复利现值计算公式中的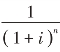 称为复利现值系数,或称为1元的复利现值,用(P/F,i,n)表示。因此,复利现值的计算公式又可表示为
称为复利现值系数,或称为1元的复利现值,用(P/F,i,n)表示。因此,复利现值的计算公式又可表示为
![]()
例如,(P/F,10%,5)表示利率为10%的5期复利现值系数。为了便于计算,事先可编制复利现值系数表(见本书附表二)。该表的使用方法与复利终值系数表的使用方法相同。
【例2-4】某企业希望5年后能从银行提取10万元,在年利率为5%的情况下,按年复利计息,则现在应该存入银行的本金为
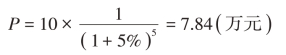
或查复利现值系数表计算如下:
P=10×(P/F,10%,5)=10×0.784=7.84(万元)
(三)年金的计算
年金是指在一定时期内,每期收到或付出的等额款项。年金的“年”是指收到或付出款项的期次,是一种通俗的说法,并非一定是一年,也可以是一个月或者一个季度。年金在日常生活中经常能够遇到,如企业采用平均年限法计算的折旧额、企业每月为职工支付的养老保险金、各种租金、退休职工的养老金等都以年金的形式出现。根据收款或付款在时间、方式上的不同,年金可以分为普通年金、预付年金、延期年金和永续年金等四种形式。
1.普通年金终值和现值的计算
普通年金是指在一定时期内,每期期末有等额的收付款项的年金。如收取债券利息、支付借款利息、获取投资净收益等都是在期末发生的,因此,普通年金又称为后付年金。
(1)普通年金终值,是指一定期间内每期期末等额的系列收付款项的复利终值之和。如零存整取的本利和。
假设,每期等额收款或付款额为A,年金期数为n,利率为i,年金终值为F。普通年金终值的计算如图2-1所示。
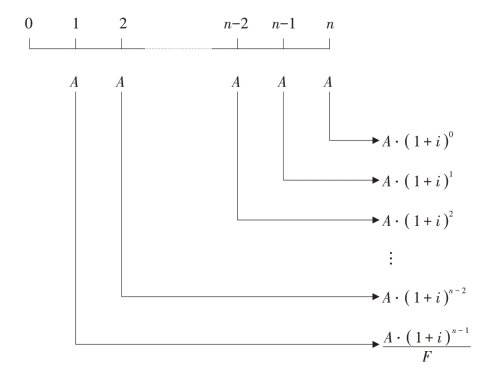
图2-1 普通年金终值的计算过程
由图2-1可知,普通年金终值的计算公式为
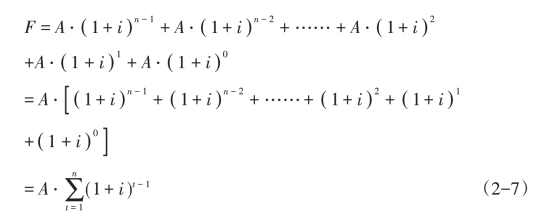
式(2-7)中的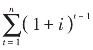 称为年金终值系数,用(F/A,i,n)表示。因此,普通年金终值的计算公式又可表示为
称为年金终值系数,用(F/A,i,n)表示。因此,普通年金终值的计算公式又可表示为
![]()
为了简化计算,也可事先编制年金终值系数表(见本书附表三),以供查找相应的年金终值系数。年金终值系数也可以按以下公式计算:
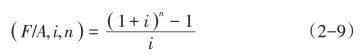
该公式的推导过程如下:
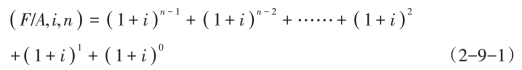
将式(2-9-1)两边同乘(1+i),得:
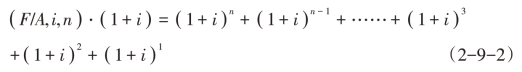
两式相减,得:
(F/A,i,n)·(1+i)-(F/A,i,n)=(1+i)n-1
(F/A,i,n)·i=(1+i)n-1
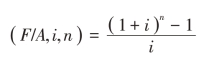
【例2-5】某企业每年年末存入银行10万元,若年利率为5%,则第5年年末的年金终值为
F=10×(F/A,i,n)=10×5.525=55.25(万元)
(2)普通年金现值,是指一定期间内每期期末等额的系列收付款项的复利现值之和。
普通年金现值用P表示。普通年金现值的计算如图2-2所示。
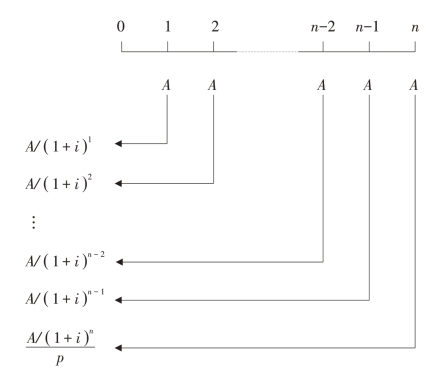
图2-2 普通年金现值的计算过程
由图2-2可知,普通年金现值的计算公式为(https://www.daowen.com)
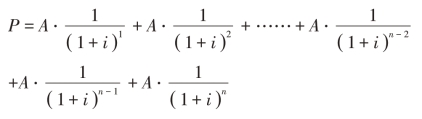

式(2-10)中的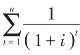 称为年金现值系数,或称为年金折现系数,用(P/A,i,n)表示。因此,普通年金现值的计算公式又可表示为
称为年金现值系数,或称为年金折现系数,用(P/A,i,n)表示。因此,普通年金现值的计算公式又可表示为
![]()
为了简化计算,也可事先编制年金现值系数表(见本书附表四),以供查找相应的年金现值系数。年金现值系数也可以按以下公式计算:
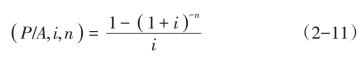
该公式的推导过程如下:
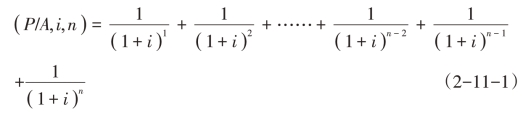
将式(2-11-1)两边同乘(1+i),得:
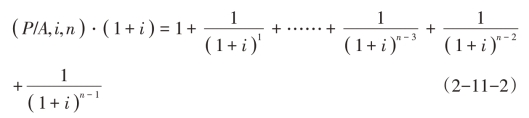
两式相减,得:
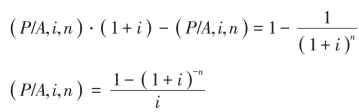
【例2-6】某企业希望连续5年的每年年末都能从银行提取10万元,若年利率为5%,则现在就应该存入银行的本金为
P=10×(P/A,5%,5)=10×4.329=43.29(万元)
2.预付年金终值和现值的计算
预付年金是指在一定时期内,每期期初有等额的收付款项的年金。预付年金与后付年金(普通年金)的区别仅仅在于收付款项的时间不同。由于普通年金是最普遍、最常用的,因此年金终值系数表和年金现值系数表都是按普通年金编制的。可以在普通年金的终值和现值计算公式的基础上,通过适当的调整,利用普通年金系数表来计算预付年金的终值和现值。
(1)预付年金终值,是指一定期间内每期期初等额的系列收付款项的复利终值之和。
n期预付年金终值和n期普通年金终值之间的关系如图2-3所示。
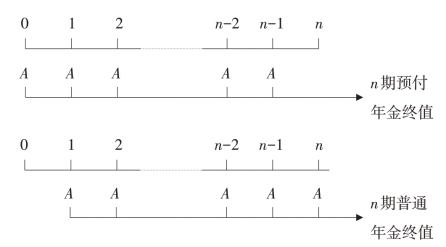
图2-3 n期预付年金终值和n期普通年金终值的关系
从图2-3中可以看出,n期预付年金终值和n期普通年金终值的收付款项的期数相同,但因收付款项的时间不同,n期预付年金的每期款项均比n期普通年金的每期款项多计算一次利息,因此,只要将n期普通年金终值乘上(1+i),便可求得n期预付年金的终值。预付年金的终值用F表示,则其计算公式为
![]()
此外,还可以根据n期预付年金终值和n+1期普通年金终值之间的关系推导出另一计算公式。n期预付年金终值和n+1期普通年金终值之间的关系如图2-4所示。

图2-4 n期预付年金终值和n+1期普通年金终值的关系
从图2-4中可以看出,n期预付年金终值和n+1期普通年金终值的计息期数相同,但收付款项的期数不同,n+1期普通年金比n期预付年金多了一期不用计息的款项,因此,只要将n+1期普通年金的终值减去这一期不用计息的款项A,便可求得n期预付年金的终值。其计算公式为
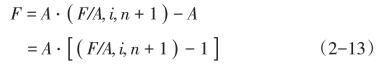
如果把式(2-13)中的[(F/A,i,n+1)-1]称为预付年金终值系数,则它同普通年金终值系数相比,是“期数加1、系数减1”,可利用普通年金终值系数表查得(n+1)期的值,再减去1而得到。
【例2-7】某企业每年年初都存入银行10万元,若年利率为5%,则第5年年末能取得的本利和为
F=10×(F/A,5%,5)×(1+5%)=10×5.525×1.05
=58.01(万元)
或F=10×[(F/A,5%,6)-1]=10×(6.801-1)=58.01(万元)
(2)预付年金现值,是指一定期间内每期期初等额的系列收付款项的复利现值之和。
n期预付年金现值与n期普通年金现值之间的关系如图2-5所示。
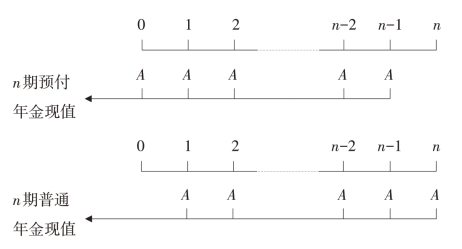
图2-5 n期预付年金现值与n期普通年金现值的关系
从图2-5中可以看出,n期预付年金现值和n期普通年金现值的收付款项的期数相同,但收付款项的时间不同,结果是n期预付年金的每期款项均比n期普通年金的每期款项少折现一期,因此,n期普通年金现值除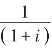 ,即乘上(1+i),便可得到n期预付年金的现值。预付年金现值用P表示,则其计算公式为
,即乘上(1+i),便可得到n期预付年金的现值。预付年金现值用P表示,则其计算公式为
![]()
此外,还可以根据n期预付年金现值和n-1期普通年金现值之间的关系推导出另一计算公式。n期预付年金现值和n-1期普通年金现值之间的关系如图2-6所示。
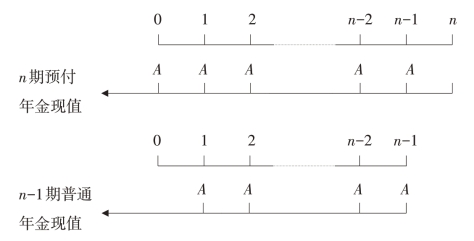
图2-6 n期预付年金现值和n-1期普通年金现值的关系
从图2-6中可以看出,n期预付年金现值和n-1期普通年金现值的折现期数相同,但收付款项的期数不同,结果是n期预付年金比n-1期普通年金多一期不用折现的款项,因此,只要将n-1期普通年金的现值加这一期不用折现的款项A,便可求得n期预付年金的现值。其计算公式为
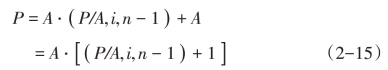
如果把式(2-15)中的(P/A,i,n-1)称为预付年金现值系数,则它同普通年金现值系数相比,是“期数减1、系数加1”,可利用普通年金现值系数表查得(n-1)期的值,再加上1而得到。
【例2-8】某企业希望连续5年的每年初都能从银行提取10万元,若年利率为5%,则现在就应该存入银行的本金为
P=10×(P/A,5%,5)×(1+5%)=10×4.329×1.05
=45.45(万元)
或P=10×[(P/A,5%,4)+1]=10×(3.545+1)=45.45(万元)
3.延期年金终值和现值的计算
延期年金是指在开始若干期没有收付款项,以后每期期末有等额收付款项的年金。
(1)延期年金终值,是指若干期后每期期末等额的系列收付款项的复利终值之和。
假设,前m期没有收付款项,后n期有等额的收付款项。则延期年金终值的计算可用图2-7说明。
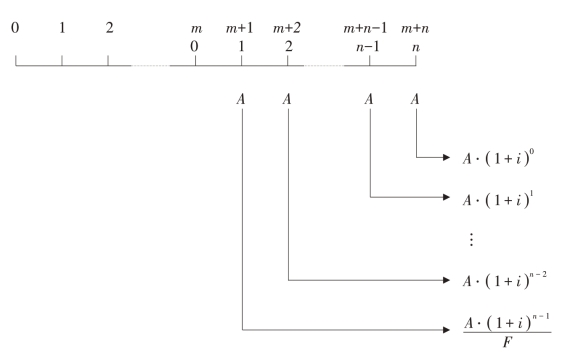
图2-7 延期年金终值的计算过程
由图2-7可知,延期年金终值大小与前m期无关,只同后n期有关。因此,求延期年金终值只要考虑实际发生收付款项的后n期年金,其计算方法与普通年金终值的计算方法相同。
(2)延期年金现值,是指若干期后每期期末等额的系列收付款项的复利现值之和。
延期年金的现值用P表示。延期m期的延期年金现值的计算如图2-8所示。
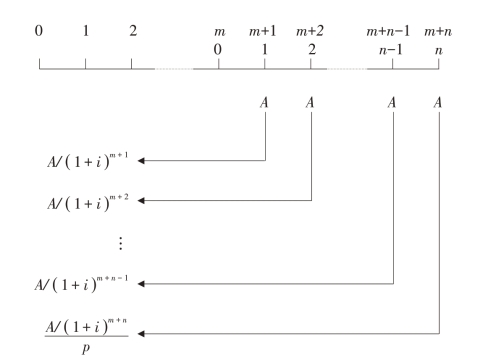
图2-8 延期年金现值的计算过程
由图2-8可知,延期年金现值等于m+n期普通年金现值减去实际没有发生收付款项的前m期普通年金现值后的差值。其计算公式为
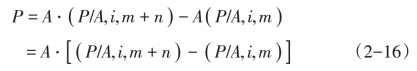
延期年金现值还可以用另一种方法计算。先求出延期年金在后n期的期初(即前m期的期末)的普通年金现值,因为前m期没有收付款项,该值就可看作前m期的复利终值,再将它折现至前m期的第一期期初,求得的复利现值即为延期年金的现值。其计算公式为
![]()
【例2-9】某企业从银行贷入一笔款项,贷款年利率为5%,银行规定前4年不用还本付息,但从第5年开始至第10年结束,每年年末须偿还本息10万元,则该款项的现值应该为
P=10×[(P/A,5%,10)-(P/A,5%,4)]
=10×(7.721-3.545)=41.76(万元)
或P=10×(P/A,5%,6)×(P/F,5%,4)
=10×5.075×0.823=41.77(万元)
4.永续年金现值的计算
永续年金是指无限期地连续收付款项的年金。如优先股的股利,应该无限期地按时等额发放,这就是一种永续年金。
永续年金由于没有终止的时间,因此没有必要计算其终值。永续年金的现值就是期数为无限的普通年金现值,其计算公式可以从普通年金现值的计算公式推导得出。
普通年金现值的计算公式为
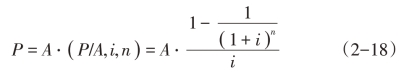
当n→∞时
则,永续年金现值的计算公式为

【例2-10】某慈善组织决定一次性存入银行一笔基金,以便以后能无限期地于每年年末提取利息10万元,用于年度的慈善活动开支。若存款年利率为5%,则该慈善组织现在应该存入银行的款项为
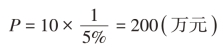
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








