在多指标评价（或决策）问题中，首先必须确定各指标的权重，指标权重的确定有主观法和客观法两大类。主观法是由评估者对各指标的主观重视程度而赋权的一类方法，主要有专家调查法（Delphi）、循环评分法、二项系数法、层次分析法（AHP）等；客观法是根据指标自身的作用和影响确定权数的方法，主要有嫡值法及主成分分析、因子分析、聚类分析、判别分析等多元分析方法。上述方法在进行综合评价分析中各有优缺点，主观赋权法客观性较差，而客观赋权法确定的权数有时与指标的实际重要程度相悖，因而，需要根据评价指标性质和评价目的进行选择配合使用。考虑到农业系统的多目标性、非线性、高阶性特点，我们在结合专家调查的基础上采用层次分析法（即群组判断方法）确定农业可持续发展指标体系中的指标权重，以克服主观赋权法的缺陷，确保指标权重的客观性。

AHP确定指标权重的一般步骤与方法。数学工具在评估中起着重要的作用，在复杂的决策与评估问题面前，人们往往利用数学模型对实际问题进行抽象和简化，进而对实际问题进行系统分析。但是，在评估或决策中，人们无法忽视或回避评估者和决策者的选择与判断所起的决定作用，因为其中总有大量因素无法直接给出定量表示。正是在这种背景下，美国著名运筹学家、匹兹堡大学教授萨蒂（T.L.Saaty）在科学研究人的选择、判断与决策的思维规律的基础上，于20世纪70年代提出了层次分析法（Analytic Hierarchy Process，简称AHP），其具体计算步骤为：

1.建构指标体系的递阶层次结构。按照评价指标体系的基本关系构建递阶层，指标体系的每层中各元素支配下一层中的相应元素，从而形成一个总目标层和若干个子准则层组成的递进的“金字塔”型层次结构。

2.建立两两判断矩阵。在确定的递阶层次结构中，每一个元素和该元素支配的下一层元素构成一个子区域，对于子区域内的各元素采用专家咨询法来构建若干个判断矩阵。

设总目标层元素A与下层元素b1，bl，…，bn有联系，则判断矩阵如下：

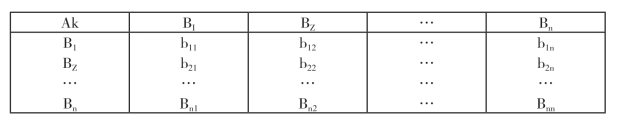
其中：bij表示对于A而言，其下一层元素Bi对Bj相对重要性的数值表现。通常运用1—9比率标度法（其含义见表9-2）将相对重要性的逻辑判断数量化，即判断矩阵的值根据专家的判断结果综合给出。

表9-2　判断矩阵1—9标度及其含义

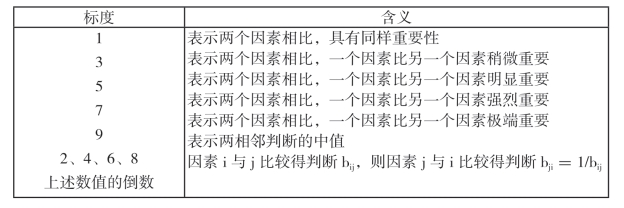
3.进行层次因素单排序值的计算。用方根法计算各指标的权值wt。

4.进行一致性检验：

首先，计算一致性指标CI＝（λmax一n）/（n一1）。(www.daowen.com)

其次，根据判断矩阵的阶数n，查找相应的平均随机一致性指标RI。对于1-15阶矩阵，RI，如下表所示：

表9-3　平均随机一致性指标

这里，对于1、2阶判断矩阵，RI只是形式上的，因为1、2阶判断矩阵总具有完全的一致性。

最后，计算一致性比率CR＝（CI）/（RI）

对于判断矩阵大于2阶时，CI与RI的比称为判断矩阵的一致性比率。当CR不满足小于0.1时，就需要调整判断矩阵直至具有满意的一致性。

5.建立B层各元素与其下层元素之间的两两判断矩阵，并完成3、4步骤的计算（如果B层下面的元素C还有下层元素，则按照上述方法继续计算）。

6.层次总排序，计算各层指标的组合权重。计算指标层所有元素对于最高层（总目标）相对重要性的排序权重，即在形成所在子系统的各自相对权重的基础上，将最后一层元素的权数依次乘以上一层受控元素的相对权数，从而形成各元素对于总目标的绝对权重。

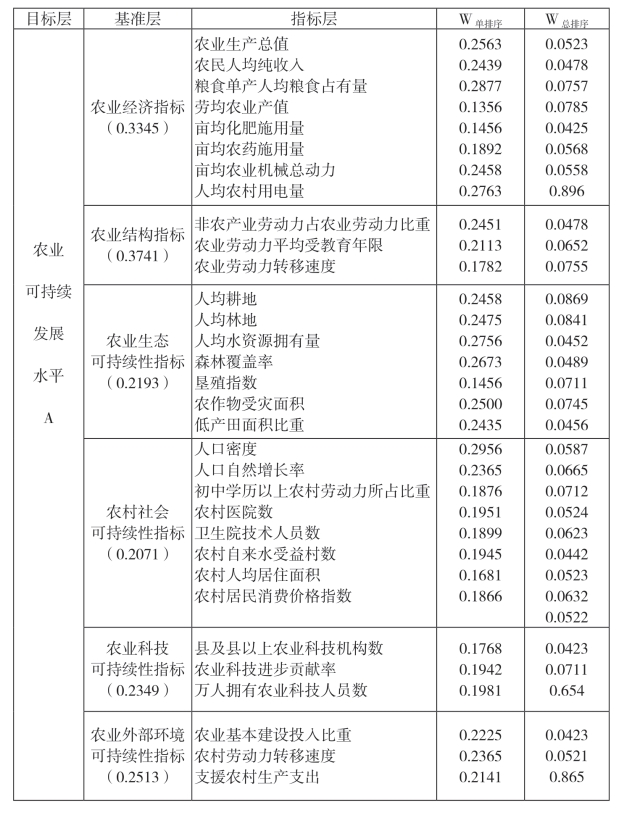
根据以上步骤，我们计算出湖南农业可持续发展指标体系的权重如表9-4：

表9-4　修正后的湖南农业可持续发展评估指标体系及其权重