1.甲医院的重建项目

为了更好地为乙县的民众服务，甲医院决定重新选址，从丙搬到丁。丁是一个大型的社区，目前还没有基本的医疗设施。搬到丁意味着需要建立一个新的医院，并开张经营。在团队成员的帮助下，项目经理已经完成了工作分解结构，整个项目由11个主要活动组成，并且确定了每一项活动的紧前活动，如表16-1所示。

表16-1 甲医院重建项目的活动

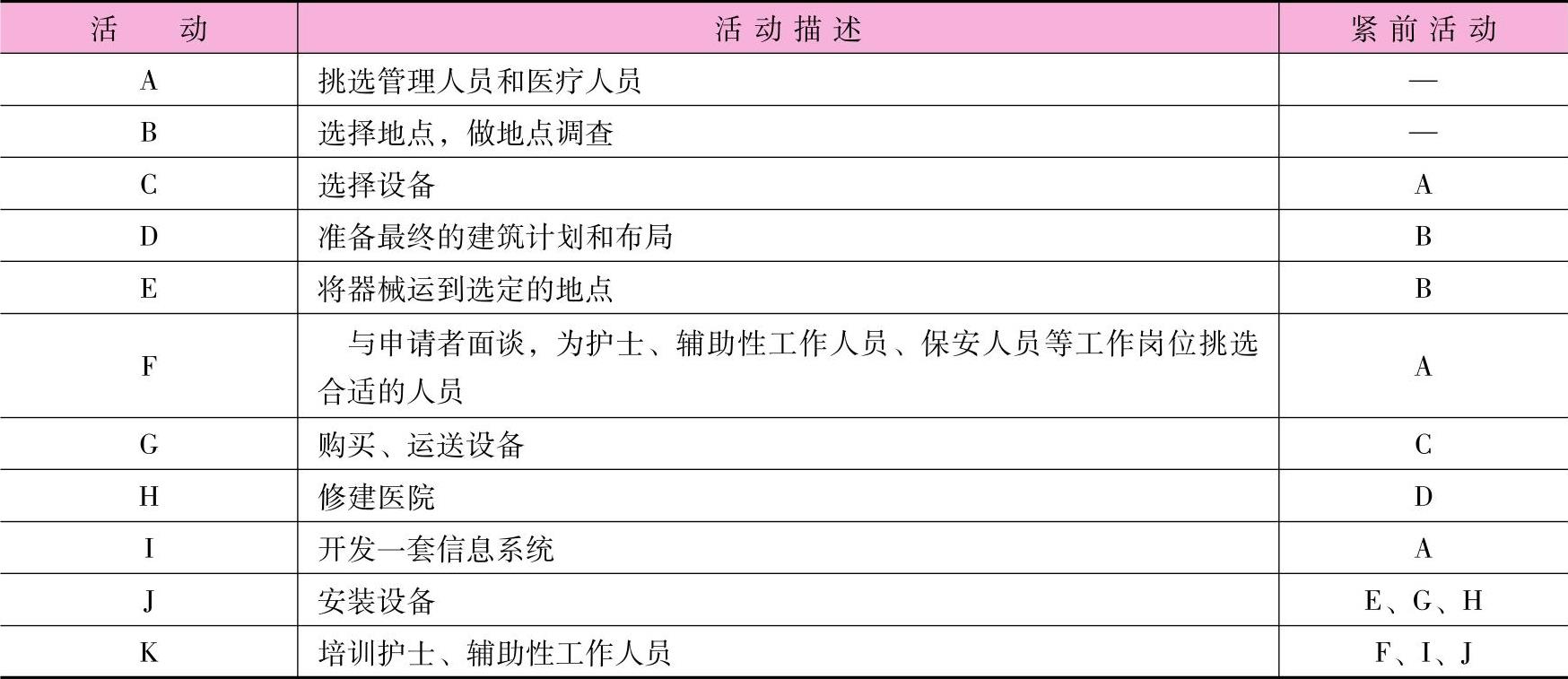
根据这11项活动及其先后关系画出节点图（图16-9），用圆圈描述活动，用箭头表示需要完成的活动，数字代表每一项活动估计用的是多少周。活动A和B是从起点发散出来的，因为其没有紧前活动。活动K与终点节点连接，因为其没有紧后活动，起点和终点并不真正代表活动，它们仅仅是在节点图中表示开始与结束地点而已。

完工时间最长的路径称为关键路径，在这条路径上若发生问题，将影响到整个工程项目的进度。在此项目中，可以通过下述的网络计划图时间计算方法确定关键路径为B→D→H→J→K，即图中为了突出而采用双箭线连接表示的活动路径，并确定完工时间为69周。显然，关键路径上的几项项目活动是项目经理最应该注意的地方。

2.网络计划图的时间参数

网络计划图的计算中需要涉及以下主要时间参数：

（1）活动持续时间D（Duration）。它是指对一项活动规定的从开始到完成的时间。在双代号网络图中，活动i-j的持续时间记为D_i-j，在单代号网络图中，活动i的持续时间记为D_i。

（2）工期T（Project Duration）。它泛指完成任务所需的时间。

（3）节点最早时间ET（Earliest Time）。它是指该节点后各活动的最早开始时间，节点i的最早时间记为ET_i。

（4）节点最迟时间LT（Latest Time）。它是指该节点前各活动的最迟完成时间，节点j的最迟时间记为LT_j。

（5）活动最早开始时间ES（Earliest Start Time）。它是指各紧前活动全部完成后，本活动有可能开始的最早时间。活动i-j的最早完成时间记为ES。显然，ES=ET_i。

（6）活动最早完成时间EF（Earliest Finish Time）。它是指各紧前活动全部完成后，本活动有可能完成的最早时间。活动i-j的最早完成时间记为EF。显然，EF=ES+D。

（7）活动最迟完成时间LF（Latest Finish Time）。它是指不影响整个项目按期完工的条件下，本活动最迟必须完成的时间。活动i-j的最迟完成时间记为LF。显然，LF=LT_j。

图16-9 甲医院重建项目节点图（单位：周）

（8）活动最迟开始时间LS（Latest Start Time）。它是指不影响整个项目按期完工的条件下，本活动最迟必须开始的时间。活动i-j的最迟开始时间记为LS。显然，ES=LF-D。

（9）活动总时差TF（Total Float）。它是指在不影响整个项目完成总工期的前提下，本活动所具有的机动时间。

（10）活动自由时差FF（Free Float）。它是指不影响紧后活动最早开始时间的前提下，本活动所具有的机动时间。

为了方便对网络计划图的各种时间参数的计算过程，可以采用图16-10所示格式来对所有的项目活动进行时间参数的计算。

3.关键路径法的计算步骤

网络计划图各时间参数的计算及确定关键路径的步骤如下：

（1）通过正向计算法获得各项目活动的最早时间。正向计算即按照从网络计划图的始端向终端的方向对节点活动进行逐个计算。根据逻辑关系，首先计算活动的最早开始时间ES，当一个活动有多个紧前活动时，该活动的ES=max{紧前活动的EF}。然后，计算最早完成时间EF，该活动的EF=该活动的ES+活动持续时间D。

（2）根据终点活动的完成时间，确定项目网络的计划工期T。

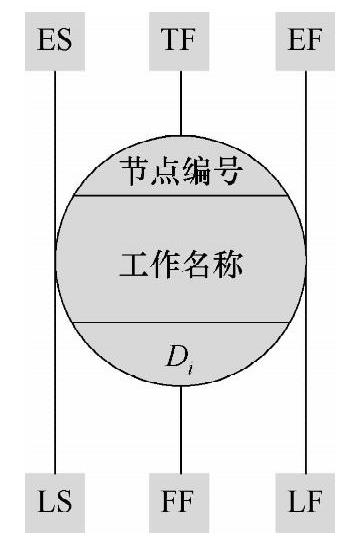
图16-10 项目活动的时间参数

（3）通过反向计算法获得各项目活动的最迟时间。反向计算即按照从网络计划图的终端向始端的方向对节点活动进行逐个计算。首先计算活动的最迟完成时间LF，当一个活动有多个紧后活动存在时，该活动的LF=min{紧后活动的LS}。然后，计算最迟开始时间LS，该活动的LS=该活动的LF-活动持续时间D。

（4）计算各项活动的总时差TF，活动总时差TF=LS-ES=LF-EF。

（5）计算各项活动的自由时差FF。当有多个紧后活动存在时，活动的自由时差FF=min{紧前活动的ES}-该活动的EF。

（6）由松弛时间为零的活动确定该项目的关键路径。关于活动松弛时间的信息具有很大的作用，因为它特别指出哪些活动应该受到重视。就此而言，活动松弛时间就是制定项目进度计划时，在整个项目不延误的前提下，下一项活动可以允许推迟的时间。关键路径上的活动松弛时间为零。当一项活动估计持续的时间太多，或者由于资源方面的考虑，该活动预计开始的时间不得不拖后时，该活动的松弛时间就会缩短。有时候项目经理可以人为地调控松弛时间，以克服进度计划中的一些问题。松弛时间的信息可以帮助项目团队作出重新分配资源方面的决策。如果在一个项目中资源可以用于不同的活动的话，那么可以把资源从那些具有松弛时间的活动中转移出来，配置到那些落后于进度计划的活动之中，直到用完活动的松弛时间为止。

4.计算示例

项目Ace的各项活动之间的关系以及其活动时间如表16-2所示，利用网络计划图计算项目工期并确定项目的关键路径。

表16-2 Ace的项目活动的依赖关系和作业时间

（1）计算最早开始时间与最早完成时间。活动A、B没有紧前活动，这两项活动的最早开始时间均为零，它们的最早完成时间为：

EF_A=0+2周=2周

EF_B=0+4周=4周(www.daowen.com)

活动C、D、E的最早开始时间为：

ES_C=2周

ES_D=max{EF_A，EF_B}=4周

ES_E=4周

进一步则得：

EF_C=2周+10周=12周

EF_D=4周+4周=8周

EF_E=4周+6周=10周

同理可知：

ES_G=max{EF_C，EF_D}=12周

ES_H=max{EF_D，EF_E}=10周

EF_G=12周+3周=15周

EF_H=10周+4周=14周

ES_I=max{EF_G，EF_H}=15周

EF_I=15周+2周=17周

由于活动I是关键路径上最后一个活动，因此项目的最早完成时间（即项目工期）为17周。

（2）计算最迟开始时间与最迟完成时间。按照前一步骤计算出的工期，将终点活动I的最迟完成时间设定为17周（也就是活动I的最早完成时间）。因此，活动I的最迟开始时间为：

LS_I=LF_I-2周=15周

如果活动I要在不迟于15周开始，该活动的所有紧前活动都必须不迟于这一时间开工，因此：

LF_G=15周

LF_H=15周

活动G、H的最迟开始时间为：

LS_G=LF_G-3周=12周

LS_H=LF_H-4周=11周

LF_C=12周

LF_D=min{LS_G、LS_H}=11周

LF_E=11周

LS_C=LF_C-10周=2周

LS_D=LF_D-4周=7周

LS_E=LF_E-6周=5周

类似地：

LF_A=2周

LF_B=5周

LS_A=0周

LS_B=1周

最早或最迟开始时间可以用于制定项目进度计划。例如，最先开始的活动是A，因为其最迟开始时间为零。否则，该项目将无法在17周之内完成。如果某一项活动的最迟开始时间比最早开始时间大的话，那么这项活动可以安排在最迟开始时间与最早开始时间之间的任意一天进行。例如，对于活动D，它可以安排在第4周与第7周之间的任何时候开始进行，具体时间取决于能否获得资源。所有活动的最早开始时间、最早完成时间、最迟开始时间、最迟完成时间如图16-11所示。

（3）计算松弛时间，确定关键路径。根据各活动的总时差TF计算出松弛时间，可以计算出活动A、C、G、I的时差为0，因此项目Ace的关键路径可以确定为A→C→G→I。