统计过程控制方法在度量产品或服务的当前质量以及检测流程本身是否发生了会影响质量的改变方面十分有用。这里首先讨论计量值变量的控制图,然后再讨论计数值变量的控制图。15.4.3.1 计量值变量的控制图
计量值变量的控制图的管理和控制对象为长度、重量、时间、强度、成分及收缩率等连续量。这里介绍两种计量值变量的控制图,即极差控制图和均值控制图。
1.极差控制图
极差控制图也叫R图,用于检查生产过程中的残差。R图用于监控流程变异。分析人员将每个样本的最大值与最小值相减,即可得到样本数据的极差。如果任一数据落在控制界限之外,则流程变异未得到控制。
R图的控制界限为:
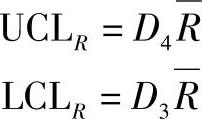
式中,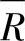 为以往几个R值的平均值,且为控制图的中心线;D3、D4为规定一个给定样本容量的样本处于3倍标准差界限的常数,D3与D4的值可从表15-2中查到,这两个值是样本容量的函数。
为以往几个R值的平均值,且为控制图的中心线;D3、D4为规定一个给定样本容量的样本处于3倍标准差界限的常数,D3与D4的值可从表15-2中查到,这两个值是样本容量的函数。
注意:样本容量越大,控制界限的范围越窄。这一变化是由于有更多的信息可以用来估计流程极差所致。
2.均值控制图
均值控制图又叫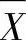 图,用于检查生产过程中的中心变动趋势。
图,用于检查生产过程中的中心变动趋势。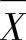 图用于度量均值。当流程变异的可控原因被找到,流程变异处于统计控制之中后,分析人员可以构建
图用于度量均值。当流程变异的可控原因被找到,流程变异处于统计控制之中后,分析人员可以构建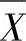 图来控制流程图的均值。
图来控制流程图的均值。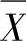 图的控制界限为:
图的控制界限为:
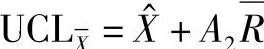
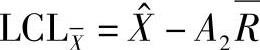
式中,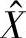 为控制图的中心线,同时或是以往所有样本的平均值,或是流程的目标值集合;A2为规定一个给定样本容量的样本处于3倍标准差界限的常数,A2的值可从表15-2中查到。
为控制图的中心线,同时或是以往所有样本的平均值,或是流程的目标值集合;A2为规定一个给定样本容量的样本处于3倍标准差界限的常数,A2的值可从表15-2中查到。
注意:控制界限用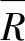 值,因而比较在流程变异处于控制之后方可建
值,因而比较在流程变异处于控制之后方可建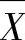 图。
图。
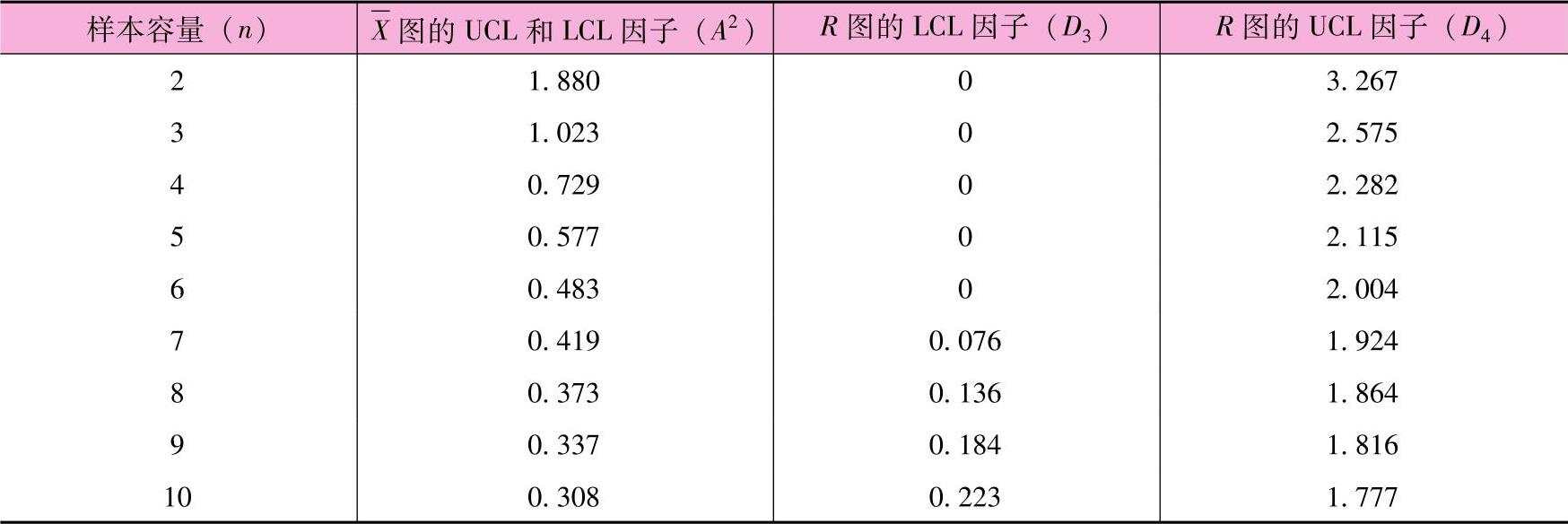
计算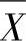 图和R图3倍标准差界限时的影响因子如表15-2所示。
图和R图3倍标准差界限时的影响因子如表15-2所示。
表15-2 计算X图和R图3倍标准差界限时的影响因子
分析人员可以采取以下方式开发、利用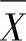 图与R图:
图与R图:
步骤1:收集计量值法测度质量时的数据(如重量、直径、时间),并按照样本数组织这些数据。为了构建一个控制图,最好取20个以上样本。
步骤2:计算每个样本的极差及样本集合的平均极差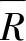 。
。
步骤3:运用表15-2确定R图的控制上限与控制下限。
步骤4:对样本极差描点。如果所有值都处于控制之中,则继续进行步骤5。否则,找出可控原因并纠正,然后返回步骤1。
步骤5:计算每个样本的 值以及图的中心线
值以及图的中心线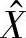 。
。
步骤6:运用表15-2确定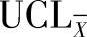 与
与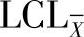 的参数,构建X图。
的参数,构建X图。
步骤7:对样本均值描点。如果所有值都处于控制之中,则流程在流程均值与流程变异方面处于统计控制之中,继续抽取样本并监控流程。如果任何一个值失去控制,则找出可控原因并纠正,然后返回步骤1。如果用心找但仍找不到可控原因,则假设失控点代表的是一般原因变异,继续对流程进行监控。
15.4.3.2 计数值变量的控制图
计数值变量的控制图主要以不合格品数、不合格品率、缺陷数等质量特性来控制产品质量。这里介绍两种计数值变量的控制图——p图与c图。p图与c图是根据产品或服务的计数值变量测度质量的两个常用图。p图用于控制流程产生的缺陷产品或服务的比例;c图用于控制当前产品或服务中出现一个缺陷时的次品数目。
1.p图(www.daowen.com)
p图是计数值变量常用的控制图。质量特征不能连续测度,只能计数。整个产品或服务可以看成要么是好的,要么是差的。例如,在银行业,计数值变量的计数可能是未背书的存款数目或是发出错误金融报表的数目。该方法需要随机选取样本、检查样本中的每一件产品,再计算次品率p,即次品数量除以样本容量。
p图的样本抽样是一个关于是或否的决策:产品或服务要么存在缺陷,要么不存在缺陷。主要的统计分布是二项分布。然而,对较大的样本容量,也可以近似地视为正态分布。次品率的标准差σp为:
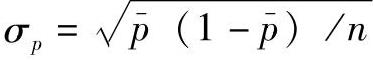
式中,n为样本容量; 为次品率的历史平均值,或设定值及图的中心线。
为次品率的历史平均值,或设定值及图的中心线。
p图的中心线可以是以往样本次品率的平均值,也可以是管理层为该流程设定的一个目标值。我们用σp来算出p图的控制上限和控制下限:
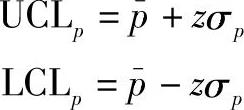
式中,z为一般偏差(平均值的标准差数目)。
可以通过以下几种方式运用此图:定期抽取样本容量为n的随机样本,对缺陷产品或服务的数目计数。次品数除以样本容量得到样本的次品率p,并在图中描点。当一个样本的次品率落在控制界限之外时,分析人员会假定流程产生的次品率发生了变化,并寻找可控原因。观察值落在控制下限的下方,意味着流程实际上可能已经得到了改进。由于总会有较小的机会使“失控”随机发生,因而分析人员可能找不到可控原因。但是如果分析人员发现了可控原因,那么这些样本数据就不应该再用于计算该图的控制界限了。
例15-1:某银行的数据处理部门有四名数据录入员。他们的领导每天进行随机抽查来检验录入的准确度,样本容量为250个记录。含有1个或1个以上错误的记录都认为是有缺陷的,必须重做。最近的30个样本的结果如表15-3所示,全都进行了检查以确保没有一个失控。
表15-3 最近的30个样本的结果
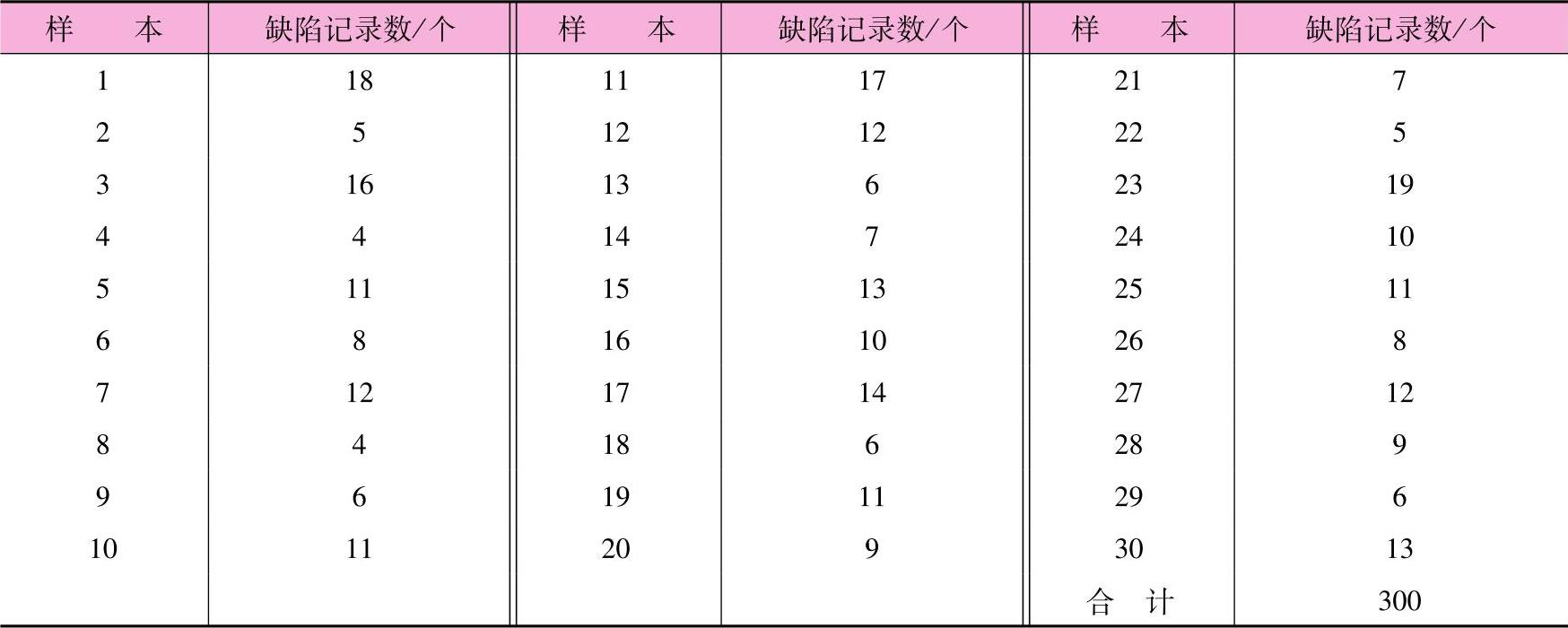
(1)基于这些历史数据,作出z=3时的P图。
(2)接下来4天的样本如表15-4所示。
表15-4 接下来4天的样本

那么,管理者可能会对数据录入过程作出怎样的评价?
(1)根据表15-4,管理者得知7500个(30×250)记录的总样本中缺陷记录数总数为300个。因此,图的中心线为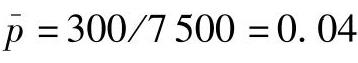
控制界限为: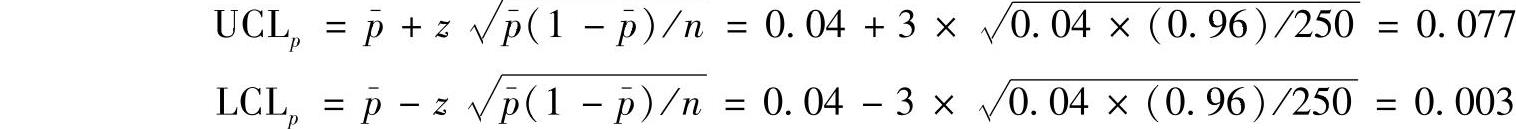
(2)接下来4天的样本如表15-5所示。
表15-5 接下来4天的样本

样本33与34失去控制。管理者应该寻找问题所在,并在此基础上采取纠正行动。
2.c图
c图用于控制一部机器、一个部件一定的长度、一定的面积或任一一定的单位中所出现的缺陷数目。有时候一件产品会存在一个以上的缺陷。例如,一卷地毯可能存在几个缺陷,如在生产过程中产生的脱色、纤维起毛或污点。当管理层对降低单位缺陷数感兴趣时,另一种控制图c图就有用了。
c图的主要分布是泊松分布。该分布假设缺陷发生在一个连续区域,同时任何一个地点发生两个或两个以上的缺陷的概率可以忽略不计。
该分布的均值为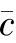 ,标准差为
,标准差为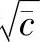 。可以将这个泊松分布用正态分布近似表示,这样图中的中心线就是
。可以将这个泊松分布用正态分布近似表示,这样图中的中心线就是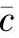 ,控制界限则为:
,控制界限则为:
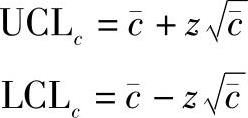
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







