工作抽样创始于1934年，由英国统计学者迪佩特（L.H.Tippett）首先应用统计学与概率论原理，在纺织厂中用来调查织布机的开动率和工时利用率，并将其研究成果公开发表，命名为快读法（Snap-Reading Method）。由于当时人们对数理统计知道得很少，论文没有引起反响。1940年美国动作研究专家莫罗（R.L.Morrow）将此法用来测定正常作业时间应加上多大宽放率，并称之为比例延迟法（Rati-o-Delay Study）。随后动作研究专家巴恩斯（R.M.Barnes）亦开始了对此法的研究，并将部分有关论文编辑成册出版，书名为《工作抽样》（Work Sampling）。在此著作中，介绍了工作抽样的基本原理和大量的应用实例。从此，工作抽样才逐渐为人们所认识和接受，并成为应用十分广泛的工作研究技术，成功地应用于工厂、医院、商店、学校、银行及政府机关等单位。

顾名思义，工作抽样涉及工作活动的一部分或工作活动的样本。然后，基于对这个样本的发现，可以对活动作出描述。例如，如果我们观测一个消防部门中的营救小组，一天中随机观测100次，发现在100次观测中它从事营救工作的次数为30次（无论在途中、在事故地点还是在返回），那么可以估计出，该营救小组30%的时间直接花在营救任务上。观测的时间取决于观测的对象。很多时候只需要几秒钟的观测时间就可以确定对象的状态。

然而，对某一活动即便是观测了100次，也未必能够保证估计达到所要求的准确度。为了对这种估计进行改善，必须确定如下三个问题：

（1）要求结果中统计的置信度水平是多少？

（2）必须作多少次观测？

（3）精确地知道应何时作出观测。

工作抽样有以下三个主要应用：

（1）用等待所占的时间百分比来确定人或设备的工作时间百分比。例如，管理者可能对机器的运行或闲置时间比较感兴趣。

（2）用作业水平测定可以为每个工人的表现建立一个指数，当工作的时间和产出的数量相关时，就须对作业水平进行测定。

（3）用时间标准来确定一项任务的标准时间。然而，当工作抽样是为了达到这个目的时，观测者必须富有经验，因为他也必须与时间研究类似地为观测值确定一个作业比率。

工作抽样研究中所需要的观测次数从几百次到几千次不等，这主要取决于活动和所要求的精度等级。虽然这些数据可以通过运用公式计算而得到，但最简单的方法是从表中查取。表13-8中给出了绝对误差的置信度为95%时所需要的观测次数。绝对误差是观测的实际范围。例如，如果一个办事员的闲置时间为10%，该研究的设计者对2.5%的波动范围比较满意（即真正的百分比在7.5%～12.5%之间），则工作抽样所要求的观测次数就为576次。如果要求2%的误差（即在8%～12%之间），则要求观测的次数为900次。

表13-8 对于给定的各种不同的绝对误差值P在置信度为95%时要求的观测次数

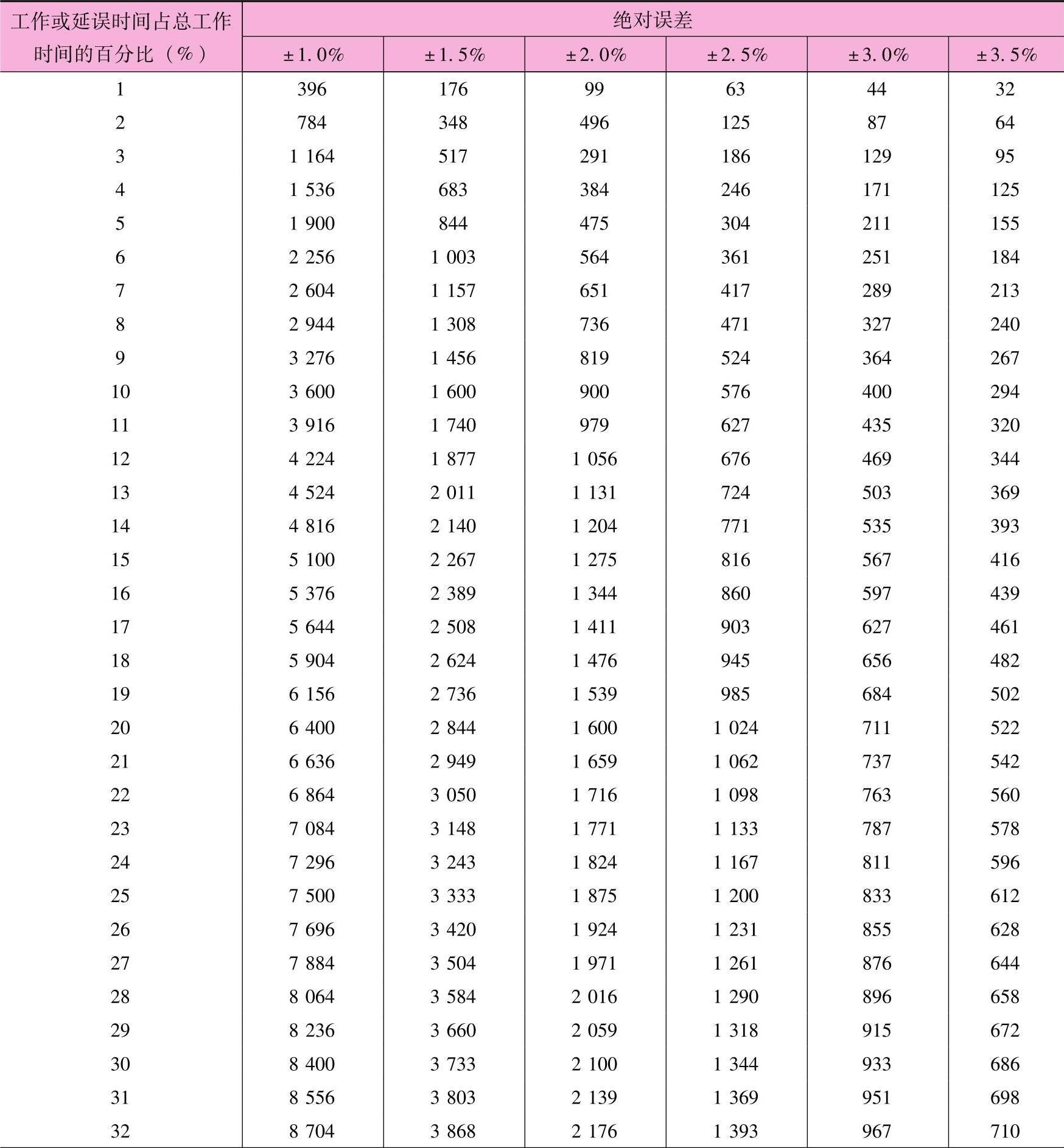
（续）

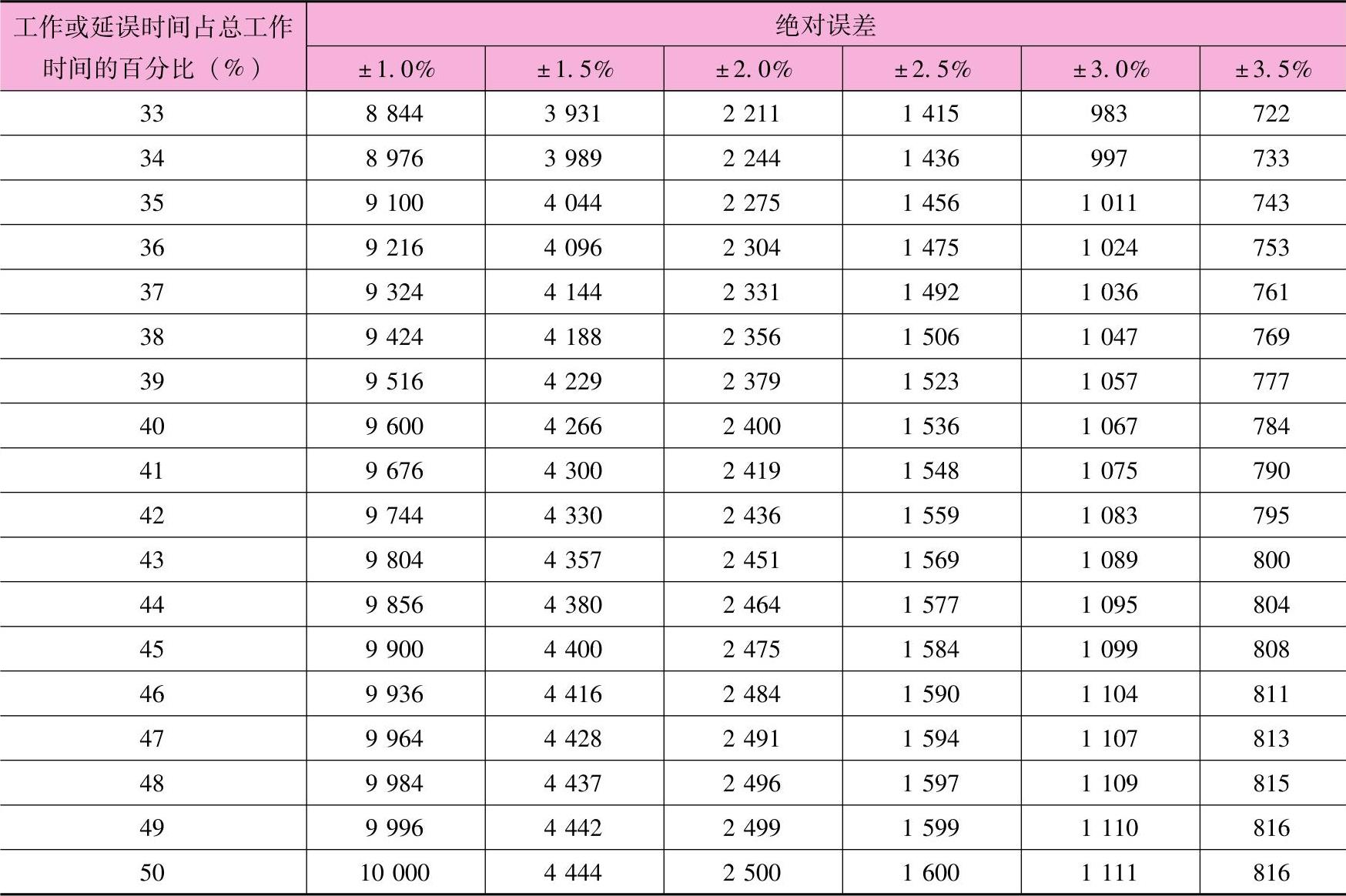
工作抽样研究涉及如下五个步骤：

（1）识别特定的活动，这些活动是研究的主要目的。例如，确定设备工作、闲置和维修时间各自所占的百分比。

（2）估计对整个系统有利害关系的活动占活动总时间的比例（例如，设备运行时间为80%）。这些估计可根据分析人员的背景知识、以前的数据、其他人的可靠猜测或从一个探索性的工作抽样研究中得到。

（3）给出研究结果所要求的精确度。

（4）确定进行每一次观测的特定时间。

（5）在研究期间，每隔两次或三次，用目前所收集到的数据重新计算所要求的样本容量，如果必要就提高观测的次数。

工作抽样研究中的观测次数在整个研究期间通常被均分成几个部分。因而，如果10天内要观测500次，则观测计划通常定为每天观测500/10次，即每天50次。每天的观测通过使用一个随机数表分配特定的观测时间。(www.daowen.com)

观测次数由下列公式确定：

需要的样本数

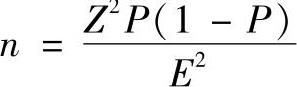
式中，E为绝对误差；P为观测的工作或延迟发生的概率；n为随机观测次数；σ为抽样的标准差；Z为给出所要求置信度的标准偏差值（置信度为90%，Z=1.65；置信度为95%，Z=1.96；置信度为99%，Z=2.23）。

例13-2：工作抽样在护士工作中的应用。长期以来一直存在着这样一种争论：护士在医院的很大一部分时间消耗在非护理活动上。这种争论认为，这明显不能发挥经过优良培训的护士的长处，浪费了人才，阻碍了工作的效率，并且增加了医院的成本。基于这一点，让我们用工作抽样理论来验证护士的很大一部分时间消耗在非护理活动上这一假说。

首先假设我们已经列出了一系列作为护理工作的组成部分的活动，我们把观测结果分为两类：护理活动和非护理活动。实际上，在护理活动的组成这个问题上存在着很大的争议。例如，与病人谈话是否属于护士的护理活动的范围？深入的研究中可列出所有的护理活动，以确定每次观测中花费在护理活动上的时间所占的比例。因此，在研究期间，当观测并发现护士所要执行的任务属于护理活动时，只需在护理活动这一栏上作一个标记。如果所观测的不属于护理活动，则在非护理活动这一栏上作一个标记。

现在我们可以继续计划这项研究。假定我们估计护士60%的时间花在护理活动上，并假定我们的置信度为95%，研究结果的绝对误差的范围为±3%，即如果我们的研究显示护士60%的时间花在护理活动上，置信度为95%时，真正的百分比范围应该在57%～63%。从表13-8中可以查出在工作时间为60%，误差范围为±3%时，所需要的观测次数为1067次。如果该研究要用10天时间，那么每天需要观测107次。

为了确定每天何时进行观测，我们把一些特定的数字分配给每一分钟并且用一个随机数表来建立一个进度表。在这项研究中，晚班需要单独地进行研究，因为晚班护士的职责与白班护士的职责存在很大的不同。表13-9中给出了为每一分钟所分配的相应的随机数。因为每一个数字对应于每一分钟，为了简化，可以采用三位数字计划编制法。其第二位和第三位数字对应于该小时中相应的每一分钟。也可采用其他的计划方法。如果计划要进行许多次研究，则可以使用计算机程序来产生一个随机的计划表以确定观测的时间。

表13-9 护士活动的抽样计划

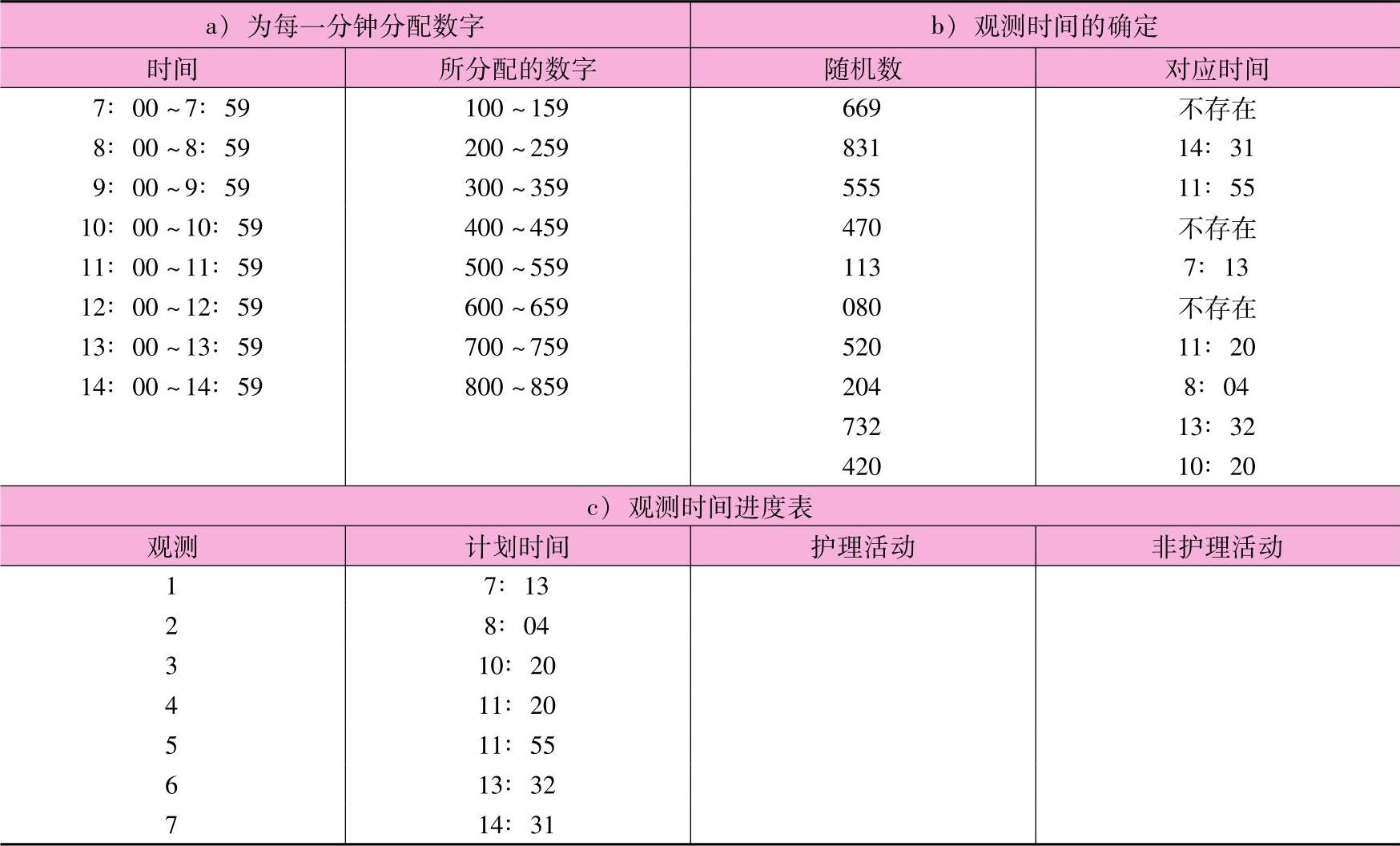
如果我们参考一个随机数表并将三位数字列成表，则可以为每一数字分配一个时刻。表13-9中的随机数字说明了7次观测的程序。依照这个程序要产生107次观测的时间，为了使计划简化，这些时间要按时间顺序重新整理。表13-9中所确定的时间经过重新整理后，形成每天全部观测的时间（样本中只有7次观测）。

为了使这项研究更具有随机性，应使每一次观测哪一位护士也具有随机性（观测不同的护士可使偏差达到最小）。在该项研究中，第一次观测是在上午7∶13对护士X进行观测。我们走到护士工作的地方，看所要观测的那位护士是在做护理工作还是非护理工作。每一次观测时间的长短只需判断该活动属于哪一类即可。在大多数情况下只需要看一眼就可以了。上午8∶04，我们观测护士Y。以这种方法进行了107次观测，直到这一天结束为止。在第二天结束时（已经观测了214次），要核实样本的容量是否足够。

假定我们对护士的工作进行了214次观测，其中有64次她们所做的工作属于非护理活动，即护理活动只为70.1%。由表13-8可知，这对应于933次观测。因为我们已经观测了214次，以后只要在8天中进行719次观测，即每天只要观测90次即可。

当该研究进行到第5天结束时，我们需要再作一次检验。例如，如果第3、4和5天中观测到的护理活动次数分别为55、59和64次，那么在484次观测中，属护理活动的有328次，护理活动占67.8%。

如果误差为±3%，从表13-8可知，样本容量应约为967次，剩下483次观测要在剩下的5天内完成，即每天要完成的观测次数为97次，在第9天结束时应再计算一次，看是否需要再进行调整，如果第10天后，还需再观测几次，那么还应继续在第11天中进行观测。

如果该研究结束时，发现护士有66%的时间花在我们所定义的护理活动中，那么应该有分析人员对剩下的34%的时间进行鉴定。大约12%～15%是有正当理由的：喝咖啡的中断或个人的生理需要，剩下20%～22%的时间需要同医院所认为的理想的护理活动进行比较，并且证明这部分时间是有正当理由的。为了识别非护理活动，需要把更加详细的分解列入抽样计划中，否则必须进行更加深入的研究。

如前文所提到的那样，工作抽样可用于设定时间标准，为此，分析人员在对工作进行观测的同时必须记录对象的作业比率（或者指数）。表13-10给出了一个生产中的实例，其中说明了如何应用工作抽样来计算标准时间。

表13-10 用工作抽样导出时间标准