首先，我们在一个静态的情景中比较一下8个优先级规则中的部分规则。在这个情景里，我们对同一机器上的5项作业进行排序（在排序术语中，这类问题被称为“N项作业单机问题”或者简称为“N/l”）。理论上，排序问题的难度随着考虑的机器数量增加而增加，而不是随任务数量的增加而增加。因此，对于N的唯一限制，就是N必须是一个特定的、有限的值。

例12-1：一家公司为市中心的法律公司提供复印服务。5个顾客在每周开始的时候下订单。计划数据如表12-3所示。

表12-3 计划数据

所有这些作业都要使用唯一可用的彩色复印机。请决策5个订单的处理顺序（评价标准是流程时间最小化）。

（1）FCFS规则。采用FCFS规则得到的流程时间如表12-4所示。

表12-4 FCFS计划

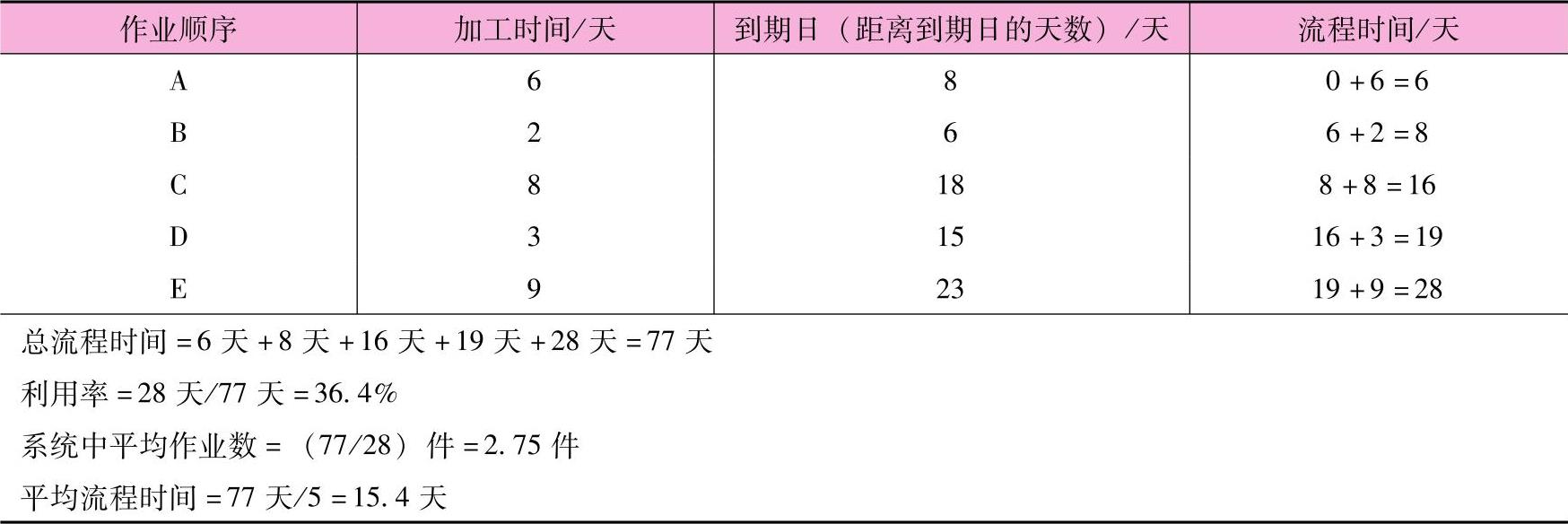
将每项作业的流程时间和到期日作比较，我们发现只有作业A、C可以准时完成。作业B、D和E分别会延迟2、4、5天。平均一个作业会延迟2.2天（（0+2+0+4+5）/5）。

（2）SOT规则。现在考虑SOT规则。这里把最高优先级给加工时间最短的订单。得到的流程时间如表12-5所示。

表12-5 SOT计划

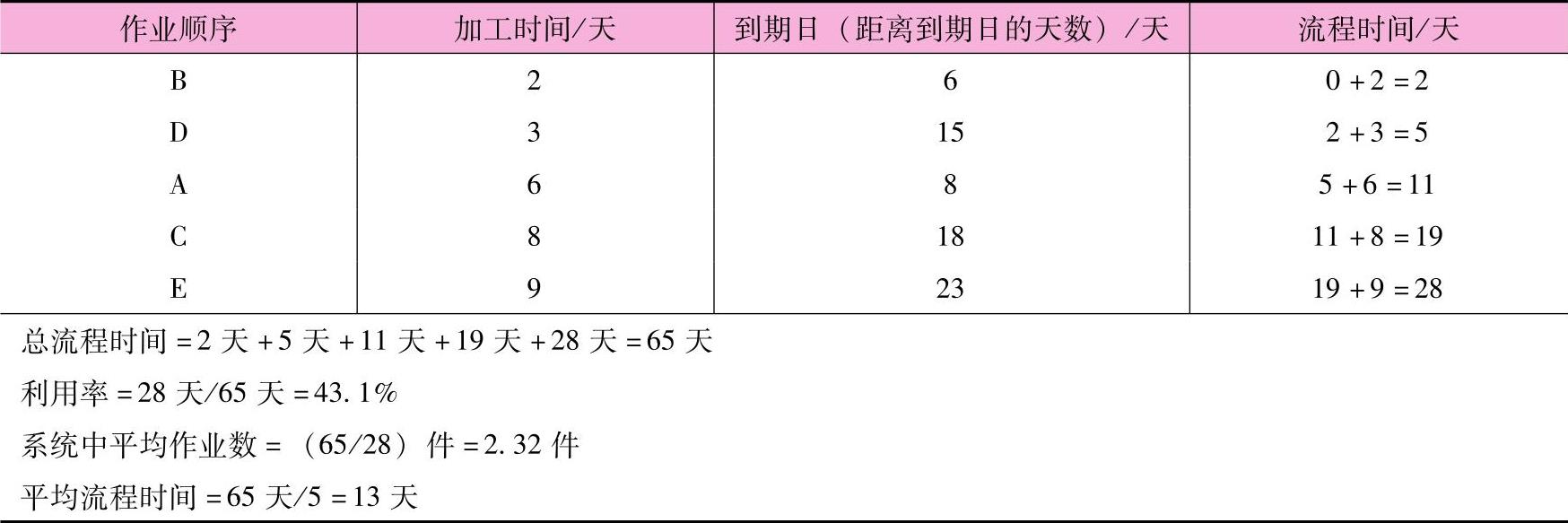
SOT得出的平均流程时间比FCFS得出的要短。此外，作业B和D在到期日之前可以交货，作业C只延迟一天。作业平均延迟时间为1.8天（（0+0+3+1+5）/5）。(www.daowen.com)

（3）EDD规则。如果采用EDD规则，则得到的流程时间如表12-6所示。

表12-6 EDD计划

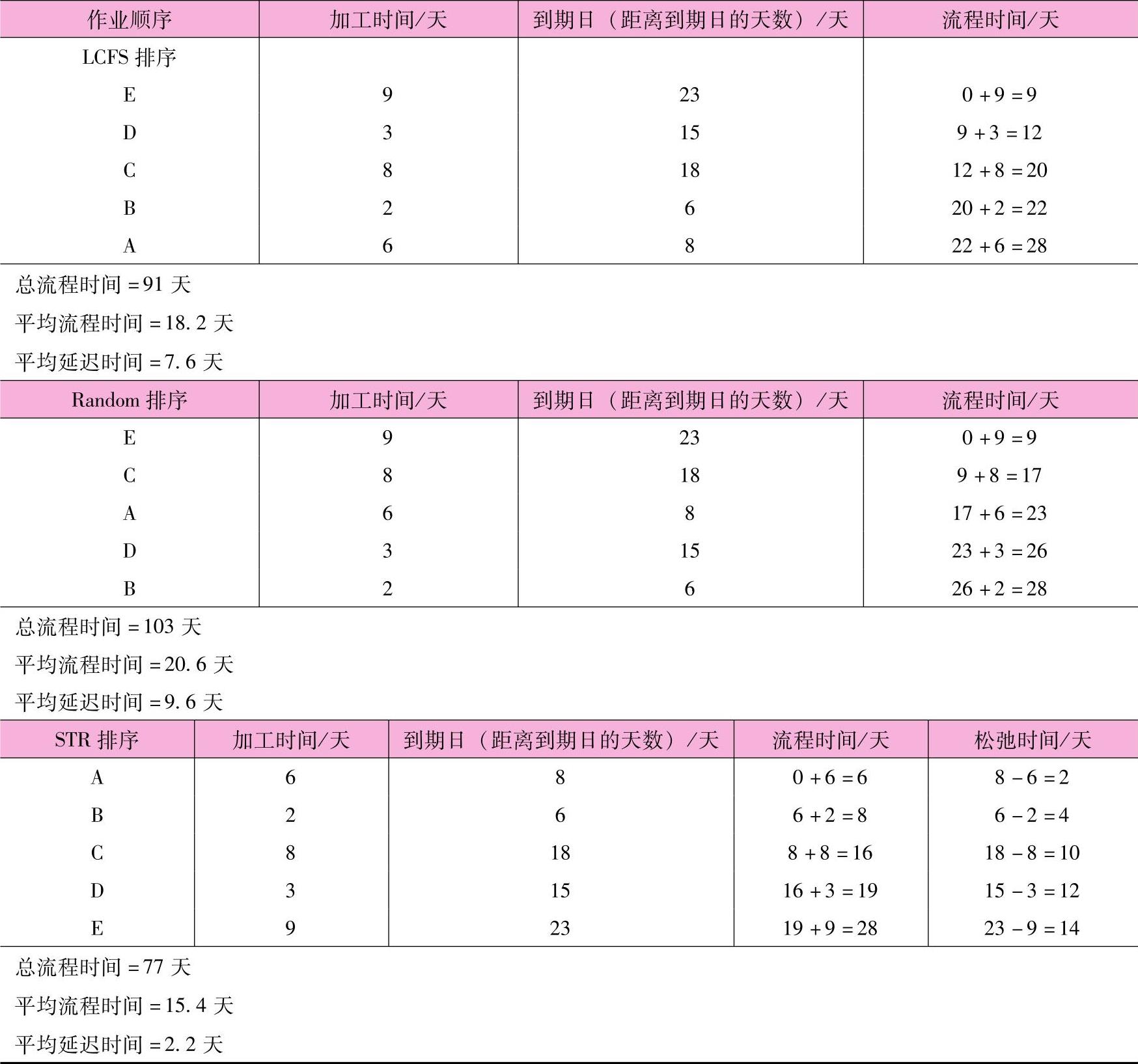
这种情况下，作业C和E会延迟。平均每个作业延迟1.2天（（0+0+0+1+5）/5）。（4）LCFS、Random和STR规则。LCFS、Random和STR规则得到的流程时间如表12-7所示。

表12-7 LCFS、Random和STR规则得到的流程时间

各种规则下的结果汇总如表12-8所示。

表12-8 各种规则下的结果汇总

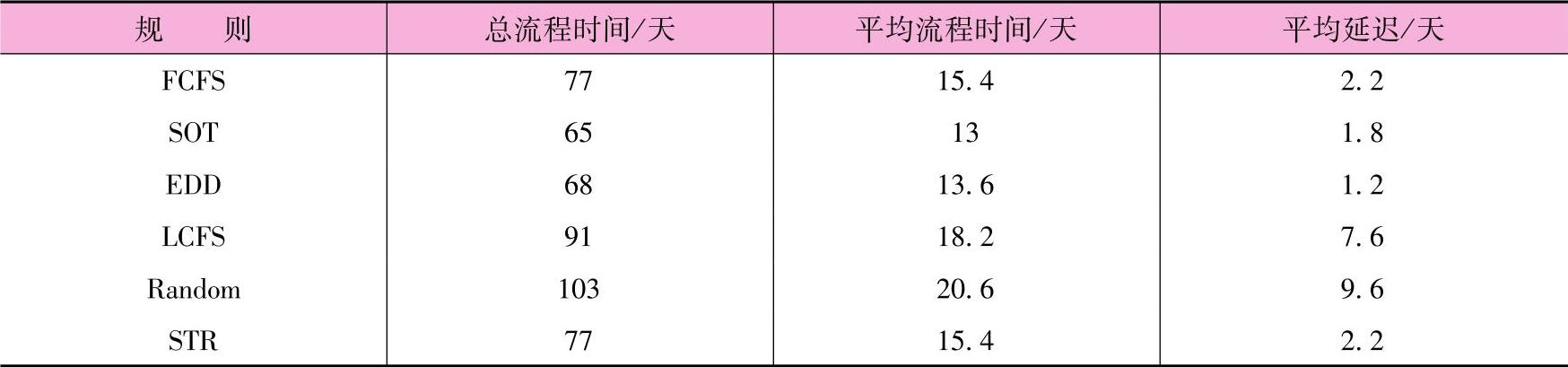
从流程时间角度来看，SOT比其他的规则要好。此外，计算显示在N/l的情况下，SOT可以获得平均等待时间最短的解决方案。这个简单的规则就是这么具有威力，以至于被誉为“排序方面最重要的概念”。但它也有缺点。最主要的就是耗时短的任务不断到达致使耗时长的任务一直不能开始。为避免这种情况的发生，公司通常会采用截取SOT规则（atruncatedSOT规则），在这种规则中作业等待时间一旦达到特定值，就会自动移到等待队列的前面。

此外，相对于SOT，EDD在本例中可以获得平均延迟最短的解决方案，在实际工作中可以根据不同的指标要求选择不同的规则用以排序。