【摘要】：反复试验法又称图表法。由于制定综合计划涉及的因素非常复杂，寻求最优的综合计划比较困难，因此人们常常应用反复试验法求出满意的综合计划。线性规划法是以综合计划中总成本最小化为目标。通过建立相应的线性规划模型，可以获得最优综合计划的解决方案。表10-5 某厂生产及经营数据可采用线性规划法确定每个品种的最佳产量。
通常，制定综合计划时主要有反复试验法及数学模型法（以线性规划法为主）。
（1）反复试验法。反复试验法又称图表法。在利用此方法制定计划时，通常一次只考虑少数几个变量，这有助于计划制定者对现有能力与预期需求进行比较。它通过反复试验与纠错来选定方案，但不能保证得到最佳生产计划。此方法只进行有限的计算，可由普通办公室文员完成。由于制定综合计划涉及的因素非常复杂，寻求最优的综合计划比较困难，因此人们常常应用反复试验法求出满意的综合计划。
（2）线性规划法。线性规划法是以综合计划中总成本最小化为目标。总成本包括正常工作时间、加班时间、转包单位费用、存货库存成本以及改变劳动力水平的相关成本等，约束条件为劳动力数量、工作时间、存货和转包能力等。通过建立相应的线性规划模型，可以获得最优综合计划的解决方案。
表10-4总结了反复试验法和线性规划法的一些主要特征。
表10-4 两种主要综合计划编制方法总结
例10-2：某公司生产A、B、C、D四种产品，各产品需要经过车、钻、装配、检验等工序，生产及经营数据如表10-5所示。试建立其生产计划的线性规划模型。
表10-5 某厂生产及经营数据
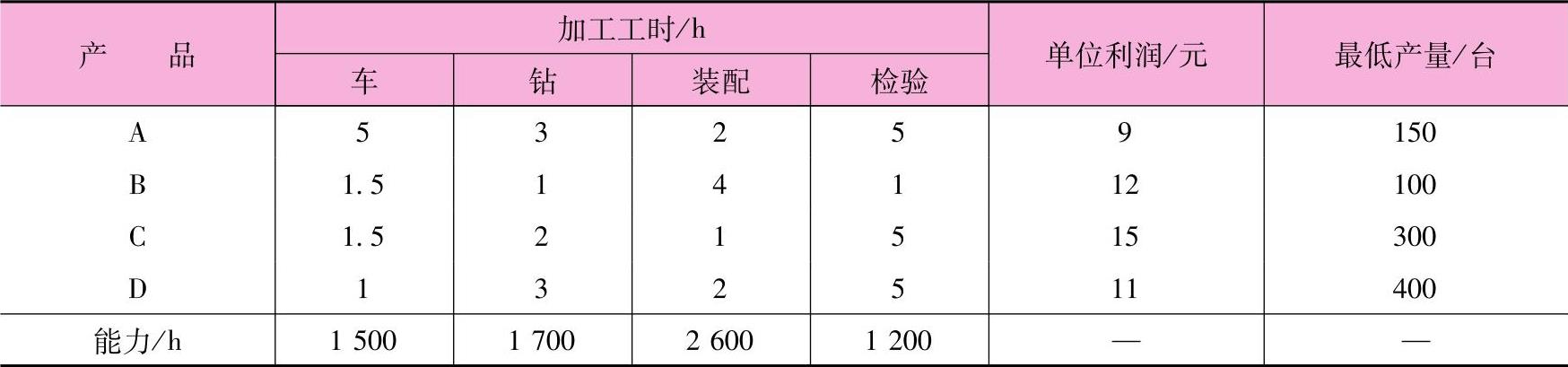
可采用线性规划法确定每个品种的最佳产量。
确定变量：设X1、X2、X3、X4分别为A、B、C、D四种产品的生产数量。
目标函数：(www.daowen.com)
Zmax=9X1+12X2+15X3+11X4
约束条件：
5X1+1.5X2+1.5X3+X4≤1500
3X1+X2+2X3+3X4≤1700
2X1+4X2+X3+2X4≤2600
5X1+X2+5X3+5X4≤1200
X1≥150
X2≥100
X3≥300
X4≥400
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
