时间序列预测法是依据数理统计中的回归分析理论和方法，将需求作为因变量，将时间作为唯一的独立变量，建立预测目标与影响因素之间关系的数学模型，并据此进行预测的方法。这种做法虽然简单，但忽略了其他影响需求的因素，如政府部门公布的各种经济指数、地方政府的规划、银行发布的各种金融方面的信息、广告费的支出、产品和服务的定价等，都会对需求产生影响。因果模型则有效地克服了时间序列预测法的这一缺点，它通过对一些需求（如书包）有关的先导指数（学龄儿童数）的计算，来对需求进行预测。在社会经济现象之间，因果关系大致可分为函数关系、相关关系、因子推演关系等几种不同的类型。由于反映需求及其影响因素之间因果关系的数学模型不同，因果模型又分为回归模型、经济计量模型、投入产出模型等。

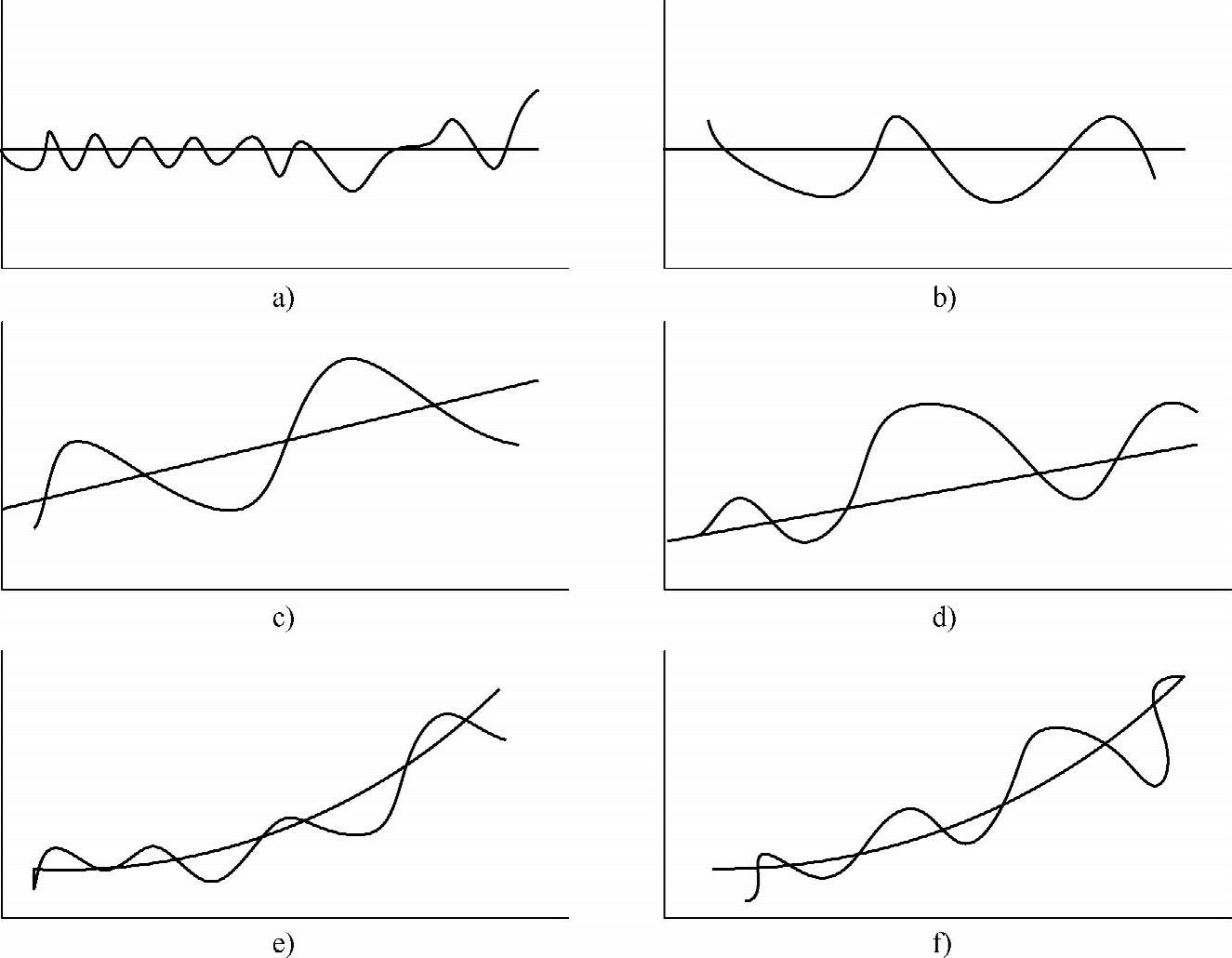
图9-2 几种可能的时间序列类型

a）无趋势，无季节波动 b）无趋势，有季节波动 c）线性趋势，相等的季节波动 d）线性趋势，增大的季节波动 e）非线性趋势，相等的季节波动 f）非线性趋势，增大的季节波动

一元线性回归分析预测法是分析一个因变量和一个自变量的关系的一种方法。影响市场变动的因素是多方面的，如果其中的一个因素是主要的和起决定作用的，而且其自变量与因变量之间的数据分析呈线性趋势，就可以用一元线性回归方程进行预测。原因分为必要原因和充分原因。

所谓必要原因，是指现象Y的发生（变化）一定要以现象X的发生（变化）为前提，因此X被认为是Y的必要原因。换言之，如果X不存在，那么Y必定不会存在。例如，氧元素的存在是燃烧的必要条件，也就是说，一旦不存在氧，也就不存在燃烧。必要原因的特点是能从一个现象（果）的存在确定性地倒推回另一个现象（因）的存在。例如，如果取得博士学位是获得教授职称的必要条件，那么一旦观察到某人获得了教授职称，就肯定可以判断他之前取得了博士学位。所谓充分原因，是指现象X的发生（变化）一定会导致现象Y的发生（变化）。例如，在一定大气条件下，气温下降到0℃，水一定会变成冰，因此0℃以下的温度是水变成冰的充分原因。

使用该法，首先要分清因果地位。其次要注意因果对应。任何结果都由一定的原因引起，一定的原因产生一定的结果，因果常是一一对应的，不能混淆；最后，要从不同的方向用不同的思维方式去进行因果分析，这也有利于发展多向思维。因果预测分析是整个预测分析的基础。因果分析法（技术）运用于项目管理中，就是以结果作为特性，以原因作为因素，逐步深入研究和讨论项目目前存在问题的方法。因果分析法的可交付成果就是因果分析图。一旦确定了因果分析图，项目团队就应该对之进行解释说明，通过数据统计分析、测试、收集有关问题的更多数据或与客户沟通来确认最基本的原因。确认了基本原因之后，项目团队就可以开始制定解决方案并进行改进了。

1.应用步骤

因果分析法预测的基本思路是：首先，通过对市场经济现象之间因果关系的分析探讨，说明现象之间相互联系的规律性；其次，选择恰当的数学模型描述因果关系主要变量间的关系形态；最后，根据数学模型预测市场发展前景及可能达到的水平。

因果分析法的应用步骤大致如下：

（1）利用资料分析市场现象之间的因果关系，确定预测目标以及因变量和自变量。分析市场现象因果关系必须做到：①凭人们所拥有的经验、知识以及思维判断能力，对预测问题在质的分析基础上，明确表征预测目标的运动规律及影响其变化的因素的诸多市场变量；②选定因变量和自变量。

通常情况下：表征预测目标的变量称因变量（如卷烟零售量或零售额）；表征影响预测目标变化的各种因素的变量称自变量。

从市场预测过程来讲，明确预测目标选定因变量是首要任务，但能从众多影响预测目标的因素中选定参与预测的自变量，是保证预测结果可信度的关键。

（2）根据变量之间的因果关系类型，选择数学模型，并经过运算，求出有关参数，通过统计检验建立预测模型。

（3）预测分析，确定预测值。市场的客观经济现象是十分复杂的，数学预测模型只能明确、形象地显示出市场从过去至现在发展过程中有关事件观察数据中呈现的因果关系，而如何确定符合市场需要及其变化客观实际的预测值，还需要预测者掌握丰富的市场信息，依靠个人的经验和分析判断能力，最后作出科学判断。

运用量的分析的因果分析法进行市场预测时，还需要与质的分析相结合，把各种主要因素考虑进去，参照已经出现和正在出现的可能性，综合分析判断，对预测模型计算出来的预测值作恰当调整，确定最终预测值，使预测结果更接近实际。

2.因果关系类型

因果关系大致可分为函数关系、相关关系、因子推演关系等几种不同的类型。

（1）函数关系。函数关系是指几种社会经济现象之间存在确定的数量关系。在预测具有此种函数关系的经济事物时，常用的方法有直线回归模型、二次曲线模型、指数曲线模型等。

（2）相关关系。相关关系是指两种或两种以上的社会经济现象间存在着相互依存关系，但在数量上没有确定的对应关系。在这种关系中，对于自变量的每一个值，因变量都可以有几个数值与之相对应，表现出一定的波动性、随机性，但又总是围绕着它们的平均数并遵循着一定规律而变动。相关关系与函数关系是性质不同的两类变量间的关系。变量之间存在着确定性数量对应规律的称为函数关系，可以用数学函数式表达。变量间不存在确定性数量对应规律的要用统计学的方法来研究。统计学上研究有关社会经济现象之间相互依存关系的密切程度，相关分析可以得到一个表明相关程度的指标，称为相关系数。这种方法对于不能在实验室用实验方法分析的社会经济现象显得特别重要。通过相关分析，还可以测定和控制预测的误差，掌握预测结果的可靠程度，把误差控制在一个范围内。(www.daowen.com)

社会经济现象之间的相互关系是非常复杂的，表现出不同的类型和形态。从变量之间相互关系的方向来看，分为正相关和负相关。在某些经济现象之间，当自变量x的值增加时，因变量y的值也随之相应地增加，这样的相关关系就是正相关。当自变量x的值增加时，因变量y的值随之而呈减少的趋势，这种关系就是负相关。

从变量之间相互关系的表现形式来看，可分为直线相关与非直线相关。当x值发生变动时，y值随之发生大致均等的变动（增加或减少），表现在图形上，其观察点分布于狭长的带形区域之内，并近似地表现为直线形式，这样的关系通称为直线关系。当x值变动时，y值随之呈不均等变动（增加或减少），表现在图形上，其观察点的分布近似地表现为各种不同的曲线形式，这种相关关系通称为非直线相关。相关关系中重要的是判断变量的相关系数。

（3）因子推演关系。因子推演关系就是根据引起某种社会经济现象变化的因子，来推测某种现象的变化趋势。例如，每年新建立的家庭数目是住房需要量的因子；青年结婚的数量是家具和衣服的销售量的因子；婴儿出生人数是玩具需要量的因子；汽车销售量是汽车配件需求量的因子等。根据某经济现象的因子就可以预测它的需求量变化趋势。

3.方法

因果分析法，是从事物变化的因果关系质的规定性出发，用统计方法寻求市场变量之间依存关系的数量变化函数表达式的一类预测方法。这类预测方法，在市场预测中常用的有两种：

（1）回归分析法。当预测目标变量（因变量）由于一种或几种影响因素变量（自变量）的变化而发生变化时，根据某一个自变量或几个自变量的变动，来解释推测因变量变动的方向和程度，常用回归分析法建立数学模型。

回归分析法是在掌握大量观察数据的基础上，利用数理统计方法建立因变量与自变量之间的回归关系函数表达式，来描述它们之间数量上的平均变化关系。这种函数表达式称为回归方程式。

回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

回归分析中，依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

线性回归分析是最基本的方法，也是市场预测中的一种重要预测方法。

下面介绍一元线性回归模型预测方法。

一元线性回归模型可用下式表达：

式中，Y_t为一元线性回归预测值；a为截距，为自变量x=0时的预测值；b为斜率；n为变量数；X为自变量的取值。

（2）经济计量法。在市场经济条件下，市场作为社会经济活动的基本场所，它一方面是企业营销活动的环境，另一方面也将社会经济系统视为其环境。这种市场现象间的系统关系，使市场变量间的某些因果关系不能只研究自变量对因变量的影响，而忽视因变量对自变量的逆向影响或各种自变量之间的相互影响。

这样一种市场变量间相互依存的复杂关系，回归分析法往往不能对其作出系统描述。

经济计量法就是揭示这类市场变量间复杂因果关系的数量变化关系的方法。

经济计量法，是在以经济理论和事实为依据的定性分析基础上，利用数理统计方法建立一组联立方程式，来描述预测目标与相关变量之间经济行为结构的动态变化关系。这组联立方程式称为经济计量模型。