时间序列是指将某种变量的数值依发生的先后顺序以及按一定的时间间隔排列起来的序列。这些数值可能是产量、利润、销售量、收入，也有可能是运量、事故数等。在此需特别指出的是：每天、每周或每月的销售量按时间的先后所构成的序列，是时间序列的典型例子。常规上，时间序列可以分解成趋势、季节、周期、随机四种成分，如图9-1所示。

（1）趋势成分。数据随着时间的变化表现出一种趋向。它按某种规则稳步地上升或下降，或停留在某一水平。

（2）季节成分。其一年内的变化按通常的频率围绕趋势作上下有规律的波动。

（3）周期成分。在较长的时间里（一年以上）呈现一定的经济周期，以及围绕趋势作有规律的上下波动。一般通过数十年的数据才能描绘出这种周期，并且它是可以没有固定的周期的。

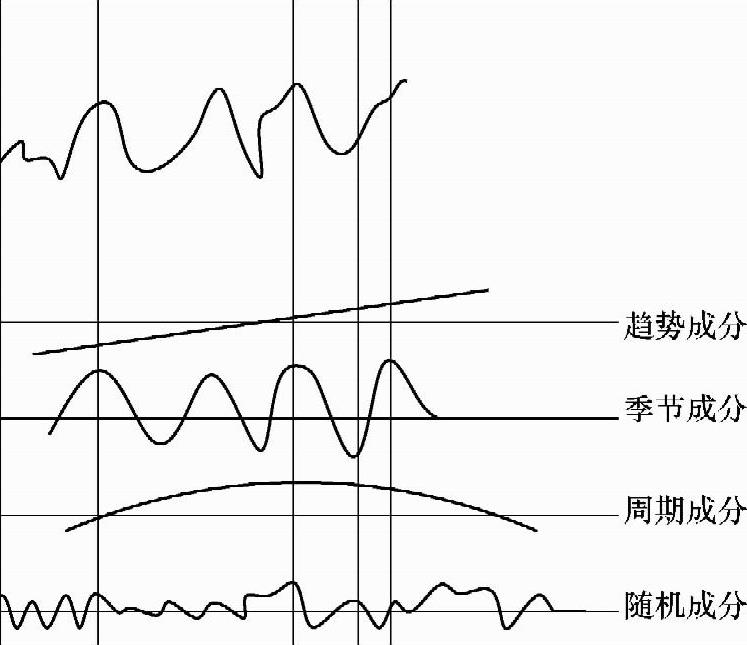
图9-1 时间序列及其构成

（4）随机成分。随机成分是指由很多不可控因素引起的、没有规则的上下波动。

由于随机成分构成的影响是无法预测的，在此就不再讲。而周期成分也需要长期的历史数据作为依托，耗时太久，故在此也不再提起。虽然除去周期和随机成分的影响不作考虑，这也不能影响大部分生产经营决策的科学性。这是因为生产经营决策的时间往往比较短，就算有周期成分，其造成的影响也不会很明显。即使对于长期预测而言，预测也是滚动的，是随着时间的推移而不断修改的，因而周期成分的影响也很小。

x（t₁），x（t₂），…，x（t_n）中自变量t可以具有不同的物理意义，如长度、温度或其他物理量等。时间序列的波动是许多因素共同作用的结果。各种因素作用的效果有长期趋势、季节变动、循环变动和随机变动四类。若以T、S、C、I分别表示长期趋势、季节变动、循环变动和随机变动的数值，那么对时间序列y_t的分析最常用的模型有两类：

y_t=TSCI

y_t=T+S+C+I

9.3.1.1 时间序列平滑模型

时间序列平滑模型往往用在当受随机成分的影响而导致需求偏离平均水平时，通过对多起观测数据平均的办法，可以有效地消除或减少随机成分的影响，使预测结果较好地反映平均需求水平。这里将讨论简单移动平均（Simple Moving Average）、加权移动平均（Weighted Moving Average）、指数平滑等几种时间序列平滑模型。

1.简单移动平均

简单移动平均值可按下列公式计算：

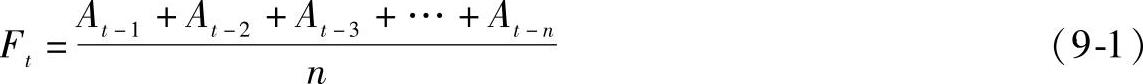
式中，F为t周期末的简单移动平均值，它可以作为t+1周期的预测值；A_i为i周期的实际需求；n为移动平均采用的周期数。

例9-1：某企业1～11月的销售收入时间序列如表9-1所示。取n=4，试用简单移动平均法预测第12月的销售收入。

表9-1 销售收入时间序列

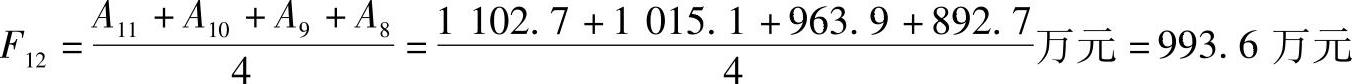
此为第12月份销售收入的预测值。

简单移动平均法，是把参与平均的数据在预测中所起的作用同等对待，但参与平均的各期数据所起的作用往往是不同的。为此，需要采用加权移动平均法进行预测。加权一次移动平均预测法是其中比较简单的一种。

2.加权移动平均

加权移动平均值可按下式计算：

F_t=α₁A_t-1+α₂A_t-2+…+α_nA_t-n （9-2）

式中，F_t为t周期末加权移动平均值，它可以作为t+1周期的预测值；α₁，α₂，…，α_n，为实际需求的权数，且α₁+α₂+…+α_n=1；其余符号意义同简单移动平均法。

显然，若对每个时段的α_i都取相同的值，即同等地对待序列中的每个值，则加权移动平均值就变成了简单移动平均值。因而，简单移动平均是加权移动平均的一种特殊情况。

需要说明的是，所选的周期数越大，预测值对波动的敏感性越低，预测的稳定性越好，响应性就越差。另外，简单移动平均法对数据不分远近，同样对待。但是，实际生活中往往最近的数据反映了需求的趋势，为最近的数据设置较大权重的加权移动平均法更加适用。因此实际操作中方法及参数的选择要根据预测的实践灵活决定。

移动平均法的实质仍然是一种加权平均的方法，它对使用数据给予了相等的权数，即对截距以前的数据给予的权数是零。这种将远期数据截掉不考虑，并把截距中使用的数据同等对待的做法，显然不能完全合理地反映出数据变化的规律。为克服移动平均法的缺点，引出了指数平滑法。

例9-2：仍以例9-1为例，取n=3，并取α₁=1/2，α₂=1/3，α₃=1/6试用加权一次移动平均法预测12月份的销量。

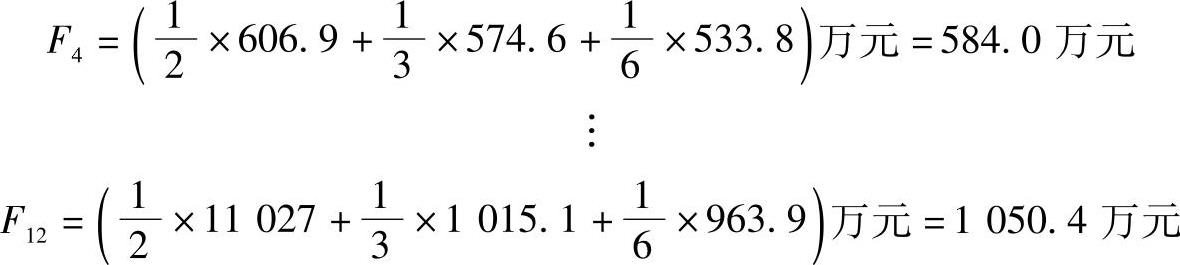
3.指数平滑法

指数平滑法（Exponential Smoothing，ES）是布朗（Robert G.Brown）所提出的。布朗认为，时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续到未来，所以将较大的权数放在最近的资料。这是通过对整个时间序列分别给予不同的权数，而进行加权平均的一种方法。模型建立的原则是：重视近期数据影响，但也不忽视远期数据作用，从而提高了预测精度。

指数平滑法是最常用的预测方法之一，属于确定性的时间序列分析技术。

应当指出，指数平滑法的本质仍然是一种平均方法。所谓滞后现象，是指同期预测值落后于同期实际值。例如，某序列有三个数，2.5、3.0、3.5，则平均值为3.0，即中位数，显然其值小于近期的值3.5，如果此偏差较大，则该方法便失去了使用价值。为此又产生了高次指数平滑。

（1）一次指数平滑法（Single Exponential Smoothing）。一次指数平滑法是另一种形式的加权移动平均，它不同于指数平滑法。加权移动平均法只考虑最近的n个实际数据，指数平滑法则考虑所有的历史数据，只不过近期实际数据的权重大，远期实际数据的权重小。一次指数平滑平均值SA_t的计算公式为：

SA_t=αA_t+（1-α）SA_t-1 （9-3）

若把t期以指数平滑平均值SA_t作为t=1期的一次指数平滑预测值SF_t+1，则一次指数平滑法的预测公式为：

SF_t+1=αA_t+（1-α）SA_t （9-4）(www.daowen.com)

式中，SF_t+1为t+1期一次指数平滑预测值；A_t为t期实际值；α为平滑系数，它表示赋予实际数据的权重，0≤α≤1。

式（9-4）可以改写成：

SF_t+1=SF_t+α（A_t-SF_t） （9-5）

式（9-4）是一个递推公式。它赋予A_t的权重为α，赋予SF_t的权重为1-α。将式（9-4）展开得：

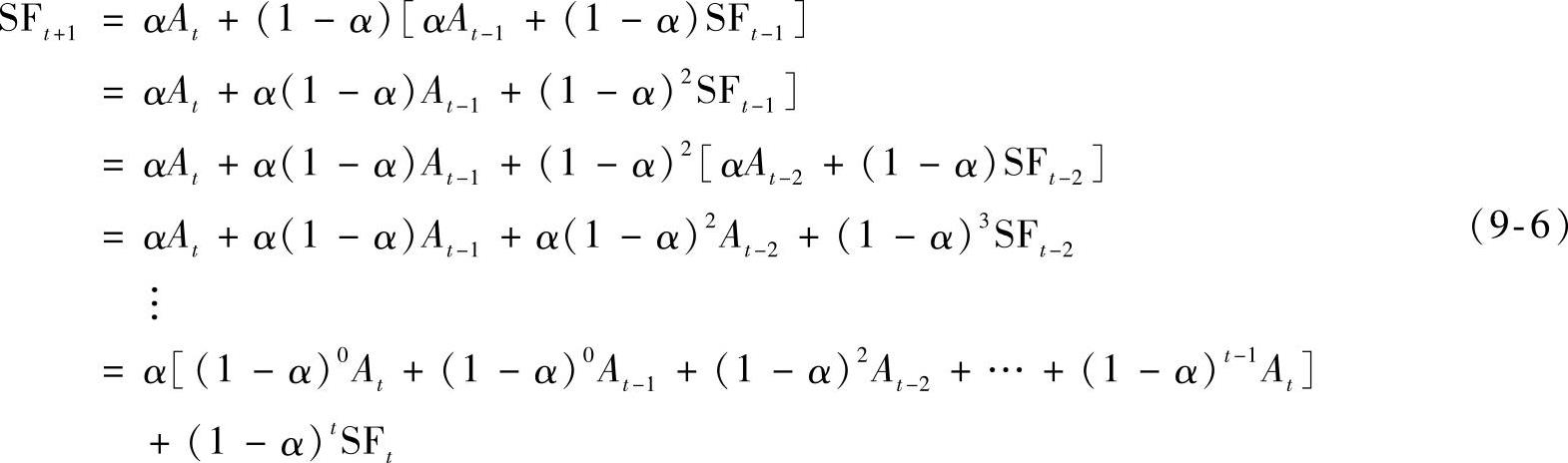
式中，SF_t=SA₀，它可以事先给定或令SF_t=A_t。

在式（9-6）中，当t很大时，（1-α）^tSF_t可以忽略。因此，第t+1期的预测值可以作为前t期实测值的指数形式的加权的和。随着实测值“年龄”的增大，其权数以指数形式递减。这正是指数平滑法名称的由来。

综上所述可知，预测值依赖于平滑系数α的选择。一般说来，α选得小一些，预测的稳定性就比较好；反之，则其响应性比较好。在有趋势的情况下，用一次指数平滑法预测，会出现滞后现象。面对有上升或下降趋势的序列时，就要采用二次指数平滑法（Double Exponential Smoot-hing）进行预测；对于出现趋势并有季节性波动的情况，则要用三次指数平滑法（TripleExpo-nential Smoothing）进行预测。

一次指数平滑法和移动平均法一样，只适用于具有水平趋势的时间序列。同时由于α与F_t-n的确定尚无较好的规则可循，也影响了方法的精度。特别当时间序列具有不断增大（或减小）的趋势时，用一次指数平滑法预测的结果往往出现明显的滞后现象，其误差较大。在这种情况下，需要用高次指数平滑法。

和移动平均法相比，指数平滑法有以下优点：

1）不需要储存过去较多时刻的历史数据。在时刻t预测t+1时刻的数值F_t+1时，只需知道t时刻的实际值x_t及预测值F_t即可。

2）对不同时刻的数据作了不等权的处理。

例9-3：表9-2中的数据是某股票在8个连续交易日的收盘价，试用一次指数平滑法预测第9个交易日的收盘价（初值S₀^（1）=y₁，α=0.4）。

表9-2 收盘价

（2）二次指数平滑法。二次指数平滑预测值可按下式计算：

F_t+p=SA_t+pT_t （9-7）式中，F_t+p为从t期计算，第p期的二次指数平滑预测值；T_t为t期平滑趋势值，T₀事先给定；SA_t为t期平滑平均值，又称为“基数”，SA₀事先给定。

SA_t可按下式计算：

SA_t=αA_t+（1-α）（SA_t-1+T_t-1）=αA_t+（1-α）F_t （9-8）

T_t可按下式计算：

T_t=β（SA_t-SA_t-1）+（1-β）T_t-1 （9-9）

式中，β为斜率偏差的平滑系数，其余符号意义同前。

通过二次指数平滑，再建立线性平滑模型可有效抑制滞后偏差，同时只有经过高次平滑才能实现跨期预测。

当时间序列具有抛物线趋势时，可以用平方指数平滑法进行预测。

此外，对起伏较大的序列，还可以用二次多项式来拟合，但需要进行三次指数平滑。在负荷预测中，一般平滑次数不宜超过三次。

指数平滑法在时间序列变化平缓时进行预测，才具有较高的精度，该方法主要是在短期及中期预测中得到了广泛应用。应当明确，因为事物发展的未来决非过去的简单重复，因此，时间序列预测法一般不适用于长期预测。

9.3.1.2 时间序列分解模型

实际需求值是趋势的、季节的、周期的或随机的等多种成分共同作用的结果。时间序列分解模型（Time Series Decomposition）试图从时间序列值中找出各种成分，并在对各种成分单独进行预测的基础上，综合处理各种成分的预测值，以得到最终的预测结果。

时间序列分解方法的应用基于如下假设：各种成分单独地作用于实际需求，而且过去和现在起作用的机制将持续到未来。因此，在应用该方法时要注意各种成分是否已经超过了其起作用的期限。同时，还应该分析过去出现的“转折点”情况。例如，1973年的石油危机对美国1973年以后的汽车销售纪录产生了重大影响。当用某种模型来预测今后十年的汽车销售量时，就应该考虑类似石油危机这样的重大事件是否会发生。

时间序列分解模型有两种形式：乘法模型（Multiplicative Model）和加法模型（Additive Mod-el）。其中，乘法模型比较通用。对于不同的预测问题，人们常常通过观察其时间序列值的分布来选择适当的时间序列分解模型。

图9-2给出了几种时间序列类型，在此以类型c为例，介绍时间序列分解模型的应用。线性趋势、相等的季节波动类型是线性趋势和季节变动趋势共同作用的结果。

用这种方法进行预测的关键在于求出线性趋势方程（直线方程）和解析数。

求解可以分以下三步进行：

（1）求趋势直线方程。首先根据表给出的数据绘出曲线图形，然后用简单移动平均法求出平均值，并将平均值标注在图上。为求趋势直线，可采用最小二乘法。

（2）估算季节系数（Seasonal Index，SI），即实际值与趋势值的比值的平均值。

（3）预测。再进行预测时，关键是选择正确的t值和季节系数。

在此需要指出的是，对线性趋势、相等的季节波动类型，可以用一种简明的比较方便的周期性预测方法。