1.从至表法

从至（From-to）表法是一种常用的生产和服务设施布局方法。利用从至表列出不同部门、机器或设施之间的相对位置，以对角线元素为基准计算各工作点之间的相对距离，从而找出整个单位或生产单元物料总运量最小的布局方案。这种方法比较适合于多品种、小批量生产的情况。

从至表法的基本步骤如下：

（1）选择典型零件，制定典型零件的工艺路线，确定所用机床设备。

（2）制定设备布局的初始方案，统计设备之间的移动距离。

（3）确定零件在设备之间的移动次数和单位运量成本。

（4）用实验法确定最满意的布局方案。

例8-1：某金属加工车间有六台设备，已知其生产的零件品种及加工路线，并据此给出如表8-3所示的零件在设备之间的每月移动次数，表8-4给出了单位距离运输成本。请用这些数据确定该车间的最佳布局方案。

表8-3 设备间平均移动次数矩阵（单位：次）

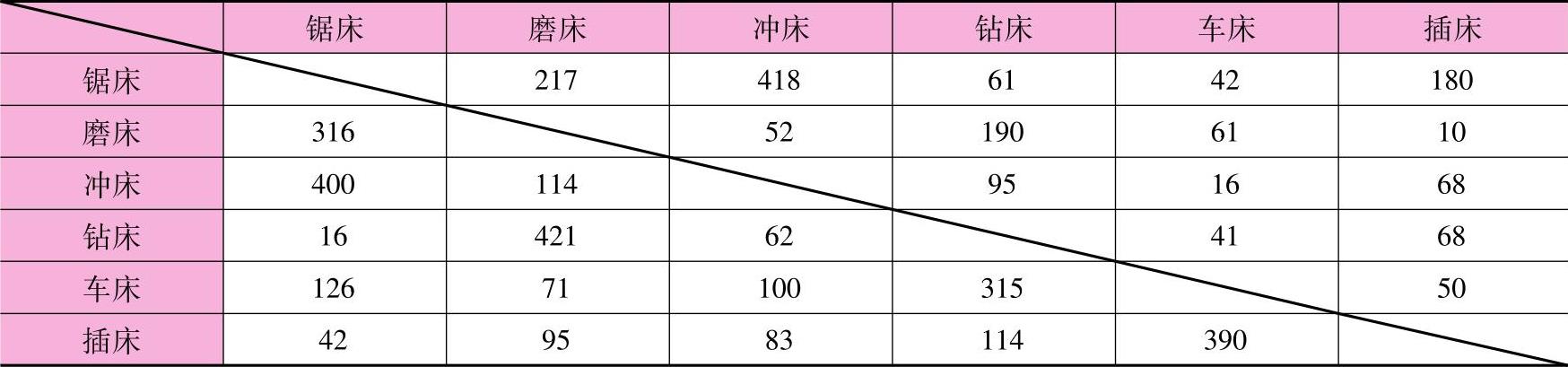
表8-4 单位距离运输成本矩阵（单位：元）

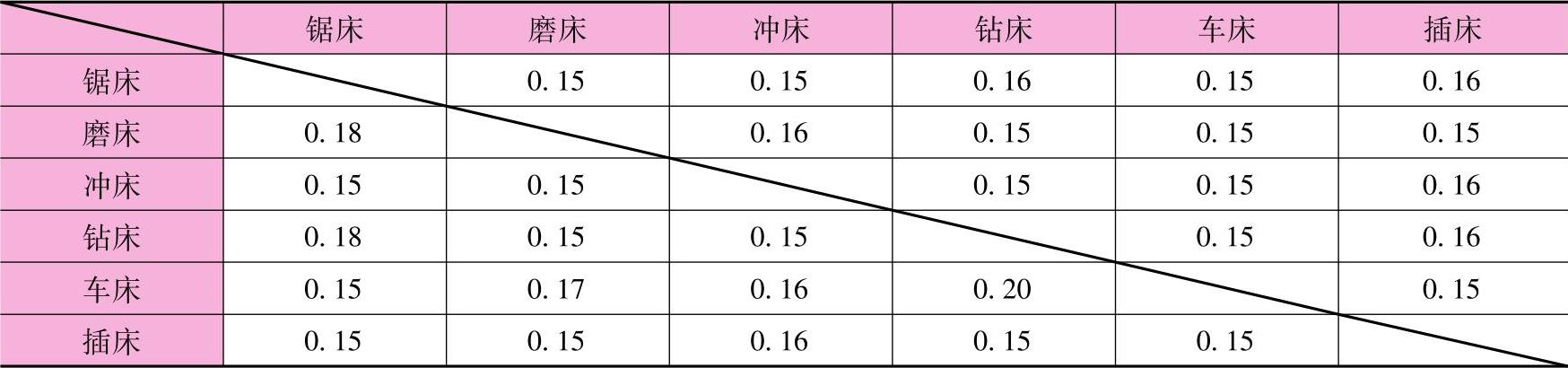
将运输次数矩阵与单位距离运输成本矩阵的相同位置的数据相乘，得到从一台机器到另一台机器的每月运输成本，如表8-5所示。然后，再将对角线对称的成本元素相加，得到两台机器间的每月总的运输成本，如表8-6所示。

表8-5 单位距离每月运输成本（单位：元）

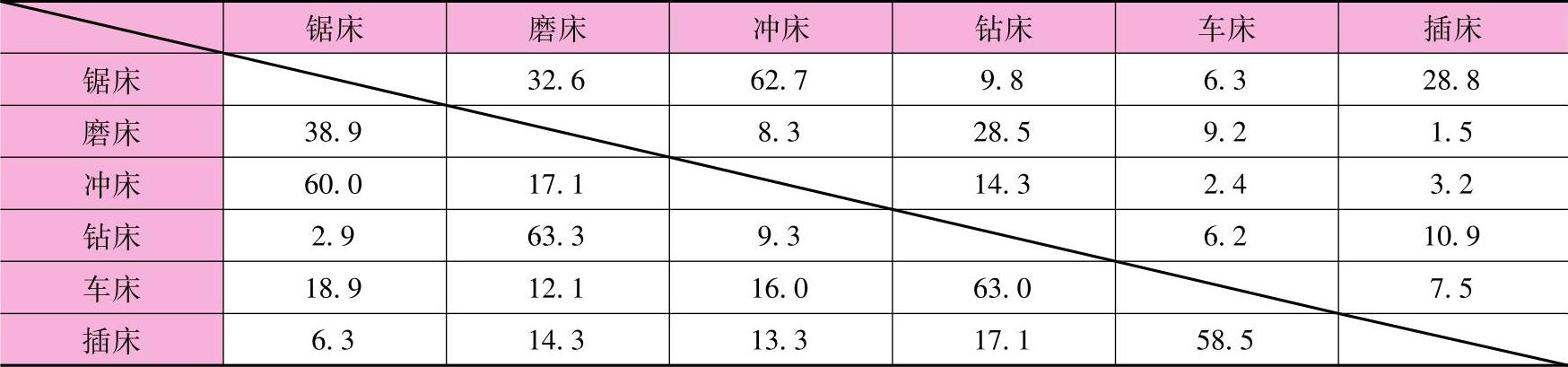
表8-6 单位距离每月总运输成本（单位：元）

确定紧密相邻的系数。其确定依据就是总运输成本的大小。按总运输成本的大小，从大到小降序排列，就得到了机器（或部门）之间的紧密相邻程度。本例中，根据表8-6中的①②③④⑤的顺序，应将锯床与冲床相邻布置，磨床与钻床相邻布置，锯床与磨床相邻布置，钻床与车床相邻布置，车床与插床相邻布置。最后结果如图8-9所示。

2.物料运量图法

从至表法的另一种应用是扩展成物料运量图法。

物料运量图法是按照生产过程中物料的流向及生产单元之间的运输量，布置企业的车间及各种设施的相对位置，其步骤为：

（1）根据原材料、在制品在生产过程中的流向，初步布置各个生产车间和生产服务单位的相对位置，绘出初步物流图。

（2）统计车间之间的物料流量，制定物料运量表，如表8-7所示。

图8-9 布局方案

表8-7 车间之间运量表（单位：t）

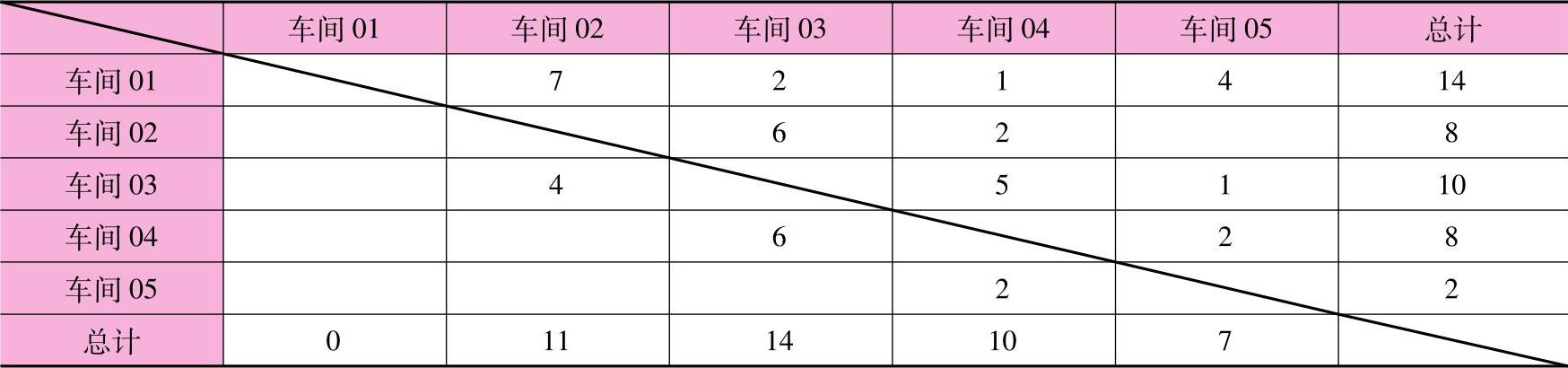
（3）按运量大小进行初试布置，将车间之间运输量大的安排在相邻位置，并考虑其他因素进行改进和调整。

最后的结果如图8-10所示。因为车间01和车间02、车间02和车间03、车间03和车间04之间的运量较大，所以应该相邻布置。

3.作业相关图法

作业相关图法由穆德提出。它是根据企业各个部门之间的活动关系密切程度布置其相互位置，据生产过程各单位的关系密切程度，确定各部门的相互位置的方法。

把相互间关系密切程度高的部门靠近布置。此法适用于运营过程中各部门间主要为非物流关系的情况。其步骤如下：

（1）确定部门关系级别。

（2）各部门联系程度识别。

（3）进行部门布置，把相互间关系最密切的单位靠近布置。

首先将密切程度划分为A、E、I、O、U、X六个等级，其意义如表8-8所示。然后列出导致不同程度关系的原因，如表8-9所示。使用这两个资料，将待布置的部门一一确定出相互关系，根据相互关系重要程度，按重要等级高的部门相邻布置的原则，安排出最合理的布置方案。

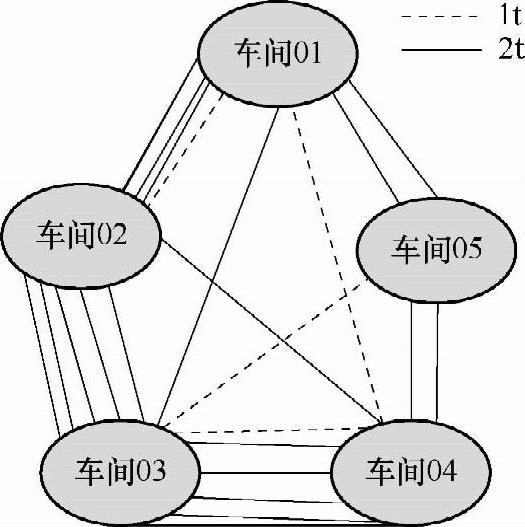
图8-10 运量图

表8-8 关系密切程度分类表

表8-9 关系密切原因

例8-2：一个快餐店欲布置其生产与服务设施。该快餐店共分成6个部门，计划布置在一个两排三列的区域内。已知这6个部门间的作业关系密切程度如图8-11所示，请作出合理布局。

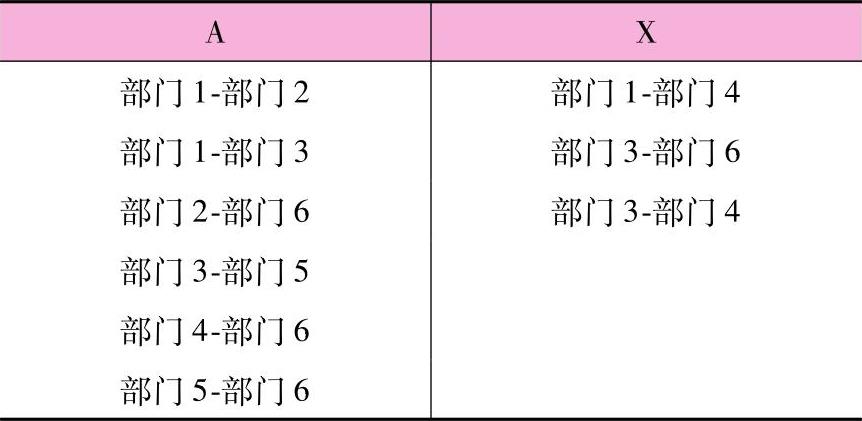
第一步，列出关系密切程度分类表如表8-10所示（只考虑A和X）。

图8-11 作业相关图示例

表8-10 关系密切程度分类表（只考虑A和X）

第二步，根据列表编制主联系簇，如图8-12所示。原则是，从关系“A”出现最多的部门开始，如本例的部门6出现3次，首先确定部门6，然后将与部门6关系密切程度为A的部门一一联系在一起。

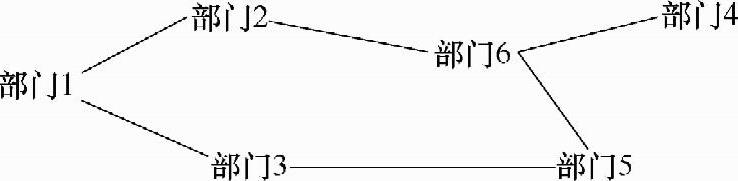
第三步，按次序选取A类的剩余部门，即考虑其他“A”关系部门，如果能加在主联系簇上就尽量加上去，否则画出分离的子联系簇。本例中，所有的部门都能加到主联系簇上去，如图8-13所示。

图8-12 联系簇

(www.daowen.com)

图8-13 修正后的联系簇

第四步，画出“X”关系联系图，如图8-14所示。

第五步，根据联系簇图和可供使用的区域，用实验法安置所有部门，如图8-15所示。

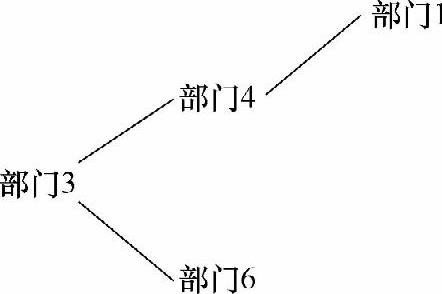
图8-14“X”关系联系图

图8-15 最后结果

4.新设备的布局问题

为适应生产或服务要求，常常对原有的部门进行改造。例如，在已有的设备设施中，再安置一台新装备。该问题的目标是使从新设备到老设备的加权直线移动距离的总和最小。为方便起见，假设物料或人员在两台设备或两个部门之间移动时，只能按交叉垂直的路线运动，即两个点之间不能走对角线。设原有设备在坐标内的点为（a₁，b₁），（a₂，b₂），…，（a_n，b_n），则目标是求出x和y，使得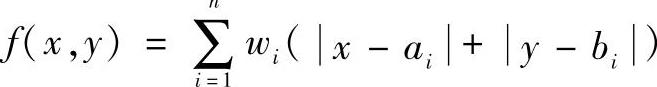最小。引进加权系数w是允许新、老设备间有不同的流量。

该问题的一个简化特点是可以分别求出x和y的最优值。即

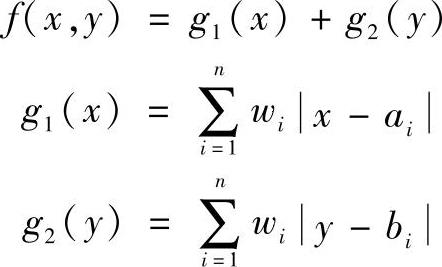
例8-3：假设有两台设备，分别坐落在（5，10）和（20，30）的位置，如图8-16所示。取权重为1。若x可取5和20之间的任何值，则g₁（x）等于15（例如，x=13，g₁（x）=|5-13|+|13-20|=15）。同样，若y可取10和30之间的任何值，则g₂（y）等于20。任何在[5，20]外的x和任何在[10，30]外的y，都将导致更大的g₁（x）和g₂（y）。因此，（x，y）的最优解应为5≤x≤20，10≤y≤30。落在图8-16的灰色框内的解都是最优的。从这个例子可以看出，x等于a_i的某个值、y等于b_i的某个值，该问题总存在最优解。

例8-4：某大学购买一台新设备，以便全校教师制作教学录像带。这台设备由校园内六个学院的教师使用。这六个学院的位置如图8-17所示。其坐标和各学院使用该设备的教师人数如表8-11所示。各学院间用草坪隔开，故通道都是交叉垂直的。该录像带制作设备安置在何处能使所有教师的总行程最小？

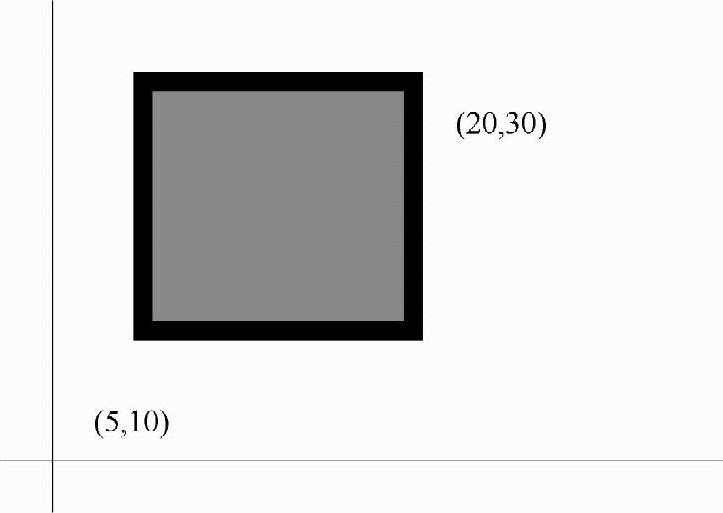
图8-16 新设备布局的最优区域

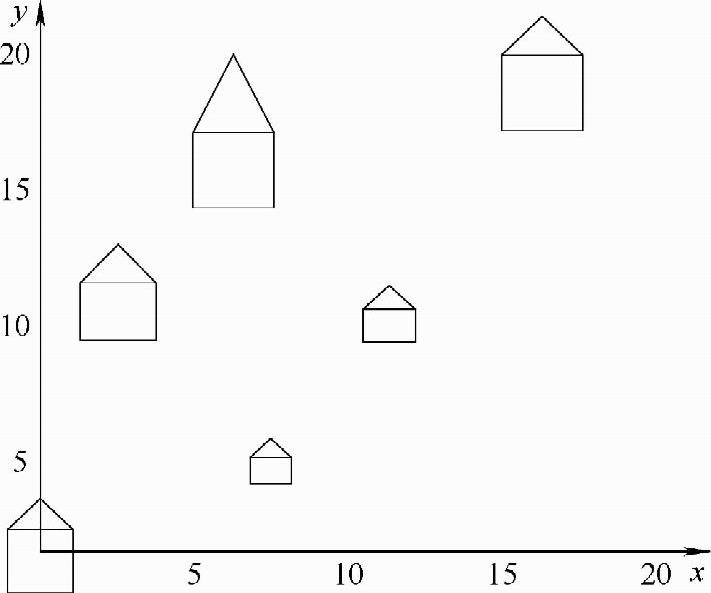
图8-17 学院坐标图

表8-11 学院坐标和使用人数

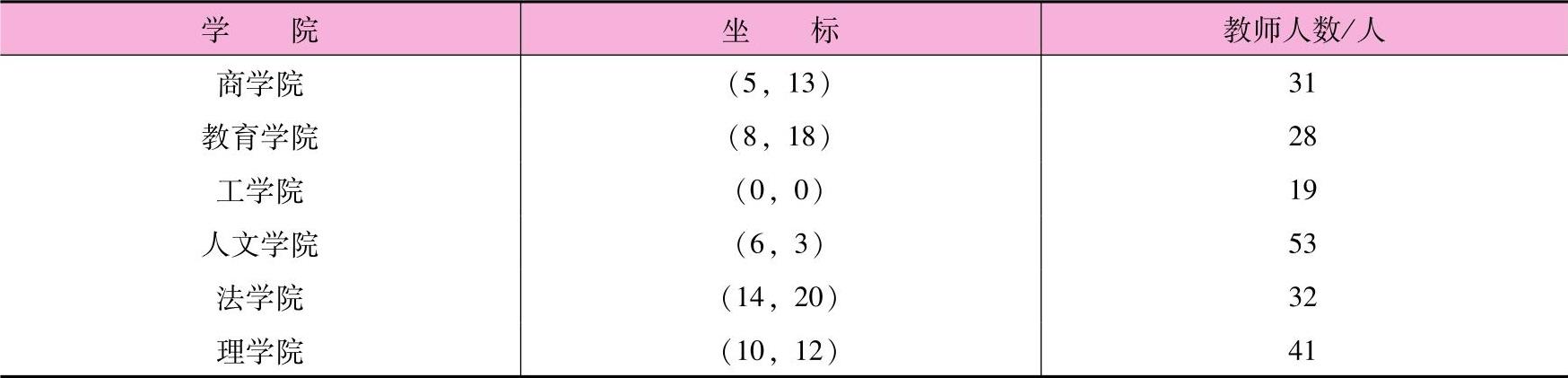
设布置录像带制作设备的坐标为x和y，取每个学院使用该设备的教师人数为加权数。下面分别求出x和y的值。

首先求x的最优解。将x的坐标按递增的顺序排列，同时求出累计加权值，如表8-12所示。

表8-12 x坐标和累计加权值

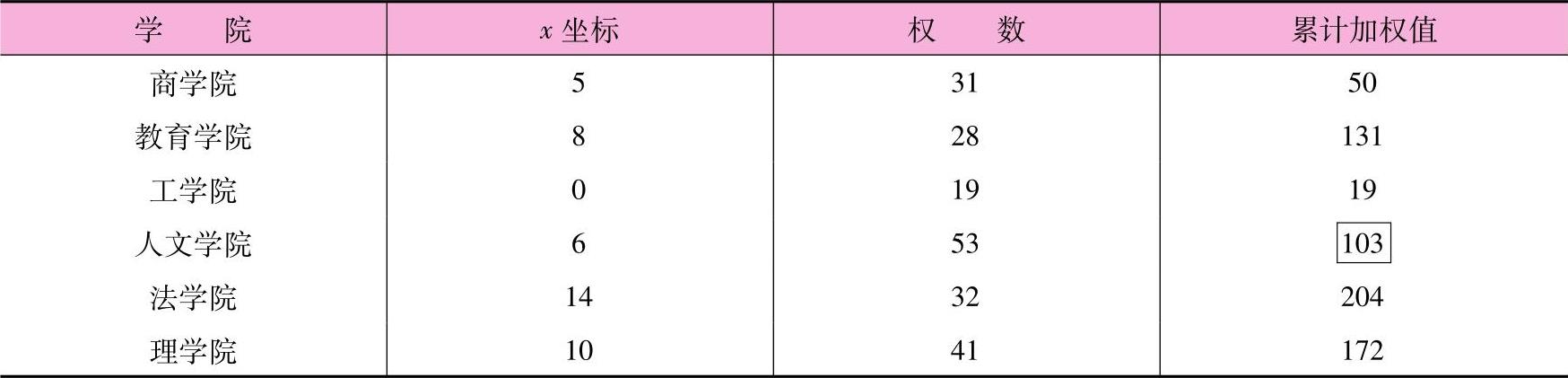
x最优值的求解方法：

（1）将累计加权值除以2，本例为102（204/2）。

（2）在累计加权值中从小到大找出第一个大于102的值，本例为103。

（3）与103相对应的x坐标即为最优解，即x=6。

y值的求法与此相同。由表8-13可知，y=12。则本例的最优解为（6，12），即新的录像带制作设备布置在坐标为（6，12）的地方，这样所有教师的行为路程的总和最小。

表8-13 y坐标和累计加权值

5.线性规划方法

一般来说，对于相对简单的问题可以用人工求解的方式。但现实中的问题往往涉及多个变量，此时求解是极为困难的。下面例子的优化目标是使总的物料搬运成本最低，是一个四重分配问题，不适宜人工方式求解。市场上有许多软件公司开发出来的优化软件包，如LINGO，就可以非常方便地解决这些问题。

设：n——机器数量。

c_ij——机器i布置在j时，单位时间的成本。

d_jr——从位置j到位置r物料移动一次的成本。

f_ik——单位时间内机器i到机器k的平均移动次数。

S_i——机器i可能布置的位置的集合。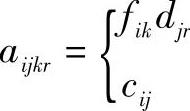 （如果i≠k或j≠r）{（如果i=k和j=r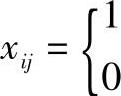） （如果机器i布置在位置j）{（其他）

a_ijkr——单位时间机器i布置在位置j和机器k布置在位置r的物料运输费用，这个费用仅在x_ij等于x_kr情况下出现。

因此，总成本表达式为：

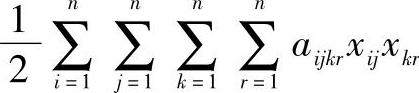
约束条件有：

该模型是一个线性规划问题，可以采用线性规划方法获得其最优解，而这个解即为最优的布局方案。

6.计算机辅助选址决策与设施布局

随着计算机在企业管理中的应用，越来越多的管理人员处理生产与服务设施布局时，通过计算机解决一些比较复杂的问题。计算机辅助设施布局设计（Computerized Relative Allocation of Facilities Technique，CRAFT）是一种常用的计算机辅助生产和服务设施布局的工具。

CRAFT的特点有：

（1）CRAFT采用启发式算法。其评价决策使用的规则是：每次互换两个车间的位置，如果布置的总成本降低了，则互换两个车间。

（2）CRAFT并不能确保得到最优方案。

（3）CRAFT严重依赖于初始状态，初始状态在一定程度上决定了最终的布局方案。

（4）CRAFT从一个合理的方案开始有可能产生一个成本更低的方案，但并不总是如此。因此使用CRAFT时最好提出几种不同的初始布局，以得到不同结果。

（5）CRAFT最多能解决具有40个车间的布局问题，迭代不到10次即能得到最终结果。

（6）CRAFT车间由标准方块组成，车间允许多种构形，但经常会得到奇形怪状的车间。为了得到一种理想布置，必须人为改变车间形状。