每一个排队问题的核心问题实际上就是对不同因素作权衡决策。管理者必须衡量为提供更快捷的服务（如更多的车道、额外的降落跑道、更多的收银台）而增加的成本和相应的等待造成的费用之间的关系。

通常，对于成本的权衡决策是十分直截了当的。例如，如果发现员工排队等候使用复印机所花费的时间能够用在其他的生产性活动上，就可以比较这种成本与增加一台复印机的成本。于是，这种决策就可转化为成本与收益的比较问题，这样会使决策变得直观和容易。

假如排队问题的核心是医院对病床的需求，则可以通过估算建设成本、所需新设备的费用和增加的维护人员成本，计算增加新病床的成本。但是有没有其他的衡量标准呢？这里面对的问题是要计算出一个病人到达医院而没有病床可用时，给医院带来的损失。我们可以估计出医院收入方面的损失，但是怎么估计由于医院能力不足而使得病人因得不到适当的救护而遭受的精神损失呢？

图6-5所表现的是在典型（稳态）的交通运输问题中基本的权衡关系。在开始的时候，服务能力最小，相应的等待成本也就最大。由于服务能力的增大，排队等待的顾客减少了，同时他们的等待时间也相应减少，所以等待成本也随之下降。可以通过负指数曲线来描述这一函数的变化情况。服务能力成本可以用简单的线性变化来表示，而不必用分段函数。复合成本或总成本则是一条U形曲线。对于这样的权衡问题，只是一般性的近似描述。理想的最优化（最小）成本位于服务能力成本曲线和排队等待成本曲线的交点上。

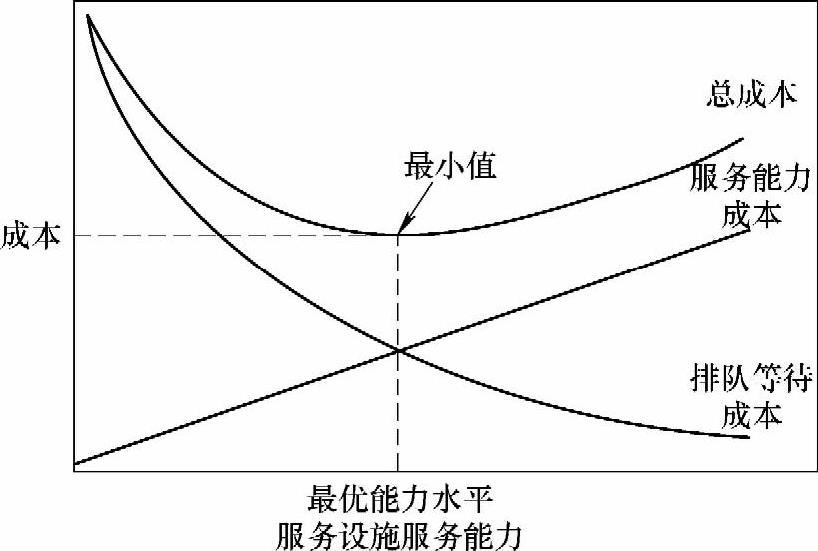
图6-5 服务能力和等待成本的权衡(www.daowen.com)

在开始对排队理论的技术性公式进行介绍之前，首先让我们直观地观察一下排队问题，这对我们了解其实际意义是非常有益的。图6-6表示的是到达某一服务设施（如银行）的人数和对于在这一设施中的服务的需求（如信贷人员的工作）。在服务系统提供服务的过程中，每小时到达系统的顾客人数是一个很重要的变量。从提供服务的观点来看，顾客对于服务的需求是不断变化的，而且经常超过服务系统所能提供的服务能力。我们可以通过一些不同的方法对到达人数加以控制。例如，只可允许很短的队长（如快餐店的驶入式服务口的空间很小），也可以为特定的顾客留出特定的时间段，或者提供特殊服务。对于服务期，可以通过使用更快或者更慢的服务人员、更快或者更慢的机器、不用的工具、不同的物料、不同的设施布置和更快的准备时间来影响服务时间。

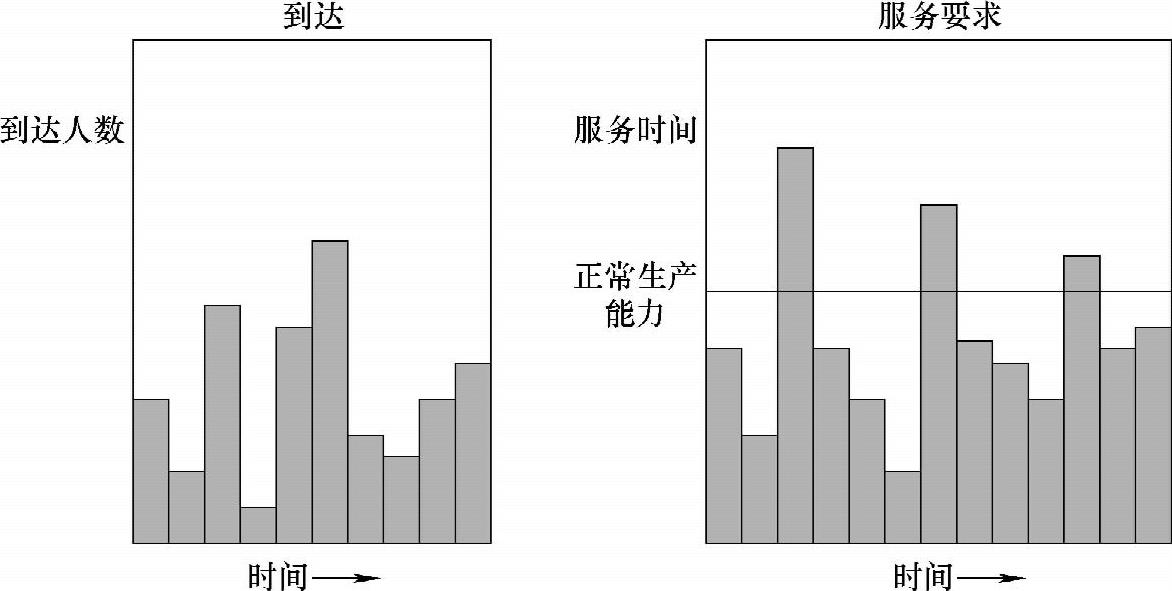
图6-6 顾客到达和服务分布图

从本质上来讲，排队问题并不是生产系统中的固定状态，它与系统设计和管理的控制有很大关系。理查德·拉尔森（Richard Larson）教授（著名的“等待观察家”）与他的同事们在对银行业多年研究的基础上提出了对排队问题进行管理的一些有益建议。