1. 新产品市场化模型

前文建立了单一经济人的生产和研发行为模型，本节将把模型扩展到多人并引入市场。在这里我们描述这样一个市场：一个小村庄有若干名自耕农生产产品X，过着自给自足的生活。其中一个自耕农获得产品Y的生产技术，他在满足自己对产品Y的需求之后，将可以向其他自耕农提供产品Y并换回产品X，此时我们称这个拥有了新技术的自耕农为“企业家”。下面，我们需要考虑这个市场上产品Y和产品X的交换比价。

假设1：只有企业家可以生产产品Y。

该假设排除了自耕农通过技术模仿获得生产产品Y的技术的可能性，同时企业家也不能雇用自耕农进行产品Y的生产。

假设2：自耕农是价格的接受者。

该假设排除了自耕农是强硬的讨价还价者（即使牺牲效用也要追求更有利的价格）的可能性。

假设3：该经济体中有1个企业家和n个自耕农。

在模型中，假设只有企业家具有生产产品Y的能力，从其他自耕农的角度看，消费产品Y可以获得很高的边际效用，如果可以减少一些产品X的消费或是多生产一些产品X用于交换产品Y将可以提高自己的总效用。自耕农想要购买多少产品Y将取决于产品的价格，也就是1单位产品Y需要多少产品X用于交换。

我们可以根据自耕农的效用函数求出单个自耕农对产品Y的需求曲线。

此时，自耕农的效用函数为：

其中，　XC表示自耕农生产的用于自己消费的产品X，YT表示通过交易用产品XT（为交易而生产的产品X）换回的产品Y，LXC表示自耕农为生产自己消费的产品X而投入的劳动，LXT表示为生产用于交易的产品　TX而投入的劳动。

令产品Y的价格PY为a，既1单位产品Y可以换的a单位产品X。

由于　　　　XC　=　LXC ，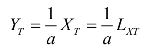

自耕农的效用函数可以转化为：

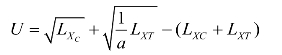
效用最大化时，由U对LXC、LXT求导并令导函数为0，可得：

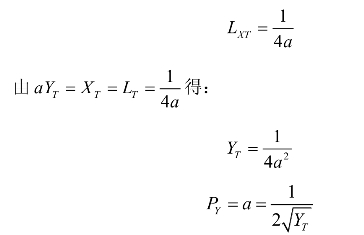
此函数即为自耕农对产品Y的需求函数，此时a的值应大于1/ 3，否则由于产品Y过于便宜，以至于自耕农愿意投入大量的劳动L以生产产品X用来与企业家交换产品Y而导致自耕农投入的劳动总量超出每年最大劳动投入量为1单位的限制条件。

从自耕农对产品Y的需求曲线不难看出，随着产品价格a的增加，自耕农对产品Y的需求量将不断下降，趋近于0。

首先，我们考虑只有一个自耕农的情形，企业家作为产品Y的唯一供给者，可以像垄断者那样定价。由于我们假设自耕农是价格的接受者，因此，在模型中不再考虑买方垄断的问题。由于企业家生产产品Y所投入的土地资源K相对充裕而没有经济成本，而投入的劳动L对总效用的边际影响是不变的，恒定为1，而根据效用函数中的假定，产品X的消费量较小的情况下，其边际收益是很高的，在产品X的消费量小于1 4时，其边际效用大于1；从企业家角度看，是在用边际效用成本固定为1的产品Y交换边际效用收益逐渐减少的产品X，因此，对于企业家来说，应该尽量充分利用垄断定价带来的优势，用产品Y换得更多的产品X。此时，企业家定价的行为类似于垄断市场上的垄断者，定价过低会导致用太多的产品Y换到较少的产品X，而企业家自己也能生产产品X，因此不用担心交换的产品X的数量不足的部分，定价过高意味自耕农因为不经济而不愿意交换足够的产品X，因此，一个类似利润最大化的求解方式能得到企业家的利润最大化定价。在这里，可以认为产品Y的边 际成本MC =PLT =1。

作为垄断者的企业家其收益函数为：

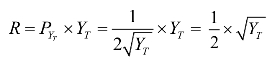
边际收益

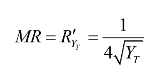
与常识相符，随着产品Y供给量的增加，其边际收益递减。当边际收益等于边际成本时，有：

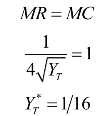
企业家效用最大化时的产品Y的市场供应量为=1 /16。企业家和自耕农的各项经济指标如表7-4所示。

表7-4　企业家和单个自耕农形成的市场均衡结果

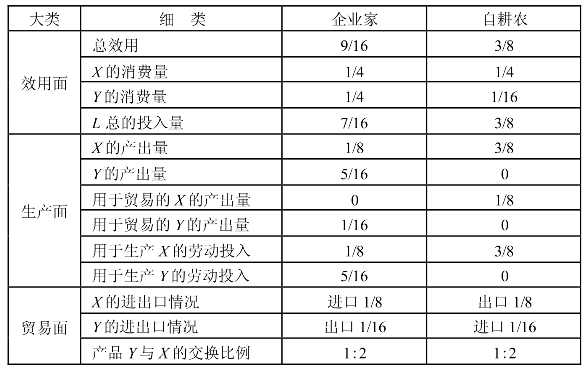
从表7-4可以看出，企业家出售产品Y比简单的自耕农技术选择模型中的自耕农自己生产X和Y自己消费时的1/2有所提高，企业家从贸易中获得好处，与不贸易的时候相比，企业家通过贸易节省了1/16单位的劳动投入。从自耕农的角度看，与自耕农型经济人模型中自耕农只生产产品X时相比，自耕农的总效用有所提升，由不贸易时的1/4提高到贸易后的3/8，自耕农用增加1/2单位劳动的代价换得了1/16单位的产品Y。正如亚当·斯密的理论所阐述，贸易对自愿参与的双方都有好处。

单个自耕农对产品Y的需求曲线为：

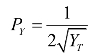
那么，n个自耕农的需求加总形成的市场需求为：

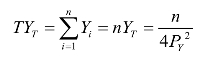
式中，　TYT表示市场对产品Y的总需求，YT表示单个自耕农对产品Y的需求，此时两者不再相等。

市场需求曲线为：

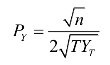
在新的市场需求曲线下，企业家对产品Y的定价以及产量决策将随着n的变化而发生变化。在本模型的假定情况下，企业家的决策可以分为三个阶段。

第一阶段：在一个自耕农的情形下，企业家通过自己生产产品X作为贸易获得的产品X的补充，类似于在患者较少的乡村，乡村医生同时也自己种地时的情况。而在我们通常的印象中，企业应该是专业化生产的，也就是专业化地进行产品Y的生产，类似于城市里医院的情况，医生们可以完全依靠行医的收入作为收入的核心来源。显然，在我们的模型中，随着自耕农数量的增多，企业家也将会通过贸易获得更多的产品X，从而实现专业化生产。

表7-5　两个自耕农时的企业家和典型自耕农的市场均衡结果

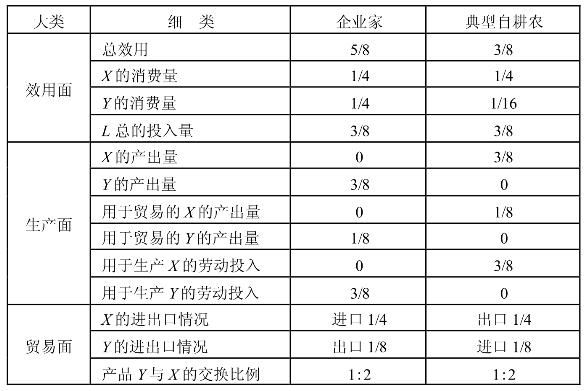
如表7-5所示，在我们的模型参数的设定条件下，两个自耕农时，企业家正好实现专业化生产。与一个自耕农时的计算方法相同，可以求得两个自耕农时，企业家和自耕农在市场均衡时的经济指标。相比一个自耕农时的情况，企业家生产了更多的产品Y，同时不再生产产品X。此时，价格不变，而自耕农的效用和生产，交易情况和之前一个自耕农时一样。

值得特别注意的是，此时产品X带来的边际效用

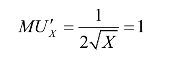
需要考虑这样一种情况，随着产品X的消费量逐渐提高，其边际效用逐渐下降，可能会低于企业家投入劳动生产产品Y的负的边际效用，在本书中将其称为边际效用成本。在这种情况下，企业家在为产品Y定价时，最大量的获得产品X未必能实现企业家的利润最大化，当产品X带来的边际效用收益小于生产产品Y的边际效用成本时，企业家会提高价格，用更多的产品X的量来对其降低了边际效用作出弥补。

第二阶段，在我们的模型中，当第三个自耕农进入市场时，企业家已经实现了专业化生产，同时产品X的边际效用已经与劳动投入的边际效用成本相等，此时，企业家将会调整产品Y的价格，以保证效用最大化。

此时企业家的效用函数为：

由于此时实现了专业化生产，企业家的所有的产品X均来自市场，有　X =PY×TYT ；此时，企业家消费的产品Y仍将保持自给自足，因此仍为1/4；企业家的劳动投入量L=LT+LC ；其中，LT为生产用于贸易的产品Y投入的劳动，LC为生产企业家自己消费的产品Y。此时效用函数可以化为：

因为市场需求曲线为：

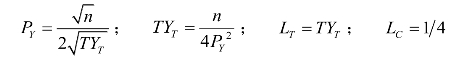
此时：

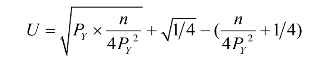
可以求出当U最大化时，企业家的定价

基于定价，我们可以计算出随着自耕农数量变化，企业家和自耕农的经济指标的变化。

表7-6反映了自耕农数量从2增加到16时企业家和自耕农的部分经济指标的变化情况。

表7-6　多个自耕农时的企业家和典型自耕农的市场均衡结果

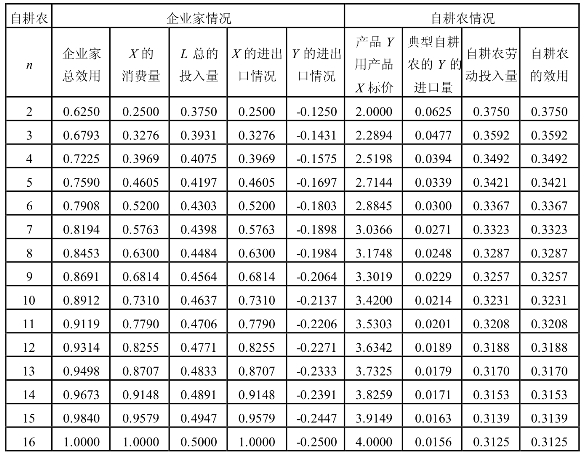
从表7-6中可以看出，产品Y的价格不断增加，企业家的效用不断提高，典型自耕农的效用则越来越低。显然，在垄断市场上，市场规模越大，越有利于企业家而不利于单个的自耕农。

第三阶段，随着自耕农的数量不断增加，一方面企业家不断地提高产品Y的价格，另一方面产品Y的供给量也在缓慢地增长，一个比较重要的节点是当企业家把产品Y的产量增加到1的时候，由于我们的模型假设企业家只有1单位的土地资源和劳动力用于生产，且不能通过租赁土地和雇用其他自耕农的方式扩大生产规模，因此，企业家生产产品Y的产量上限为1。在我们的模型中，当第432个自耕农进入市场时，产品Y的产量首次达到1，之后，随着自耕农的进一步增加，再想扩大产品Y的市场供给就只能减少企业家自己的产品Y的消费量。显然，此时对企业家来说产品X的边际效用远远低于产品Y的边际效用，并且随着增加产品X的消费，产品X的边际效用将继续减少，同时减少产品Y的消费还会进一步增加产品Y的边际效用。因此，在这个节点之后，企业家提高产品价格的速度会加快，随着产品市场上产品Y的供给无限趋近于1，产品Y的价格将趋近于正无穷。

和前两个阶段的情况不同，当企业家生产的产品Y产量达到1时，企业家的需求函数为：

由于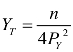，在企业家效用最大化的约束下，可以求出价格与自耕农数量的关系：

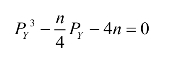
根据一元三次方程的求根公式，可以得到该方程的解：

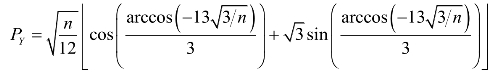
从上式可以看出，当n趋于无穷大时，产品Y的价格PY趋于无穷，产量YT趋于1。

图7-3

由图7-3可以看出，随着产品Y的均衡供给量的增加，产品Y的价格变化可以划分为三个阶段：

第一阶段，企业家不断专业化，产品X生产得越来越少，产品Y生产得越来越多，直到完全专业化。在这个阶段，企业家通过交换获得的产品X边际效用虽然也递减，但仍然高于为生产产品Y而投入的劳动带来的边际效用成本，企业家愿意最大限度地获得产品X，因此在定价的时候像典型的垄断厂商那样希望用尽可能少的产品Y获得最大量的产品X。

第二阶段，产品Y的产量扩大，价格缓慢上升，价格不断提高。同时，企业家生产越来越多的Y直到不得不减少自己的产品Y的消费。在第二阶段，企业家消费产品X的边际效用已经低于生产产品Y所要投入的边际效用成本。此时，需要更高的价格才能弥补产品X和产品Y之间的效用差。

第三阶段，产品Y产量缓慢增长，价格急剧上升。在这一阶段，企业家已经投入了所有的劳动用于生产Y，继续增加产品Y的销售需要减少自己消费产品Y的数量。此时，企业家的定价需要考虑由于减少产品Y的消费而导致的效用损失。(www.daowen.com)

2. 企业家的产量扩张模型

在新产品市场化模型中，我们考察了不同市场规模对市场均衡结果的影响，同时假定了企业家不能通过租用土地和劳动力的方式扩大生产规模，从而限制了产品Y生产规模的扩张。在本模型中，我们考虑放松这一假定的情况，即当企业家可以通过租用土地和雇用劳动扩大生产规模时，市场均衡结果会发生怎样的变化。

假设1：在我们的模型世界中，只有企业家和自耕农两种经济主体。现在要引入兼并，我们可以把兼并理解为企业家通过租用自耕农的土地和劳动力扩大产品Y的生产。此时，被企业家雇用的自耕农成为了一种新的职业，即自带土地的工人，同时我们假设成为工人的自耕农不再生产产品X，企业家把产品X作为工资支付给工人，工人虽然在企业家的管理下生产产品Y，但也需要在市场上用产品X来购买产品Y。这样，由于将工人引入了模型，也就将要素市场引入了模型。在要素市场上，企业家是工人劳动（和土地资源）的购买者。

假设2：考虑到交易成本和企业家管理能力的限制，我们假设企业家每期只能雇用一个自耕农成为工人。

假设3：自耕农的总数不变，保持为n。该假设意味着企业家增加工人将导致生产产品X的自耕农的减少。在产品Y的价格水平不变的情况下，将减少企业家通过交换获得产品X的总量。

由于在本模型中，工人和自耕农在能力方面没有任何差别，因此，工人实现的个人效用应该和自耕农相同。因为，如果工人的收入太低以至于效用低于自耕农，那么没有人会接受企业家提供的工作。反之，如果工人实现的效用高于自耕农，那么其他的自耕农将愿意接受更低的工资来提供同样的劳动力。

因此，可以通过自耕农和工人的均衡效用相等来计算工人的工资水平。自耕农的效用函数为：

其中　AU表示自耕农的效用，XA表示自耕农消费的产品X，YA表示自耕农消费的产品Y，LA表示自耕农投入的劳动总量。与之前的模型相似，XA =1/ 4，PY×YA=LA -1 /4。

此时，

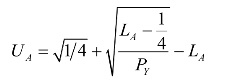
效用最大化时，即　U′AL =0时，

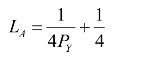
可得：

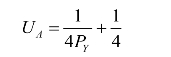
此时，工人的效用函数为：

其中UC表示工人的效用，XC表示工人消费的产品X，YC表示工人消费的产品Y，LC表示工人投入的劳动总量。由于工人通过劳动换取产品X作为工资，之后再用工资的一部分在市场购买产品Y，因此总收入等于总消费。

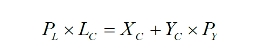
可得：

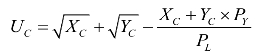
当工人效用最大化时，可以用Uc对　XC和,Y求导数，得：

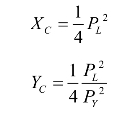
效用函数可以化为：

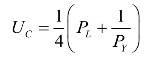
由于自耕农和工人的效用相等，可得：

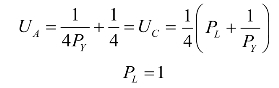
根据推导，可知企业家在为劳动定价时，可以按照1单位劳动支付1单位产品X的工资水平定价。由于一个自耕农生产产品X的生产函数也是1单位劳动生产1单位产品X，因此，对于一个自耕农来说，自己生产产品X在市场上交换Y和作为工人为企业家生产产品Y并获得工资是无差异的。

此时

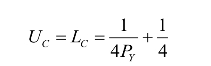
工人会投入的劳动量取决于产品Y的市场价格。价格越高，工人愿意投入的劳动量越少。

当企业家可以用　PL=1的工资水平来雇用工人扩大生产时，用一单位产品X的成本雇用工人生产LC单位的产品Y，显然，出售这些产品Y可以获得远超出作为工资成本的产品X的数量，对企业家来说，雇用生产是有利可图的。

当考虑企业家的雇用行为时，企业家面对的市场规模是一个很重要的影响因素。根据新产品市场化模型中的情形，随着市场规模的扩大，企业家逐渐实现了专业化，当企业家的产能达到极限后，价格将快速上升。在三个不同阶段企业家有不同的定价方式，因此有必要分别考察企业家在不同市场规模下的雇用决策。

在市场规模较小的时候，对应模型中n从1～2的阶段。此时，企业家在向市场提供产品Y的同时，也自己生产产品X，尚未实现生产的专业化。按照模型的假设，企业家可以在要素市场上雇用唯一的自耕农生产产品Y支付产品X作为工资，同时在产品市场上以相对高的价格像工人出售产品Y回收部分产品X。然而，由于工人可以选择不接受企业家的雇用，所以企业家为工人提供的总效用不可能低于自耕农时的水平。然而，自耕农转变为工人虽然增加了产品Y的供给，但是也减少了产品X的生产，因此这样做可能并不能提高企业家的总效用。

当市场规模较大的时候，对应模型中n从2～432的阶段，此时企业家实现了专业化生产，产品Y的市场价格较高。企业家通过雇用工人，适当降低产品Y的价格，增加产品Y的销售量，可以实现效用的增加。

与之前的情况不同，当企业家生产的产品Y产量达到1时，企业家的效用函数为：

其中X =PY×YT -mPL×LC ，企业家消费的产品X等于销售产品Y获得的收入PY×YT 与支付给工人的工资的差额，考虑雇用m个工人的情况，　mPL ×LC 表示工人的总工资，其中PL=1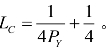；Y =　YBC +mYC-YT ；企业家自己生产的产品YBC加上工人生产的产品 mYC是产品Y的总产量，减去在市场上出售的产品YT就是企业家消费的产品Y的量。企业家此时只生产产品Y，随着雇用工人的数量增加，企业家自己生产的产品Y 将越来越少。企业家的效用函数可以化为：

式中的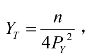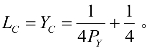效用函数可以化为：

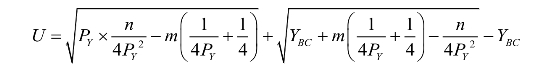
此时，令U对YBC求导等于可以求得效用最大化时

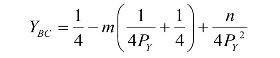
效用函数进一步化为：

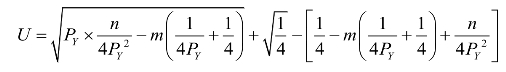
这时得到了产品Y的定价和企业家效用的关系。令U对Py求导等于0，理论上可以得到一个n和m作为参数的一元三次方程。通过解方程，可以得到用n和m表示的Py。

由于计算比较复杂，在这里我们只对企业家雇用工人的情况进行定性的讨论。如果市场规模很大，企业家已经投入了所有的劳动力，产品Y的产能达到了极限，也就是市场化模型的第三阶段，此时，从消费产 品X、产品Y和劳动的边际效用情况看有：

MU　X ＜MUL　＜MUY 　=　MUY×PY

当企业家获得了更多的产品Y时，首先企业家将按比例地增加产品Y的消费和出售，使增加的产品X和产品Y的消费带来的效用增加相等。这个过程持续到产品Y的消费增加到1/4时。此时，进一步增加工人对产品Y的生产，将允许企业家减少劳动投入。在这个过程中，企业家不会增加产品Y的消费，直到企业家自己的劳动投入下降到0。之后，进一步增加工人对产品Y的生产，企业家将再次在保持产品X和产品Y消费的效用增量相等的条件下，同时增加产品Y的消费和出售，这个过程持续到产品市场上的边际效用收益等于边际效用成本，作为一个垄断厂商，产品市场上产品Y的均衡价格将高于边际效用成本。

从消费者的角度看，随着产品Y的生产规模扩大，消费者可以用更低的价格购买到更多产品Y，产业的扩张是一个有利于消费者的过程。

在前面的模型中，我们假定自耕农直接获得了产品Y的新技术。产品Y相对于产品X来说是一种全新的产品，增加产品Y的消费并不会影响消费者消费产品X获得的效用。然而，这只是新技术诸多可能情形中的一种。根据熊彼特对技术创新的定义，新技术可能对应多种情况。熊彼特划分了创新的五种类型。借鉴熊彼特的创新分类，从生产函数的形式出发，可以将技术创新分成三类。一个典型的生产函数包括三个要素，即投入、产出、生产工艺。而这三个要素的变化都可以实现利润的增加，下面我们就分别讨论三类技术创新。

第一类技术创新，通过增加有效产出实现技术创新。这里所强调的增加有效产出特指在生产函数的投入和产品都不发生明显变化的情况下，通过减少无效的劳动和资源的浪费来提高生产效率，增加有效产出。如同亚当·斯密在制针工厂的案例中所描述的，一个工人专门从事一项工作，就可以减少在多项工作间频繁转换造成的时间浪费。即使扣针的投入品和扣针本身的质量都无明显变化，只是通过减少了不必要的损失就提高了生产率。从生产函数的角度看，投入的人力、工具和材料都没有发生变化，产出的扣针质量没有明显变化，但扣针的产量却得到了大幅度的提升。这种变化将通过函数形式的变化体现出来。

改进工具比通过分工提高效率的情况更为复杂，当新的生产工具引入生产过程时，必然伴随着投入品的变化。如果新生产工具的引进不显著增加生产成本，如工人自制了手工工具用于辅助生产，那么改进工具和分工在提高生产率的效果方面作用是接近的。但如果新工具本身成本很高，如将蒸汽机引进纺织作坊，那么，这种情况将更接近第二类技术创新。事实上，不同类型的技术创新之间并没用绝对的界限。在一项技术创新中，一般情况下，生产工艺、投入和产出会同时发生变化，只是有些变化对经济上的成本和收益没有显著影响，因而可以忽略。

第一类技术创新可以用如下两个生产函数表示：

原生产函数：　　　　X1=F1（K，L1）

新生产函数：　　　　X2=F2（K，L2）

第二类技术创新，通过引入廉价要素实现技术创新。在不改变产品质量的情况下，能够用充足廉价的生产要素代替昂贵稀缺的生产要素，可以实现利润的显著提升，一个典型的例子是胶合板代替实木板材生产门，用实木板材制作门成本相对高昂，而将胶合板替代实木板没有明显的改变门的质量，但是有效地降低了生产成本。

原生产函数：　　　　X=F（K1，L）

新生产函数：　　　　X=F（K2，L）

生产工具的重大变化也体现为廉价要素的引入和替换。如上文提到的将蒸汽机引入纺织作坊代替手工织机的情况，投入的资本要素发生显著的变化。通过蒸汽动力代替人力可以提高生产效率，生产更多的产品，从而降低单位成本。为了强调设备的重要性，我们可以在生产函数中用E表示设备。

原生产函数：　　　　X=F（K，E1，L1）

新生产函数：　　　　X=F（K，E2，L2）

第三类技术创新，通过提高产品质量实现技术创新。当新产品的产品质量发生变化时，如可以实现一些新功能、获得一些新属性，可以帮助消费者实现更高程度的效用。需要特别注意的问题是新产品和旧产品之间的替代性如何，或者说新产品和旧产品之间的差异有多大。实际上，可以根据新产品和旧产品的替代性大小不同来区别根本性创新和渐进性创新。

如果新产品和旧产品的差异足够小，那么新产品和旧产品间将接近于完全替代。两种产品将像同一种产品的情形一样，存在着统一的边际效用递减的情况。例如两个品种的苹果如果差别不大，那么消费者在吃了一个苹果之后再吃第二个就会产生边际效用递减的结果。而如果这两种苹果差别足够大，那么消费两种苹果带来的效用就应该是独立的。类似在自耕农模型中，如果产品Y和产品X的差异足够大，引入产品Y后的效用函数为：

与根本性创新不同，如果新产品和旧产品具有较强的替代性，则效 用函数的形式应为：

当一个消费者可以同时消费两种不同质量的产品，而这两种产品存在着较强的替代性时，那么消费这两种产品的次序就将影响到总效用。从理论上看，先消费高质量产品，后消费低质量产品是有利于实现效用最大化的。因此，能用高质量产品就先用高质量产品。当高质量产品问世时，消费者会优先购买高质量产品，而且由于消费者优先消费高质量产品，因此，高质量产品带来的边际效用也高，为了获得高质量产品，消费者愿意付出更高的代价，从而使高质量的产品比低质量产品价格高很多。

假设产品Y2的质量比产品Y1高一倍，也就是在消费相同数量的情况下，产品Y2带来的效用比产品Y1高一倍。那么，如果一个消费者要消费产品Y1和Y2各一单位，那么消费者将先消费产品Y2。如图7-4所示，消费者的总效用为：

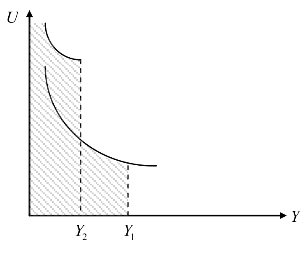
图7-4

因此，在理论假设条件的基础上，可以认为，一旦通过渐进性创新获得了高质量产品的生产能力，那么高质量产品将会在市场上代替低质量品，这也将成为企业家进行渐进性创新研发投入的原动力。

在根本性创新和渐进性创新之外，还应该关注模仿性创新的情况。有时候人们认为模仿性创新类似“山寨”根本算不上技术创新。然而模仿确实能使一个经济人获得新技术，并且在历史上和现实中，通过这种方式实现的技术进步，可能比知识产权交易、直接投资等典型意义上的技术扩散更加源远流长和普遍存在。因此，模仿性创新也应该得到重视。

模仿性创新与渐进性创新不同，渐进性创新的前提条件是已经掌握了一种产品的生产技术，要在已有的生产技术的基础上进行升级和完善。模仿性创新则不具备相应的技术基础。同时，模仿性创新也与根本性创新不同，根本性创新没有成功的案例可以借鉴，而模仿性创新允许对成功的根本性创新进行观察，从而降低研发失败的风险。舒尔茨在《改造传统农业》中指出，新技术的扩散速度主要由潜在收益决定。本书认为更重要的是要重视“等待”的作用，“等待”而不是立刻开始投资于“研发”可以更多地对其他企业进行观察，收集更多的信息，从而降低研发的风险。Everrett M. Rogers在《创新扩散》（Diffusion of Innovations）中指出，美国农民在采用一项新的农业技术时会经历认识、说服、决定、实施、证实五个阶段。通过各种不同渠道获得技术的相关信息在模仿创新过程中非常重要。观察可以降低研发失败的风险，但要获取新技术最终还是要付诸实践的检验，而这个实践检验的过程也就是模仿创新中的研发过程，我们可以称这个过程为模仿。那么，模仿性创新可以分成观察和模仿两个阶段。模仿性创新要进行的研发也仍然存在着不确定性和研发成本，一般来说，模仿性创新的研发成本会远低于根本性创新的研发成本。