1. 自耕农型经济人模型

我们假设一个经济人在自己拥有的土地上耕作，自给自足，从而可以建立一个最简单的模型作为分析起点。

资源集：K=1，L=1

该经济人拥有1单位土地，土地用K表示，该经济人每年都可以重复利用这1单位的土地，同时，该经济人每年拥有可支配的1单位劳动力用L表示。

生产函数：X=F（K，L）

该经济人拥有生产产品X的能力，生产1单位X需要消耗1单位劳动L和1单位土地K，L和K的投入量可以不是整数，只需要保持固定比例K、L投入，比例为1:1，该假设条件默示的保证了该经济人使用的生产技术固定。

效用函数：

在本模型中，经济人的效用取决于消费的产品X和投入的劳动L，其中消费商品X给该经济人带来边际递减的正效用。投入劳动L会给经济人带来负效用，相对于劳动，经济人更愿意享受无拘无束的自由时间。其中，劳动L的边际效用为1，这样假设的主要出发点是为了简化计算，同时，这样的假设也存在一定的合理性，因为人们在疲劳之前的工作中，劳动带来的负效用可能并不明显。

在这个模型中，经济人为了实现效用最大化，可以对产品X的产量进行选择。显然，要生产更多的产品X就需要投入更多的劳动L。由于劳动L和产品X之间存在着1:1的固定比例，因此，效用函数可以写为：

即经济人可以选择一个能使效用最大化的劳动量L。通过U对L求导，并令其为零时，可以得到U的最大值，此时劳动投入L即为均衡的劳动投入L*，L*的取值为1/ 4，最大化的均衡效用U*的值为1/ 4。

从均衡结果不难发现，经济人的理性选择并不是简单地追求产出X的最大化。我们在现实经济中也可以找到类似的情况。在人口稀少的农村，农民们也并不是不顾劳累地开垦所有的荒地，而是宁可更多地休息而允许一些土地处于自然的状态。

上述自耕农经济人模型是简单一般均衡分析的基础，也是最简单的经济人模型，本章的余下部分将其称为自耕农模型，将这样的经济人称为自耕农。

2. 简单的自耕农技术选择模型

自耕农技术选择模型指将一种新的生产技术（生产产品的技术）引入自耕农模型后形成的新的经济条件下的模型。自耕农按照固定的技术生产固定的产量，是一种静态的均衡。而现实经济中，类似自耕农的经济主体会有一些机会应用新技术，也就是采用新的生产函数。当自耕农获得了一种新技术时，将可以在两种技术中进行选择。

在本模型（自耕农技术选择模型）中，我们考虑这样一种情况，即自耕农获得了一种生产新产品Y的技术，那么此时自耕农的均衡生产行为会发生怎样的变化呢？（理论上，技术创新可以有多种不同的类型，生产一种新产品只是技术创新中的一种情况。）

首先，假设一个典型的自耕农获得了生产Y（比如生产棉花并制作衣服）的技术，其生产函数为：

其中，按照固定比例，一单位K和一单位L可以生产一单位Y。在这个假设条件下，K依然表示土地；Ly则表示生产Y所需要的劳动，Ly的下标表示生产产品Y所需的劳动和生产X所需要的劳动在技术上存在着差异。同时，生产单位产品Y所需投入的资本K和劳动Ly的劳动时间仍然是相同的。在现实经济中，随着生产规模的扩大，一些新的生产技术会被应用于生产过程，从而导致产品的边际成本递减。在本假设条件下，生产技术是被固定的，资源的质量也是同质的，因此也不存在生产规模扩大而不得不使用较差的资源导致的边际成本上升的情况。

再假设自耕农消费产品Y的效用函数与产品X相似，将产品Y引入自耕农的效用函数，则新的效用函数为：

效用函数：

在这个效用函数中，Y的消费量对消费X给经济人带来的效用是没有任何影响的，也就是说，包含着这样的假定：产品X和产品Y既无互补性又无替代性；综合产品Y的生产函数和效用函数的假设条件，意味着经济人对产品X和产品Y的需求偏好是相同的，并且生产产品X和产品Y的经济成本是完全相同的。如果调整假设使Y产品消耗更少的资源或带来更大的效用，那么，经济人将考虑优先生产产品Y。但是，由于边际效用递减的假定，产品X也会被生产，但均衡产量将小于产品Y的均衡产量。

显然，消费X产品和Y产品给自耕农带来的效用是相同的，生产成本也相同，因此自耕农根据效用最大化原则，两种产品的均衡产量应该是相同的。与自耕农模型算法相似，在本模型中，两种产品均衡的产量相等，均为1/ 4，均衡的劳动投入量为1 /2，高于只能生产X产品时的劳动投入量，此时总效用为1 /2，相比于只生产X产品时也有所提高。根据模型的结果，获取一种生产新产品的新技术使得经济人愿意投入更多的劳动来生产新产品，增加总效用。

3. 带不确定性的自耕农技术选择模型

在现实经济中，新技术往往伴随着很多不确定性，如传统上种植小麦的村庄，在决定是否种植一些棉花时可能面临着很多不确定性。村民们很难在一开始就确切地知道种植棉花所需要的全部工作和最终的产出情况。比如像浇水施肥的操作细节和病虫害等问题，村民可能在初次种植棉花时对这些问题完全没有概念，要等到问题真正发生的时候才会意识到存在着需要解决的问题。那么，将这种普遍存在的不确定性引入自耕农模型将使模型更加符合现实情况，自耕农需要在原技术TX和带不确定性的新技术TY之间进行选择。

首先引入自耕农模型。同简单的技术选择模型相似，假设一个典型的自耕农获得了生产Y（比如生产棉花并制作衣服）的技术设想，我们假设这种初创的产品Y的生产函数存在不确定性，其生产函数为：

Y =F (K ,L )+Uct

其中，按照固定比例，1单位K和1单位L可以生产1单位Y，但存在着50%的不确定性，在上式中用Uct（uncertainty）表示不确定性的存在；也就是说，在一年的生产中，有50%的概率可能顺利得到1单位Y产品，但还有50%的概率生产失败，Y产品产量为0（考虑棉花歉收，衣服可能因为制作得不好而不能穿，或者达不到预期的效果，如美观等情况）；当然，这里的假设隐含着自耕农可以正确地对应用新技术的风险作出判断，这跟现实不完全符合。正常情况下，人们判断一件事情的风险一般是根据历史上的经验来总结规律，不太可能在初次的尝试中就正确地估算出事件的概率，但笔者认为作这样的假设不会对本书关注的主要问题的分析产生严重的影响，因为即使自耕农不能完全正确地预估生产成败的风险，他仍然会跟根据自己认定的成功概率作出行为选择。事实上，当自耕农计划按照一种不完善的既定模式的生产技术进行产品Y的生产时，其能否成功可能取决于一些尚未明确的因素的影响。如表7-1所示：

表7-1　应用新技术的不同结果的发生概率

自耕农要在成熟无风险的生产技术TX和带风险的新技术TY之间作出产量选择。与简单技术选择模型相同，假设自耕农消费Y产品的效用函数与X产品相似，将产品Y引入自耕农的效用函数，则新的效用函数为：

效用函数：

和简单的自耕农技术选择模型不同，由于风险的存在，自耕农在选择产量时的原则会发生变化，从效用最大化转变为预期效用最大化。

自耕农的效用函数为：

由于生产产品Y存在着不确定的结果，因此自耕农的效用成为一个服从均匀分布的离散型随机变量；其期望效用函数可以表示为：

E (U )=U1P (U1)+U2P (U2)

其中1U表示产品Y生产成功时的效用，P(U1) 表示产品Y生产成功的概率；相对地，U2表示产品Y生产失败时的效用，P(U2)表示产品Y生产失败的概率。

与自耕农模型相似的，有：

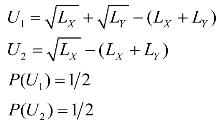
其中，LX表示生产产品X投入的劳动，Ly表示生产产品Y投入的劳动。

由此可知

(www.daowen.com)

显然，当E(U)取得最大值时，有

此时LX =1 /4，Ly =1 /16。相对于简单的自耕农技术选择模型，由于风险的引入，自耕农减少了对产品Y的生产。此时，自耕农的期望总效用E (U)=5 /16。这个结果大于没有引入产品Y时的总效用，小于产品Y无不确定性时的总效用。从不确定性的角度讲，新技术存在的失败风险降低了新技术的应用价值。

4. 自耕农自研发模型

自耕农自研发模型指允许自耕农通过研发投入获得新技术的情况下的模型。自给自足状态下的经济人可能通过引进新的生产技术（生产函数），提高自己的效用。但是新技术设想往往带有很多不确定的因素，从而带来风险。如果直接按照带不确定性的新技术设想进行大规模的尝试，一旦失败可能带来巨大的损失。因此，现实经济中往往有一些很有创意也确实可行的想法没能在一开始就立刻得到实施。一般情况下，人们用一些其他方法对新技术设想的可行性进行试验和评估。这就是研发活动，研发活动的目的是为了减少或消除新技术的不确定性。

当企业家得到一个新技术设想时，他面临三种选择：

①维持原来的技术不变，无风险，无收益变化；

②按新设想生产，风险很大，可能带来收益，但也可能失败，遭受巨大损失；

③进行研发，在有限损失的情况下消除或部分消除不确定性。

因此，自耕农自研发模型描述的是一个自给自足的自耕农在面对一项带不确定性的新技术时，从效用最大化的角度出发是否会先进行研发活动消除新技术的不确定性，之后再应用消除了不确定性的新技术。

自耕农自研发模型可以在带不确定性的自耕农技术选择模型的基础上引入研发活动。生产产品Y的技术仍然是一种带不确定性的新技术，在本模型中，自耕农有可能通过研发活动来消除这种不确定性。

假设1：首先假设研发活动需要投入1 /2单位劳动，且其成功率为50%，即研发投入可能成功也可能失败，研发成功可以得到确定性形式的生产函数：

Y =　F (K ,L)

也就是把带不确定性的自耕农技术选择模型变成了简单的自耕农技术选择模型的情形。显然，不带不确定性的新技术可以使自耕农实现更高的总效用。研发的不确定性如表7-2所示。

表7-2　研发的不同结果的发生概率

同样，为了简化，这里假设自耕农能正确地预测研发活动的成功率，研发的成功率为50%则既不太高也不太低，不至于影响到模型的合理性。在现实经济中，研发的成功率和研发的成本对企业的研发决策有很重要的影响，研发能力同样受到知识和资源的限制，根据舒尔茨对农业技术的考察，过高的研发成本对农民来说可能是无法接受的。研发的成本和成功率之间可能还存在着某种技术上的替代性，如激进的实验和谨慎的观察等。同样出于简化分析的考虑，这里假设自耕农只面对一种固定的研发方式，其研发成功率也是固定的。

如果研发没有任何成本，那么自耕农显然愿意通过消除新技术的不确定性来增加总效用。但研发活动往往是有成本的，在有些情况下成本还非常之高。在模型中，过高的研发成本对于自耕农来所是不可接受的，现实中的研发活动也一样，企业只会选择那些成本可以接受的研发方式，成本极高、超出企业承受能力的研发项目不可能被企业采用。

因此，在假设研发活动需要投入1 /2单位劳动是有合理性的，在这个假设中，研发不需要投入任何资本，主要原因在于：在自耕农模型中，土地资源K是一种比较丰裕的资源，少量的土地资源的投入事实上没有经济成本，不会对自耕农的效用产生影响，而劳动则直接和效用相关，因此假设研发活动只需要投入劳动而不涉及资本可以使模型更加简单。

假设2：自耕农对当期的1单位效用和远期的1单位效用评价相同。

由于引入了研发活动，自耕农面对的选择在研发成功前后会有所不同，在研发成功前自耕农可以在生产产品X、在一定的不确定性条件下生产产品Y和对产品Y进行研发之间作出选择。而当研发成功后，自耕农获得了确定形式的产品Y的生产技术，可以按照简单的自耕农技术选择模型的均衡结果进行生产安排。

可以假设研发活动无法在当期就给自耕农带来效用，即使在第一年研发就获得成功，自耕农也只能从第二年开始应用消除了不确定性的新技术。那么，自耕农在是否进行研发时需要对研发在当期的成本和研发成功后的效用增加之间进行权衡。

因此，模型涉及跨期选择的问题，在这里我们假设自耕农对当期的消费和未来的消费的偏好是相同的。这就意味在不同时期，自耕农的效用函数是完全相同的。这个假设可能并不完全符合现实，成年人可能不像儿童那么喜欢糖，吃一个苹果带来的效用在早上和晚上可能并不相同。经济学家考虑了利率和风险的影响一般认为当期的收入价值高于远期，心理学、社会学等对跨期选择问题也还没有明确的解释。在我们的单人模型世界里，引入利率似乎是没有必要的，因此假设不同时期的效用相同是合理的。

由于创新成功前后自耕农的均衡选择不同，模型的均衡结果也要分情况进行讨论。

首先考虑研发成功前的情况。

在带不确定性的自耕农技术选择模型中，自耕农要投入劳动生产产品X和产品Y，现在自耕农还要另外投入1 /2单位劳动（LR&D）用于研发。

在新的条件下，自耕农的效用函数为：

由于研发成功前，生产Y仍然带有不确定性，因此，仍然有生产成功与失败两种情况。

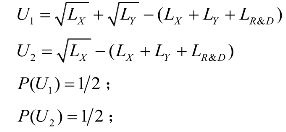
其中，U1表示产品Y生产成功时的效用，　P(U1) 表示产品Y生产成功的概率；相对地，U2表示产品Y生产失败时的效用，P(U2)表示产品Y生产失败的概率。其中，LX表示生产产品X投入的劳动，LY表示生产产品Y投入的劳动。

此时，自耕农的期望效用为：

其中，LR&D =1/ 2，新的均衡解为LX =1 /4，LY=1 /16。由于假设研发成本为1/ 2单位劳动的数值足够小，并没有改变效用最大化时的劳动投入。显然，如果研发成本被假设为3 /4单位劳动或者更高，那么能用于生产产品X和产品Y的劳动量必然后被挤占。引入研发投入后，自耕农的最大化效用E (U)　=-3/ 16，比没进行研发时的均衡结果下降了1 /2。

之后，考虑研发成功后的情况，由于新技术的不确定性已经消除，研发投入不再需要了。此时，自耕农面对的情况和简单的自耕农技术选择模型（2.2）完全相同。此时总效用E (U′)=1/ 2。

综合自耕农自研发模型中研发成功前后的两种情况和带不确定性的自耕农技术选择模型并进行比较可以发现，自耕农进行研发是否能够比采用带不确定性的技术生产Y带来更高的长期总效用，与自耕农的生命能延续多少个周期有关。如果自耕农的生命周期无限长，那么研发成功后每期增加的效用不断累积，研发带来的长期总效用增长就是无穷大的，即使研发的成功率更低一些，进行研发也总是有利可图的。但是现实中人们的寿命是有限的，而且世界是不断变化的，一项新技术不会永远先进，人们要考虑研发得到的新技术是否能在过时之前带来足够的回报，一项研发如果需要很长时间才能成功，成功之后需要很长时间才能收回之前付出的代价，那么在中间发生任何变故都可能导致当初因为研发而付出的效用损失无法弥补。

由此看来，影响自耕农是否进行研发的生命周期长度的临界点在哪里变得很关键。如果该生命周期足够短，比如只有一年时间，那么显然自耕农进行研发没有任何价值。那么，如果该生命周期是两年，三年呢？我们可以计算不同时期自耕农进行研发的预期收益对这个问题进行分析。如表7-3所示。

表7-3　研发和不研发在不同时期期望效用和总效用比较表

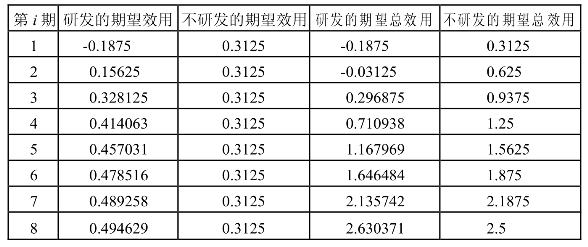
表7-3中研发的期望效用指当自耕农进行研发时，不同时期预期可以实现的效用。随着时间的延长，自耕农始终研发失败的概率越来越小，因此其研发的期望效用越来越接近于1/ 2，也就是研发成功时的均衡效用。而如果不进行研发，则自耕农在整个生命周期中始终按照带不确定性的生产技术生产Y，其每期的期望效用都是5 /16。第三、四列中的期望总效用指从第一期到特定的某一期自耕农各期的效用加总。根据模型的假设，自耕农以整个生命周期的总效用最大化作为自己的决策目标。在模型数值的假定条件下，从第八期开始，进行研发的期望总效用超过了不进行研发的期望总效用。显然，自耕农在考虑是否进行研发时，会考虑生命周期的长短。在本模型中，如果生命周期的长度等于8或大于8，那么自耕农将选择进行研发，一旦剩余的生命周期不足8时，自耕农将放弃研发。例如生命周期为10期，自耕农愿意在前三期进行研发，如果第三期仍然研发失败，那么放弃研发就是一个更加理性的选择。

在自耕农自研发模型中，研发是一种牺牲当前的效用来换取未来更大的效用的行为。这在某种程度上类似于接受教育，上大学需要以几年时间里不能工作、没有收入为代价，但是有可能在毕业之后获得更高的工资水平。如果考虑到上大学存在的学无所成不能毕业的风险，在不十分严格的条件下，读大学也可以理解为对“更高效地使用自己劳动力”的新技术的研发行为。