1. 明确问题

在用AHP分析待解决的问题时，首先要对该问题有明确的认识，将复杂问题概念化，弄清研究对象所包含的各种主要因素，确定各个因素之间的关联关系和隶属关系。

2. 阶梯层次结构模型的建立

根据对问题的分析和了解，将问题所包含的各种因素按照是否具有某些共同的特征加以归纳分组，并把它们之间的共同特性看成是系统中较高层次中的一些因素，这些更高层次中的因素按照另外的共同特性重新组合，直到最终形成单一的最高层次因素。如图3-1所示。

在这个阶梯层次结构模型中，复杂问题被分解成各个元素。这些元素又按照共同属性分成若干组，从而形成不同的层次。同一层次中的元素作为准则对其下属元素起支配作用，同时也要受更高层次元素的支配。这些层次一般可分为三类：

（1）最高层，也称目标层，这一层次只有一个元素，是分析问题的预定目标；

（2）中间层，也称为准则层，也就是为实现预定目标所涉及的各个中间环节，可以由若干层次组成，包括准则、子准则和各种具体指标；

（3）最低层，也称为措施层或者方案层，是指为实现预定目标可供选择的各种措施或决策方案。

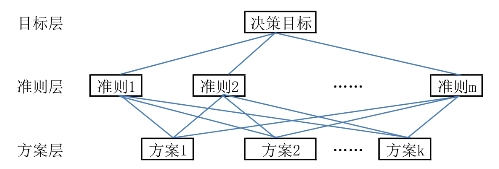
图3-1　简单的阶梯层次结构模型

3. 建立两两比较的判断矩阵

判断矩阵表示在某层次中受上一层次某个元素支配的各个元素之间相对重要性的两两比较。一般取如下形式：

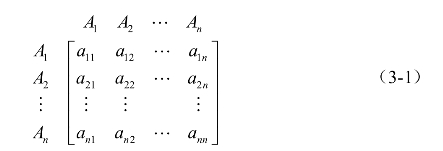
在层次分析法中，为了使矩阵的判断结果定量化，关键在于设法使任意两个方案基于某一准则的相对优越程度得到定量的描述。对单一准则来说，两个方案进行比较一般总是能判断出优劣。在众多的标度方法中，层次分析法普遍采用1～9标度法，对判断矩阵给出数量标度。具体的标度方法为：

比较第i个元素与第j个元素相对于上一层次某个因素的重要性，用相对权重aij进行赋值。以下为标度定义与说明（见表3-2）：

表3-2　1～9标度法

成对比较矩阵具有这样的特点：

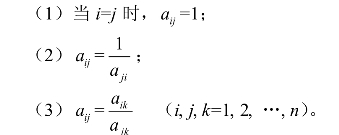
比较判断矩阵中的aij是以历史资料、专家意见和分析经验为根据，再经过反复推敲后确定的。应用层次分析法，保持判断思维的一致性非常重要，只有矩阵中的aij满足上述三条关系式时，判断矩阵才具有完全的一致性。

比较判断矩阵的一致性指标CI（Consistency Index）为

(www.daowen.com)

式中，λmax是矩阵A的最大特征值。一致性指标CI的值越大，表明判断矩阵对完全一致性偏离的程度越大；CI的值越小，表明判断矩阵越接近于完全一致性。一般来说，判断矩阵的阶数n越大，人为造成的偏离完全一致性指标CI的值便越大；n越小，人为造成的偏离完全一致性指标CI的值便越小。

对于多阶的比较判断矩阵，引入平均随机一致性指标RI（Random Index），表3-3给出了1～10阶正互反矩阵计算1000次得到的平均随机一致性指标。

表3-3　平均随机一致性指标RI

当n＜3时，判断矩阵永远具有完全一致性。判断矩阵的一致性指标CI与同阶平均随机一致性指标RI之比称为随机一致性比率CR（Consistency Ratio）。

当CR＜0.10时，便认为判断矩阵具有可以接受的一致性。当CR≥0.10时，就需要对判断矩阵进行调整和修正，使其满足CR＜0.10，从而具有满意的一致性。

4. 层次单排序

层次单排序就是本层次各元素对上一层某元素排出重要性顺序，这需要计算判断矩阵的最大特征向量，方根法与和积法是最常用的两种方法。本书主要介绍方根法。

方根法具体计算步骤：

（1）将判断矩阵的每一行元素相乘，得到公式（3-4）：

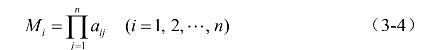
（2）计算　iM的n次方根mi，见公式（6-5）：

（3）将方根向量进行正规化处理，即得特征向量W=（W1 　,W2　,…,Wn）t的第i个分量Wi，见公式（3-6）：

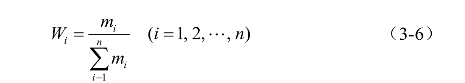
（4）计算判断矩阵的最大特征根，见公式（3-7）：

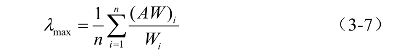
式中，(AW)i 为向量　AW　=（(AW)1,(AW)2,…,　(AW)n ）t的第i个分量。

（5）层次综合排序

利用上述层次单排序的计算结果，经过进一步的综合分析，可以得出对更上一层次的重要性排序。