（1）供应链双方的决策由以上假设条件可知：

制造商的全部期望收益为

即得制造商的决策问题：

类似的，零售商的决策问题为

考虑到环境变量μM（t）、μR（t）、ω（t）、φ（t）等依时间变化时对上述微分对策造成的解析解的求解困难，为简化问题，以下假设各个环境变量均为常数：

（2）微分对策模型与博弈均衡分析

记e*M（t）、e*R（t）分别为制造商决策问题式（5-2）和零售商决策问题式（5-3）的解：

制造商从t时刻的声誉状态Θ（t）之后的收益最优值函数为

零售商从t时刻的声誉状态Θ（t）之后的收益最优值函数为

则有命题：

命题1供应链声誉的微分对策问题式（5-2）、式（5-3）具有Hamilton-Jacobi-Bellman方程：

[证明]

首先考虑制造商的决策：

由最优性原理：

若e*M（s）（t≤s）是制造商的从时刻t、供应链声誉Θ（t）开始的最优声誉维护努力水平，则e*M（s）（t≤s）必是其从时刻（t+Δt）、供应链声誉Θ（t+Δt）开始的最优供应链声誉维护努力水平。

由式（5-4）知

注意到：

对于Δt→0，有

又

将TΠ*M（Θ（t）+Θ′（t）Δt，t+Δt）进行Taylor展开：

将式（5-8）和式（5-9）代入式（5-7），得到TΠ*M（Θ（t），t）的近似：

即得到决策问题式（5-4）和式（5-2）的Hamilton-Jacobi-Bellman方程：

零售商决策问题式（5-5）的Hamilton-Jacobi-Bellman方程可以通过完全平行的分析得到。

至此，命题1得证。

特别的，若记(www.daowen.com)

则有以下命题：

命题2供应链微分对策问题式（5-2）、式（5-3）具有最优供应链声誉微分对策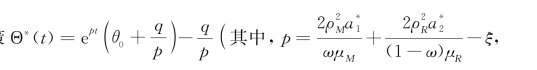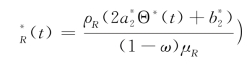，如果关于未知参数a 1、a 2、b1、b2、c 1和c 2的方程组（称之为拟约束方程组）

有解

[证明]

由得

将上面的表达式代入该微分对策问题的Hamilton-Jacobi-Bellman方程（5-6），可得Hamilton-Jacobi-Bellman方程的等价形式：

求解方程（5-12）：

由一阶条件：

将式（5-13）代入式（5-12），得到

注意到以上微分方程组的阶数特点，推测其具有关于Θ的m次多项式形式的解，此时，由于方程左边为m次，右边最高为2（m-1）次，因此，由m=2（m-1）可知m=2。

故设函数ΓM（Θ）、ΓR（Θ）具有以下表达式：

其中，a 1、a 2、b1、b2、c 1和c 2均为未知常数。

将式（5-15）代入式（5-14），得

则由命题已知条件式（5-11）可知方程组（5-16）的解亦为逆约束方程组的解（a*1，a*2，b*1，b*2，c*1，c*2）。

从而函数ΓM（Θ）、ΓR（Θ）具有以下表达式：

将式（5-17）代入式（5-13），即得

将式（5-18）代入状态变化微分方程（5-1），得

解微分方程（5-19）：

记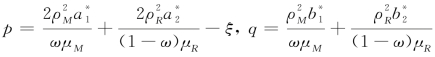，则微分方程（5-19）的通解为

其中，c为任意常数。

从而，根据状态变化微分方程（5-1）中的边界条件Θ（t）|t=0=θ0≥0，可求得Θ（t）满足边界条件的特解：

即

至此，命题2得证。