在供应链双方具有长期合作关系时，对长期利益的期望将可能促使制造商珍惜自己的声誉，进而避免道德风险。

（1）补充的符号说明

◆ θk：零售商在第k（1≤k≤n）期修正后的制造商声誉；

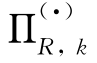◆ 表示制造商在第k期的收益，上标（G）、（L）分别表示制造商提供正常质量产品和低质量产品；

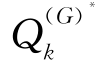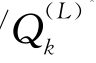◆ /*表示零售商在第k-1期判断制造商向其提供正常质量/低质量产品的条件下在第k期发出的订货量；

◆ （D=DG）表示市场需求量D被零售商观测到为符合正常预期；（D=D L）表示市场需求量D被零售商观测到为低于预期；

◆ （v k=v G）、（v k=v L）分别表示制造商在第k期提供正常质量产品、低质量产品。

（2）补充的假设条件

◆ 供应链双方具有n（n≫1）期合作（期望）；

◆ 由于市场需求混同的存在，制造商提供正常质量产品时，由于市场波动的影响，对该正常质量产品的市场需求有可能比较低，从而导致零售商误认为制造商提供的是低质量产品。类似的，零售商也有可能根据市场需求的现实情况，在制造商提供低质量产品时误认为其提供的是正常质量产品。记制造商提供正常质量产品时被零售商判断为正常质量产品（即导致了正常的市场需求事实）的概率为P（D=DG|v=v G）=α，提供低质量产品时被零售商判断为低质量产品（即导致了低的市场需求事实）的概率为P（D=D L|v=v L）=β。

显然，常数α、β应满足1-α＜β，即制造商提供正常质量产品时，被零售商判断为正常质量产品的可能性应大于被误认为低质量产品的可能性；制造商提供低质量产品时，被零售商判断为提供了低质量产品的可能性应大于被误认为是该质量产品的可能性；并且

基于以上条件，本书建立了制造商的声誉模型并提出以下命题：

命题6（制造商的声誉模型）

制造商具有声誉模型：

即制造商的声誉与其道德有同向变化关系，即如果制造商如果提供正常质量的产品，零售商对其声誉的评价将会升高；反之亦然。

（声誉模型中参数的含义见证明过程。）

[证明]

在供应链双方合作的任一期（如第k期），零售商对制造商的先验声誉评价为θk。在第k期结束时，零售商将根据观测到的事实需求，调整其对制造商的先验声誉评价的判断：

（1）如果零售商观测到了市场需求正常

此时，更新的（后验的）制造商声誉θk+1|（D=DG）可根据条件概率和全概率公式求出：

注意到1-α＜β（或者等价地，1-β＜α），则由式（4-14）可得

即当零售商观测到市场需求正常的事实时，其将向上调整对制造商的声誉的评价，换言之，制造商获得了更高的声誉。

（2）如果零售商观测到了市场需求低

类似于（1），可得

更新的（后验的）制造商声誉：

同样由式（4-15），可得

即当零售商观测到市场需求低的事实时，其将向下调整对制造商的声誉的评价，换言之，制造商获得了更低的声誉。

由（1）、（2）可知：

①若制造商在第k期提供了正常质量的产品（即事件（v k+1=v G）发生），则零售商在第k+1期对其声誉的评价、亦即零售商认为制造商提供了正常质量的产品（即事件（v k+1=v G|v k+1=v G））的概率为

记函数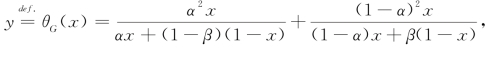显然，θG（x）∈C 2[0，1]，且计算可得其一阶导数：

二阶导数：

特别地，由式（4-17）和式（4-18），可知

将函数y=θG（x）在x=1处进行Taylor级数展开：

由θG（1）=1、θ″G（1）＞0知

从而由式（4-16）和式（4-20）可知

因此，制造商在第k期向零售商提供正常质量产品，并在第k+1期被零售商判断为其提供了正常质量产品的概率将上升，换言之，零售商对制造商声誉的评价将提高。

②若制造商在第k期提供了低质量的产品（即事件（v k+1=v L）发生），则零售商在第k+1期对其声誉的评价、亦即零售商判断制造商提供了正常质量的产品（即事件（v k+1=v G|v k+1=v L））的概率为

同样，类似地，记函数

则θL（x）∈C 2[0，1]，且其一阶导数为

二阶导数为(www.daowen.com)

将函数y=θL（x）在x=0处展成Maclaurin级数：

由θL（0）=0、θ″L（0）＜0知

从而由式（4-22）和式（4-25）可知

因此，制造商在第k期向零售商提供低质量产品将导致零售商在第k+1期将其声誉修正为一个更小的值，即制造商因为道德风险而导致声誉降低。

至此，本书在构建制造商的声誉模型

的基础上证明了命题6。

由声誉模型式（4-26）与命题6，还可以给出以下命题：

命题7（声誉模型的隐性协调作用）

给定不存在道德风险的对称信息情形下制造商的收益满足Q（G）*（c-v G）＞Q（L）*（c-v L），则当供应链合作双方具有足够长期的合作关系时，制造商的道德风险将得到缓解。

[证明]

设在合作中的任一时期k，零售商在期除对制造商声誉的评价为θk，则由式（4-9）知，此时零售商的采购批量Q*k满足

记上式确定的函数为

由命题4，有

此时，在时期k，制造商有两种选择：按协议提供正常质量的产品（无道德风险）、利用道德风险提供低质量产品，相应的收益及后续效应如下：

（1）制造商提供正常质量产品收益为

另外，由于制造商在时期k提供了正常质量产品，从而，按命题6，在时期k+1之初零售商将提高对其声誉的评价，即

且这意味着零售商在时期k+1将提高其订货量：

（2）制造商提供低质量产品

此时相应的收益为

由于制造商在时期k提供了低质量产品，按命题6在时期k+1之初零售商将降低对其声誉的评价，即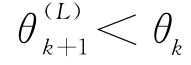。这意味着零售商在时期k+1将缩减其订货量：

由制造商的声誉模型可知：

①对于制造商始终不表现道德风险的情形：

即数列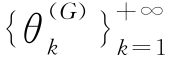为单调递增数列，又由于所有声誉均在区间[0，1]取值，因此，根据单调有界原理可知，该数列必有极限，且其极限即为函数y=θG（x）的不动点。解方程

可求得该不动点为：x=1。即数列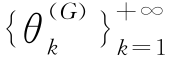的极限为

这说明，在足够长的合作时期中，如果制造商能够始终按契约行事，则零售商将逐渐把制造商的声誉修正为1。

②对于制造商始终完全利用道德风险的情形：

同①的分析，在制造商始终背离契约、提供低质量产品的情形下，零售商对其声誉的修正的评价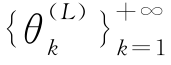是单调递减数列，极限为则由式（4-27）、式（4-28）可知

对于任意小的常数ε＞0，必存在一个正整数N，使得当k≥N时，成立

换言之，零售商相应的批量满足

相应的收益为

注意到Q（G）*（c-v G）＞Q（L）*（c-v L），取ε足够小，有

这意味着，当合作时期足够长（n→+∞）时，必有

即制造商完全遵照协议行事的总收益大于背离协议的总收益，这意味着制造商将不会始终背离协议，从而道德风险得到了部分缓解。

至此，命题7得证。

关于命题7的说明：

①需要指出的是，如果供应链双方有确定合作时期数，则在最后一期制造商必定背离协议；

这是容易理解的，因此，此时制造商已经没有必要维护声誉。

②命题7的条件Q（G）*（c-v G）＞Q（L）*（c-v L）直观上来看是容易满足的，其假设也是自然的：一般而言，供应链向市场提供高质量的产品时，各方的收益自然比低质量产品要来得高。

这就意味着，在零售商没有提供任何激励（或负激励）的情形下，由于制造商对声誉的维护，其道德风险得到了一定程度上的自动控制，这很好地体现了制造商声誉模型的隐性激励作用。