与一次性合作关系不同，在供应链双方具有长期合作期望时，由于非对称信息的事后可验证性，因此，披露非对称信息将变得容易，此时，供应链的最优协调将更可能达到。本部分考虑委托人（制造商）不再采用次优的信息显示机制，而是改为采用“触发战略”（Trigger Strategy）来进行激励的供应链协调过程：假定处于主导地位的制造商对零售商采用触发战略来披露其私有信息，即一旦在未来时期发现零售商没有披露其私有信息，则终止双方的合作关系。

另设：

代理人（零售商）在任一时期不披露其私有信息（即说假话）的行为只可能在下一时期被发现，被发现概率为θ（0＜θ＜1）。

为简化问题，本文假设整体博弈是单一博弈的简单重复，且各期私有信息的分布相同。类似于节4.2.2，对称信息（即真实披露私有信息）下零售商能得到相类似的效用U R，任一期的信息租金为r，任一期不与制造商合作时零售商的保留效应为U-＜U R，则有以下命题：

命题3设制造商与零售商之间具有n（n≫1）期合作期望，若零售商的信息租金r满足，则零售商将始终披露其私有信息；否则，必存在时期m＜n，使得零售商在时期m之前将选择披露其私有信息的真实值，之后将选择报告虚假值。

[证明]

采用逆向归纳法考察一个n（n≫1）期重复主从博弈：

记EΠR，k（T）、EΠR，k（F）分别为零售商在第k时期披露私有信息与披露虚假信息时本时期k及后续时期k+1，…，n的期望收益之和。则

在合作的最后一期，毫无疑问，零售商将选择说假话，因为

类似的，在时期n-1，有

在时期n-2，有

在任意时期k＜n，有通项公式：

先证明命题3的前半部分：(www.daowen.com)

记在时期k（k＜n）说真话（披露私有信息）与说假话（披露虚假信息）的收益之差为Δπk，则由通项公式，有

即收益差值数列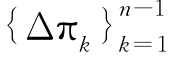为单调递减数列，从而

从而在任一时期说真话都是零售商的最优选择，至此，命题前半部分得证。

后半部分是容易证明的：

若零售商在时期k选择了说假话，则在后续时期，只要还继续合作，它就将一直说假话。

这是因为，若零售商在时期k选择了说假话，即有

则

又

即在时期k+1零售商也将选择说假话，由此，其后续时期仍然会继续说假话。

由于），则至少在时期n-1，零售商将说假话，因此，由逆向归纳可知命题3的后半部分亦为真。

至此，命题3得证。

命题3说明，在具有长期合作期望的简单重复博弈过程中，主导型制造商通过采用触发战略无成本地使得零售商披露其私有信息的真实值、进而实现供应链最优协调是可能的，并取决于事后被识别的概率、信息租金、零售商合作时的单期收益以及不合作时的保留效应之间的平衡关系。