先界定一个概念：

定义1完全分离均衡

对于第3章节3.2.1中的零售商私有信息λ，若在制造商给出的某激励配置集{=（λ，I（λ））|λ∈Λ}下，有I（λ1）≠I（λ2）（∀λ1≠λ2），即不同的代理人在配置集下有不同的选择，则说完全分离均衡存在。

对于长期合作关系下具有跨期关联的非对称信息（零售商私有信息），由于其具有跨期关联性，信息披露对未来时期的影响将使激励问题比一次性的供应链交易情形更加复杂，特别的，在事后不可验证的情形下，有以下结论：

命题2（信息甄别的棘轮效应） 供应链长期合作的重复主从博弈情形下，对于事后不可验证的零售商私有信息，在博弈的第一阶段不存在完全分离均衡，即第3章节3.2.1中命题1的非对称信息甄别机制是无效的。

[证明]

已知生产、经营季节性产品的供应链中制造商与零售商具有长期合作关系，双方在各个销售季节的博弈情形与条件是类似的，即双方具有简单重复主从博弈关系。此时，零售商拥有私有的跨期关联信息λ，制造商具有λ的先验分布信息Λ，Λ为有限集或连续集。其他条件与前述讨论类似。

以整数k（1≤k≤n）记n个合作季节（时期）各自的序号，则类似的，若在时期1制造商给出IC条件（激励契约I（λ））以使得零售商披露λ的真实值：（注：下标中的“1”表示所处时期），则从第二个时期开始，供应链双方将不存在信息不对称，因此，从节4.1.2的讨论可知，在后面时期k中，零售商将取得期望收益不失一般性，设零售商对于未来时期期望收益的贴现因子δ=1。从而首期披露私有信息真实值时零售商所能获得的总收益（同样记为EΠR（T））为

其中，r为零售商获得的信息租金。

注意到Λ中至少有一个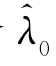≠λ能使得EΠR，k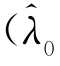）＞EΠR，k（λ）=U R，k，因此，若零售商谎称λ=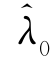，则其能获得的期望收益（记为EΠR（F））为

其中，是零售商在第一时期制造商给出显示机制之后仍然谎称真实值为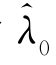时的期望收益。由于该显示机制使得零售商在说真话时才能够获得最大收益，因此，谎称λ=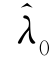将导致零售商第一时期的收益下降，即

记(www.daowen.com)

则由式（4-4）和式（4-5），有

显然，因此可以断言，具有足够长时期的合作期望下制造商给出的显示机制将不但不能使得零售商披露其真实值，反而会刺激其说谎的冲动。

至此，命题2得证。

命题2揭示了长期合作关系中非对称信息甄别问题的棘轮效应。

由于信息隐匿可以给信息拥有者带来信息租金，因此，甄别非对称信息将给委托人带来损失，而要在甄别信息的同时实现供应链利润的最大化则面临更大的困难；更进一步的，考虑到信息披露对代理人未来收益的影响，棘轮效应的影响将使得供应链最优协调成为一个系统性难题。因此，克服棘轮效应的影响具有重大意义。一般地说，可以提出以下思路来消除或缓解信息甄别的棘轮效应。

（1）全局信息显示机制。

即将第3章节3.2.1中的激励相容条件从第一期拓展至所有时期：，但是这将带来的问题是零售商全局收益函数难以确定，同时，代理成本过高，因此存在着实用性的疑虑；（2）引入多代理人竞争机制。如拍卖机制。

引入类型相关的多个代理人、通过代理人之间的竞争来揭示代理人私有信息，委托人可能攫取几乎全部理论收益。

（3）引入充足统计量（Sufficient Statistic）。

当代理人（零售商）具有私有信息，委托人（制造商）通过寻找事后可观察的、与具有一定相关性的某个随机变量来对代理人进行威慑，有利于信息的披露。