考虑报童模型中制造商向零售商提供基于批发价和回购价的回购激励策略。同时，为控制对季末积压产品进行回购时所产生的额外成本，制造商认为在季末需要回购时委托零售商进行积压产品的处理是更有利的。

零售商具有私有信息即自身的期末库存产品的残余价值s，而制造商不了解s的具体数值，仅知其先验概率分布G（x）及其密度函数g（x）。

具体的，设已知：

该季节性产品的制造成本为v，市场销售价为p，相应的市场需求服从均匀分布U[0，M]（M为正常数），分布函数和密度函数分别为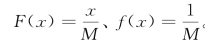。零售商知道自身的季末库存积压产品的残余价值s，而制造商仅知s的先验分布为均匀分布U[0，m]，即

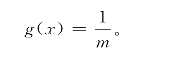
1.集中决策模式

类似于节3.1.1，在追求供应链整体期望收益最大化的集中决策模式下，经过简单的计算可得

最优供货批量：

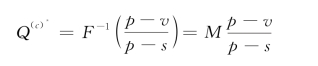
供应链最优期望收益：

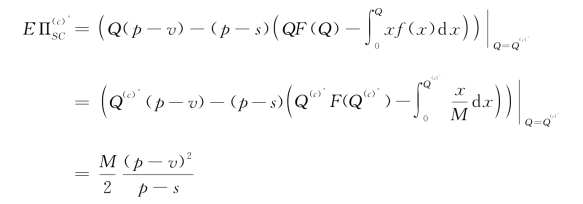
2.信息对称时的回购激励模式

同样，类似于节3.1.1计算可得

零售商的期望收益：

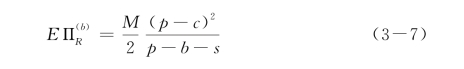
相应的最优订购批量：

制造商的期望收益：

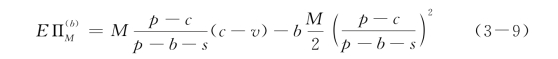
3.信息不对称对最优回购激励策略的影响

针对零售商所声称的残余价值s，制造商给出相应的激励配置集合（激励菜单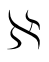）{=（c（s），b（s））|s∈[0，m]}。此时，如果处于信息对称情形，则由零售商的期望收益函数

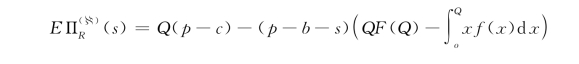
可知其最优批量为

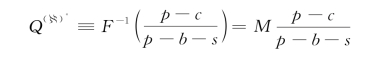
相应的最优期望收益为

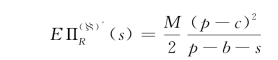
根据显示原理式（3-5）中的IC条件可知：

零售商披露私有信息（说真话）的期望收益函数为

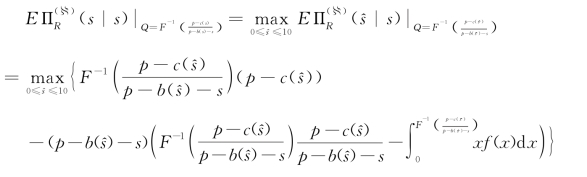
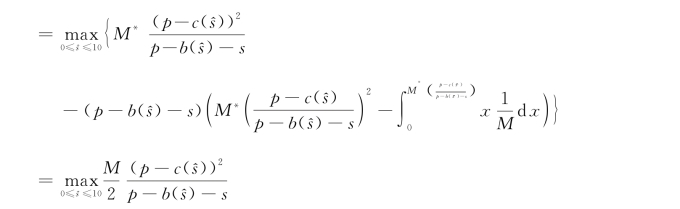
这意味 着，s^=s是 零 售 商 说 谎 的 期 望 收 益 函 数的最大值点，从而其一阶导数应满足

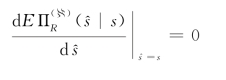
亦即

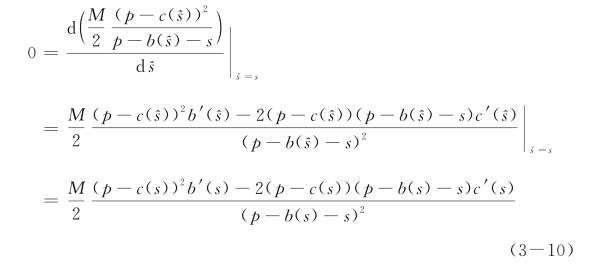
即

另外，最优性还要求必要的二阶条件，即其二阶导数应满足

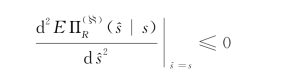
亦即

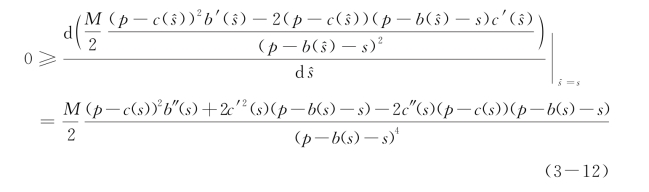(www.daowen.com)

对式（3-10）就变量s两边求导、代入式（3-12）、并结合式（3-11）化简，可得

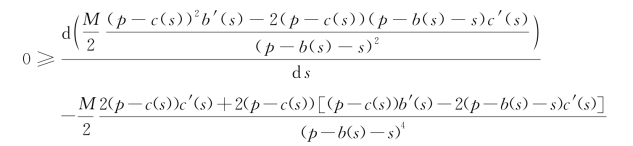
即

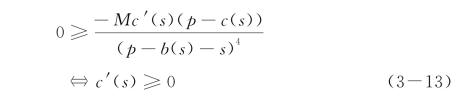
即证明了以下命题：

命题10若回购激励契约=（c（s），b（s））|s∈[0，m]}满足式（3-11）和式（3-13），则该激励契约能揭示零售商的私有信息。

另外，由微分方程（3-11），根据节3.1.1中对命题5及推论4的讨论可知，若在期末积压库存产品残余价值s信息不对称时，仍然存在基于批发价和回购价组合（c，b）的最优协调策略，则制造商和零售商将达到对最优供应链整体收益的分配比例δ（δ已由双方的实力等因素决定），并且由可知：

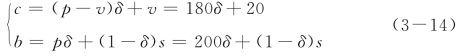
将式（3-14）代入式（3-11），得

式（3-15）显然是不成立的。这说明最优协调无法达到，即验证了命题9的①。

4.算例分析：信息不对称对回购激励力度的影响

接下来分析期末积压库存产品残余价值s信息不对称对制造商的回购激励策略和各方的期望收益的影响。

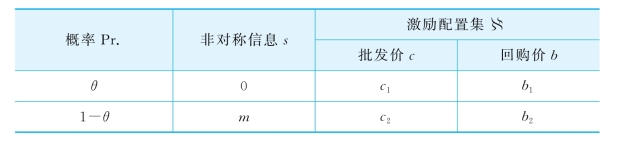
为简化问题，设非对称信息s的概率分布退化为两点分布：P（s=0）=θ，P（s=m）=1-θ。对此，激励方（制造商）基于回购激励方式提出激励配置集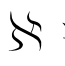满足：

表3-4　制造商的激励配置集

根据式（3-5）中的IC条件和式（3-7）可知

须满足

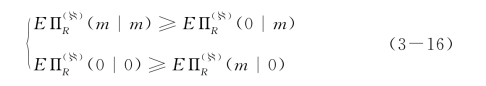
此时，零售商将披露其私有信息s。

又由式（3-5）与式（3-9）可知，制造商的决策问题为

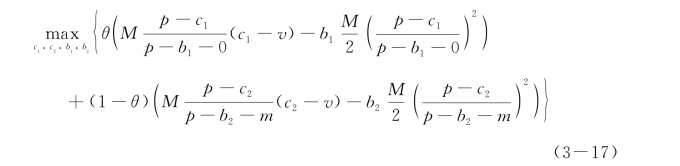
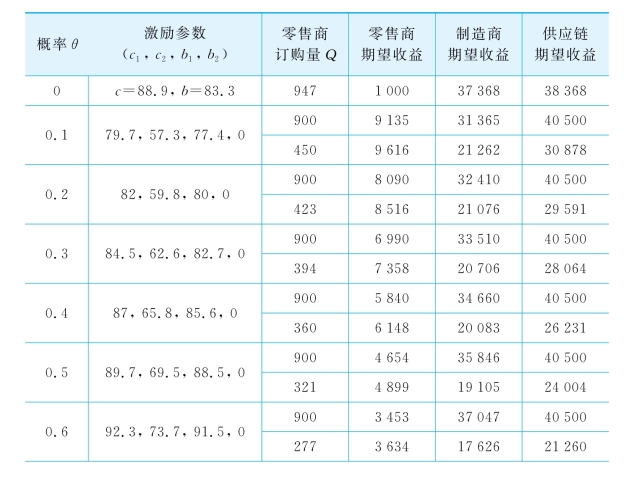
给定相关参数值（v=10、p=100、M=1 000、m=5）之后，可以解约束规划问题式（3-17）（表3-5）。

表3-5　信息不对称与信息对称情形各方收益的对比

续　表

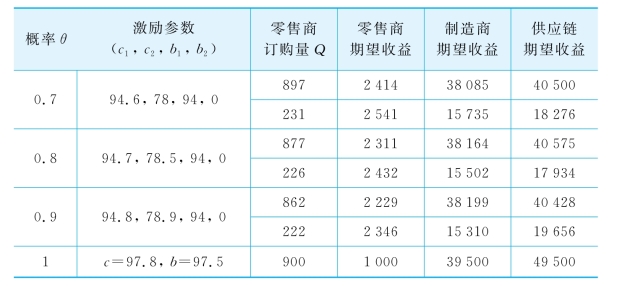
注：①任意概率对应的两行中上行为（s=0），下行为（s=m=5）；
②设零售商保留效用为1 000。

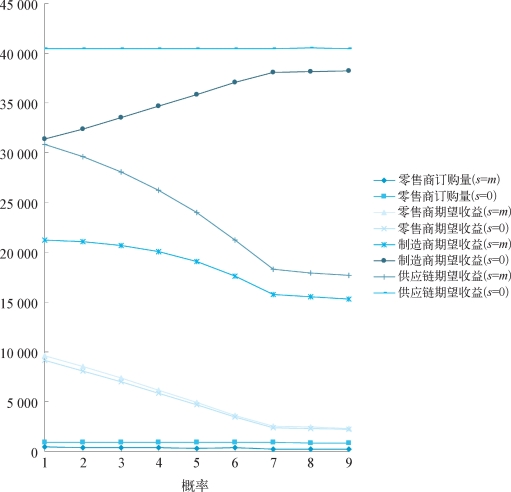
图3-4　（s=0）与（s=m）时的数据对比

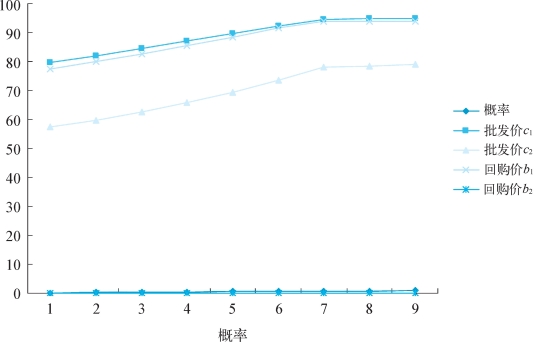
图3-5　（s=0）与（s=m）时的激励变量对比

从图3-4和图3-5中，可以看出：

①随着制造商对零售商的私有信息（积压产品残余价值）s的取值为s=m的信念上升（即θ增大），其给予零售商的激励契约菜单中的两对参数（c 1，b1）和（c 2，b2）也在不断上升；

②（s=0）时，不管制造商对s的取值的信念如何变化，零售商订购量始终稳定在900左右；而（s=m）时，随着制造商误认为其为（s=0）型零售商的信念θ上升，零售商的订购量不断下降，且所有订购量均远大于（s=0）时；

这一现象说明：

对于（s=0）型零售商，由于不管制造商信念θ如何变化，它均处于有利可图的地位，而对于（s=m）型零售商，若它被制造商识别的把握越低，则它越没有动力订购适当的货物批量，也就越不利于供应链收益的最大化，即达到供应链协调。

③（s=0）时，随着制造商对s的取值为s=0的信念上升，其收益单调下降；但均大于信息对称时。这说明零售商得到了私有信息的信息租金，并且信息租金的数值随制造商误认的信念而上升。