从已有的文献来看，多数学者采用某种综合评价方法对立项项目进行评价，但是从本章第6.1节和第6.2节所应用的评价方法结果看，采用不同的评价方法对同一组对象进行评价所得到的结果往往存在一定程度的差异，也就是单一评价方法之间的非一致性问题。如果将这些单一评价方法进行组合，就要对单一评价方法的评价结果进行事前一致性检验，检验通过后方可进行组合评价，在组合评价得到结果后还要对其进行事后的一致性检验，具体步骤如下：

1.组合评价方法一致性检验的步骤

组合评价方法流程如图6-2所示。

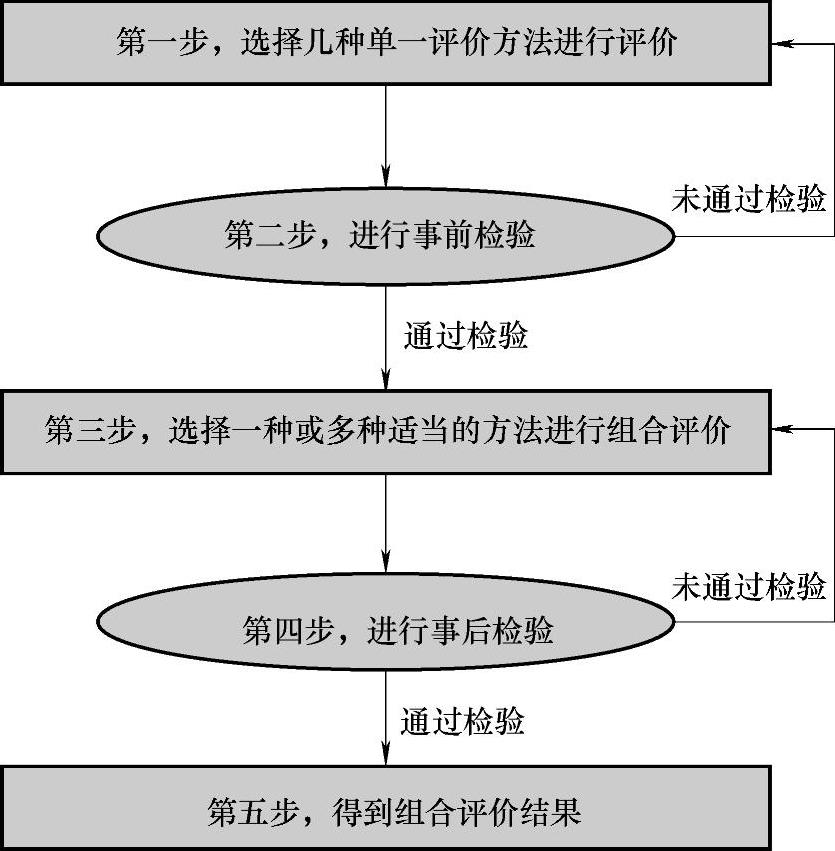
图6-2 组合评价方法流程

第一步，选择几种单一评价方法进行评价。

之所以要对组合评价方法做事前检验，是因为只有通过单一评价方法评价结果一致性检验，即采用的多种单一评价方法的评价结果虽然不完全一致，但却能相互验证，它们的组合评价才能得到可信的组合评价结果。通常情况下，组合评价前的一致性检验采用等级相关系数法，即对不同的单一评价方法的评价结果进行一致性检验。

假设用m种评价法对n个评价对象（项目）进行评价，所得评价值的排序情况见表6-9。

表6-9 m种方法排序一览表

y_ij表示第i个评价对象在第j个评价方法下的排序：

1≤y_ij≤n（i=1，2，…，n，j=1，2，…，m）

第二步，进行事前检验。

1）对各单一评价方法提出假设。假设

H₀：m种评价方法不具有一致性

H₁：m种评价方法具有一致性

2）构造统计量。

①当n≤7，构造统计量为

式中，统计量S为Kendall一致性系数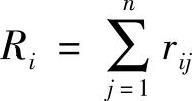，，r_ij是被评价对象i在第j种单一评价方法下所排的位次。在给定的显著性水平下，可查得Kendall的一致性系数临界值S_α。当S>S_α时，则拒绝原假设，可以认为这几种评价结果关系密切，即认为这几种评价结果具有一致性，通过了组合评价的事前检验。

②当n>7，构造统计量为

χ²=m（n-1）W （6-7）

式中，χ²近似服从自由度为n-1的χ²分布

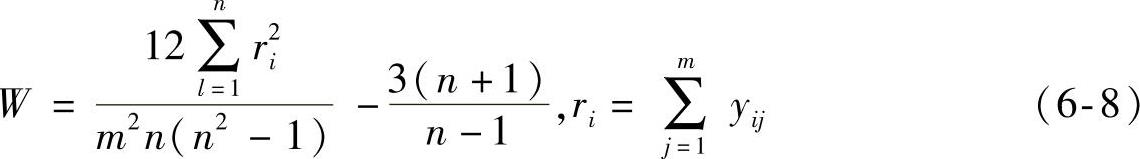
协和系数W可反映实际符合与最大可能符合之间的差异。

3）检验。服从自由度为n-1的χ²分布，在给定的显著性水平α下，查表得临界值χ²_α/2（n-1），当χ²>χ²_α/2（n-1）时，则拒绝H₀，也就是要接受H₁，即认为各种单一评价方法在α显著性水平上具有一致性。本书中n=10，选用公式（6-7）中的χ²为统计量。

Kendall一致性系数法对单一评价进行一致性检验，可以检验各种单一评价方法评价结果总体上是否具有一致性，该检验通过验证协和系数W，来考察多种评价方法对评价对象的评价结果是否具有一致性。

第三步，选择一种或多种适当的方法进行组合评价。通过事前检验后，选择适当的组合方法对已得到的多组单一评价结果进行组合评价，并得到一种或多种组合评价的结果。

第四步，进行事后检验是用来对组合评价方法所得的评价排序结果进行合理性检验，查看组合结果是否与原单一评价方法的结果间具有一致性。如果在第三步中采用了多种组合评价方法时，在这一步还可以凭借事后检验得到与之前单一评价方法的评价结果最具有一致性的评价结果，即选出最合理的组合方法。对于组合评价的事后检验，通常会使用Spearman等级相关系数法。

具体步骤如下：

（1）原假设H₀：第j种组合方法与原n种单一评价方法所得到的评价结果无关。

备择假设H₁：第j种组合方法与原n种单一评价方法所得到的评价结果相关。

（2）对之前的假设进行检验，计算检验统计量：(www.daowen.com)

1）当m<10时，检验统计量为

式中，ρ_jk表示第j种组合评价方法与原第k种单一评价方法间的Spearman相关系数，ρ_jk越大表明相关程度越高，ρ_jk越小则相关度越低。ρ_j表示第j种组合评价方法与原n种单一评价方法排序结果间的相关系数。

2）当m≥10时，检验统计量为

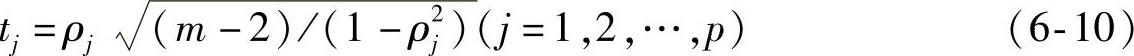
式中，ρ_j与t_j相同，服从自由度为m-2的t分布。

在给定的显著性水平下（本书中取α=0.01），当统计量大于临界值则拒绝原假设，认为组合后的评价结果与原各单一评价结果间关系密切，即通过事后检验。

第五步，得到组合评价结果。在通过了前面第三步的事前检验后，当第三步中采用的组合方法只有一种时，通过这样一次单一方法进行事后检验就意味着可以接受此组合评价结果；但当组合评价方法不止一种时，即需要分别对不同的组合评价结果进行检验，也就是将多个组合评价结果分别对原评价结果进行检验，其目的是要在多种组合评价结果中选择出一种最理想的组合评价结果。

2.农业科技项目中应用离差最大化组合赋权法组合评价的一致性检验

按照上文介绍的组合评价一致性检验的步骤，结合本书实际算例，结果如下：

第一步，根据本书第4、5章所得到的评价指标与基于离差最大化的组合赋权的权重，分别应用层次分析法、熵值法、离差最大化组合赋权评价法以及TOPSIS法和模糊综合评价法对应用开发类10个申请书进行综合评价，各排序结果见表6-7。

第二步，应用式（6-7）、式（6-8），对表6-7中各评价方法得到的评价顺序进行组合评价的事前检验，经计算W=0.98，χ²=m（n-1）W=5×（10-1）×0.98=44.1，在给定显著性水平α=0.01，查表得临界值χ²_α/2（9）=21.666，显然χ²=44.1>21.666=χ²_α/2（9），χ²大于χ²_α/2，因此拒绝原假设，即在给定的α=0.01的显著的水平下，不能认为五种单一评价方法不具有一致性，也就是说在给定的显著性水平下这五种单一的评价方法具有统计学意义上的一致性。

第三步，分别应用平均值法、Borda法和Copeland法对已得到的五个单一评价法结果进行组合评价，得到的组合评价结果见表6-10。

表6-10 组合评价结果（基于离差最大化的组合赋权法）

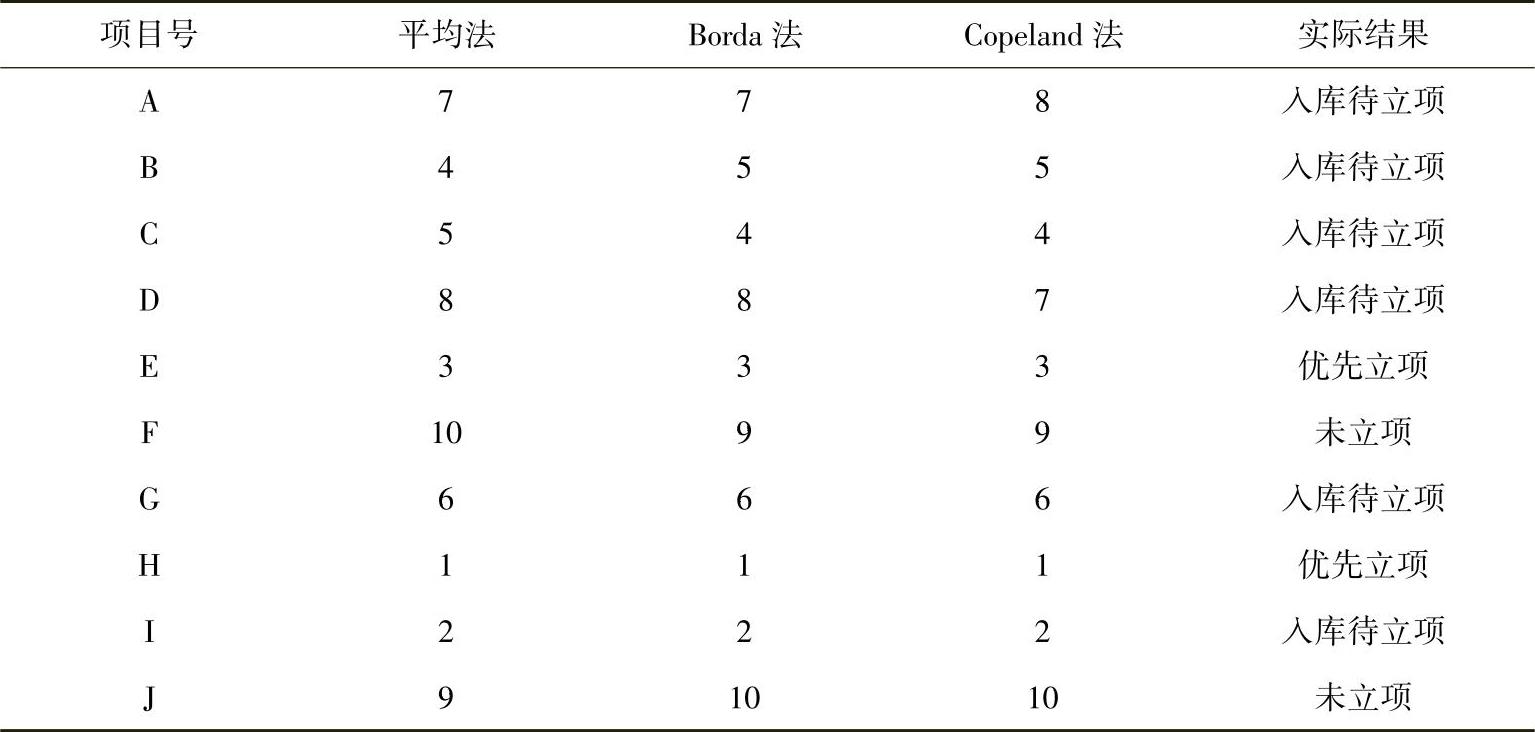
第四步，在分别获得单个评价模型和组合评价模型的结果后，应用式（6-9）和式（6-10），分别计算了平均法、Borda法和Copeland法的t值，并分别用t_a、t_b、t_c表示，通过SPSS21.0计算，得到t_a=8.108、t_b=7.431、t_c=7.134，在显著性水平α=0.01情况下，查得临界值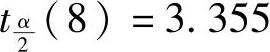，显然t_a、t_b、t_c都大于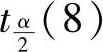，所以说三种组合评价方法与五种单一方法密切相关。此外，从t值的大小可知，从组合评价结果与单一评价结果相关性角度看，平均值法优于Borda法和Copeland法，因此取平均值法的评价结果为最终排序。从实际情况的定性评价结果看，该模型的结果和实际的结果一致。

第五步，得到的五种单一评价与三种组合评价的Spearman相关矩阵为

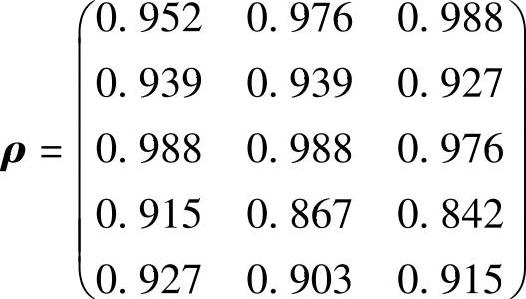
可知，如果将最优的平均数评价组合法作为评价结果，该结果与实际定性评价的结果一致。从Spearman相关系数可以看到对于单一的（综合）评价方法来说，基于离差最大化的线性评价结果与其最相近。也就是离差最大化赋权评价法≻层次分析法≻熵值法≻基于离差最大化赋权的模糊综合评价法≻基于离差最大化赋权的TOPSIS法。

3.农业科技项目中应用层次-熵值分层组合赋权法组合评价的一致性检验

与上文的内容和步骤相同，检验过程及结果如下：

第一步，根据本书第4、5章所得到的评价指标与基于层次-熵值分层组合赋权的权重，分别应用层次分析法、熵值法、离差最大化组合赋权法以及TOPSIS法和模糊综合评价法对应用开发类10个申请书进行综合评价，各方法得分及排序结果见表6-8。

第二步，运用式（6-7）、式（6-8）对表6-8中五种单一评价方法的排序结果进行一致性检验，经计算W=0.99，χ²=m（n-1）W=5×（10-1）×0.99=44.6，在给定α=0.01的显著性水平下，查表得临界值χ²_α/2（9）=21.666，显然χ²=44.6>21.666=χ²_α/2（9），因此拒绝原假设，即在给定α=0.01的显著性水平下，不能认为这五种单一评价法不具有一致性，也就是说这五种单一评价法具有统计学意义上的一致性。

第三步，在通过了第二步的事前一致性检验后进行组合评价，分别应用平均值法、Borda法与Copeland法对已得到的五个单一评价法结果进行组合评价，由此得到的组合评价结果见表6-11。

表6-11 组合评价结果（基于层次-熵值分层组合赋权法）

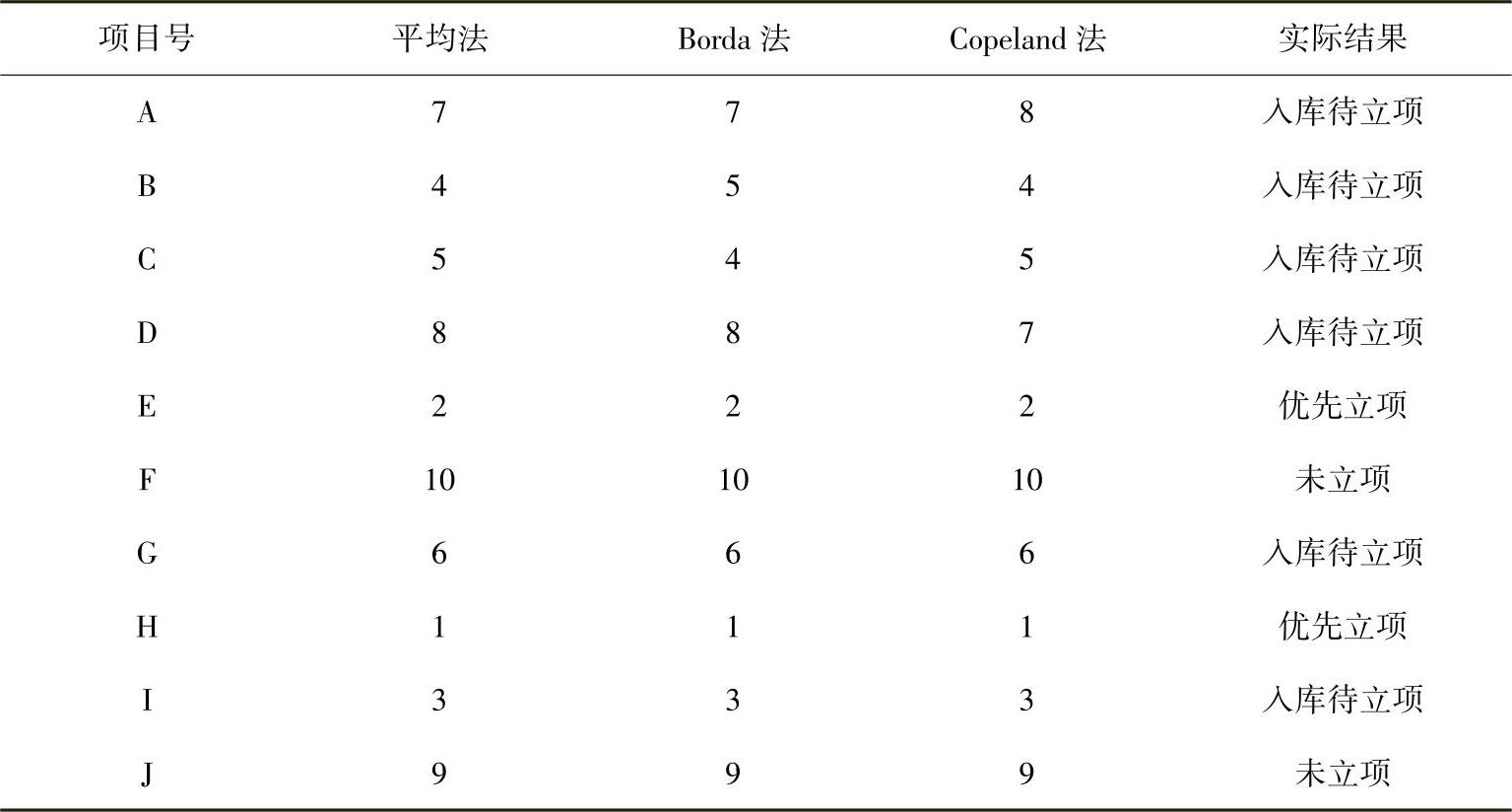
第四步，在分别获得单个评价模型和组合评价模型的评价结果后，应用式（6-9）和式（6-10），分别计算组合评价方法——平均法、Borda法和Copel-and法的t值，分别用t_a、t_b、t_c表示。经SPSS21.0计算，分别得到t_a=9.571，t_b=9.262，t_c=9.000，在α=0.01的显著性水平下，查得临界值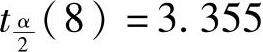，显然t_a、t_b、t_c都大于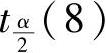，所以说三种组合评价方法与之前的五种单一评价法密切相关。此外，从t值的大小可知，平均值法优于Borda法，Borda法优于Copeland法。那么在本例中，选择平均值法的排序结果为最终结果，该结果与起初对项目的实际定性评价结果基本一致。

第五步，在通过了事前、事后一致性检验后，得到三种组合评价结果分别与之前的五种评价结果的Spearman相关矩阵：

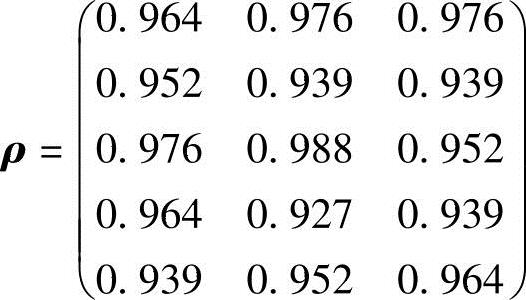
从Spearman相关系数可以得到三种组合法对五种单一法结果的Spearman相关系数。以平均值法为最终评价结果，由ρ矩阵中的第一列可以看到：基于分层组合赋权的组合评价结果与其最相近，也就是说基于分层组合赋权的综合评价法≻层次分析法=基于分层组合赋权的TOPSIS法≻熵值法≻基于分层组合赋权的模糊综合评价法。

经研究结果表明，基于分层组合权重的评价模型能够在多个评价模型中达到最大的一致性，从而有效地减少了群决策中不同主客观评价法的“极化”效应。