在实际应用中评价者对同一个评价对象运用多种不同的评价方法分别进行评价时，就可能出现一个很现实的问题，即各个评价方法所得到的结论存在差异。针对这样的非一致性问题，有学者提出了对各单一评价方法所得到的排序名次值进行重新组合的组合评价方法，其中比较成熟、常见的组合评价方法包括平均值法、Borda法、模糊Borda法以及Copeland法等。唐俊等在给出组合评价方法的有效性定义的基础上，提出了平均值法、Borda法以及Copeland法的组合评价方法有效性的思路，为组合评价提供了理论与现实的指导。徐泽水等提出了使最终评价结果与之前所得的各单一法差距最小的最小距离法。陈衍泰、陈国宏等提出了基于两阶段复合思路的组合评价方法。郭亚军等认为存在一种最佳评价结果，该结果使得各评价方法结果与其方差最大。可见，针对单一评价方法不全面的问题，组合评价方法已经得到了大力的发展。组合评价方法是在已有评价结果的基础上，对评价对象进行更全面、更合理的评价，特别适合考察重点为创新度的项目评价上，由于此类项目容易产生非共识的情况，因此，通过组合评价，尽可能地集结各单一评价方法的评价结果，进一步减小评价结果不全面的概率。

组合评价方法综合利用了评价对象各个方面的数据信息，将不同的评价方法所得到的评价值或由不同的评价方法所得出的评价排序进一步组合，通过运筹学的处理，得到最佳评价结果，最终实现对评价对象整体性、准确性、客观性的认识。因此说，组合评价的实质是将不同的评价方法进行合理组合，得到最佳评价结果，尽可能地提高评价水平和评价精度。目前，在经济管理等众多领域，都逐渐开始实行组合评价方法，但目前农业领域特别是农业立项项目的组合评价还很少见。

下文为讲解方便，设y_ij为用第j种单一评价方法得到的项目（方案）x_i的排序值。

1.平均值法

将排序值转换为分数，第1名得n分，第2名得n-1分，…，第j名得n-j+1分，…，最后一名即第n名得1分，即

R_ij=n-y_ij+1（i=1，2，…，n；j=1，2，…，m）

其中如有相同的名次，则取这几个位置的平均分；之后计算不同评价方法下各方案得分的平均值R_i：

再按每个项目R_i进行排序。如果出现两个方案R_i=R_s，则计算不同方案下得分的方差σ_i，

取方差最小者为优，方差大者次之。

2.Borda法(www.daowen.com)

若单一的评价结果认为x_j劣于x_i的个数大于认为x_j优于x_i的个数，则记为x_i>x_j，若两者个数相等，则记x_i～x_j。

令B={b_ij}_n×n，其中，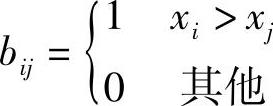

那么，方案（项目）x_i的得分为

按照b_i的大小给x_i进行重新排序，在这一过程中如有b_i=b_j，取方差略小者为优，方差大者次之。

3.Copeland法

Copeland法与上述的Borda法不同之处就在于计算“优于”次数的同时还要计算出“劣于”的次数，其计分规则为

那么，方案（项目）x_i的得分为

按照c_i的大小对x_i进行排序，若出现c_i=c_j，同样，取方差小者为优，方差大者次之。

以上是三种常见且被证明其有效性的组合评价方法，要解决多种单一方法评价结论的不一致问题，就要在已有的评价结果具有一致性的基础上，对其进行组合评价，得到组合评价后还要进行有效性分析与比较，从而确定使用哪一种组合评价方法所得到的结果是最有效的。