上文在层次分析法与熵值法的基础上分别求得了离差最大化组合赋权法以及层次-熵值分层组合赋权的权重，结果见表5-6。

表5-6 层次分析法、熵值法及离差最大化与层次-熵值分层组合赋权权重

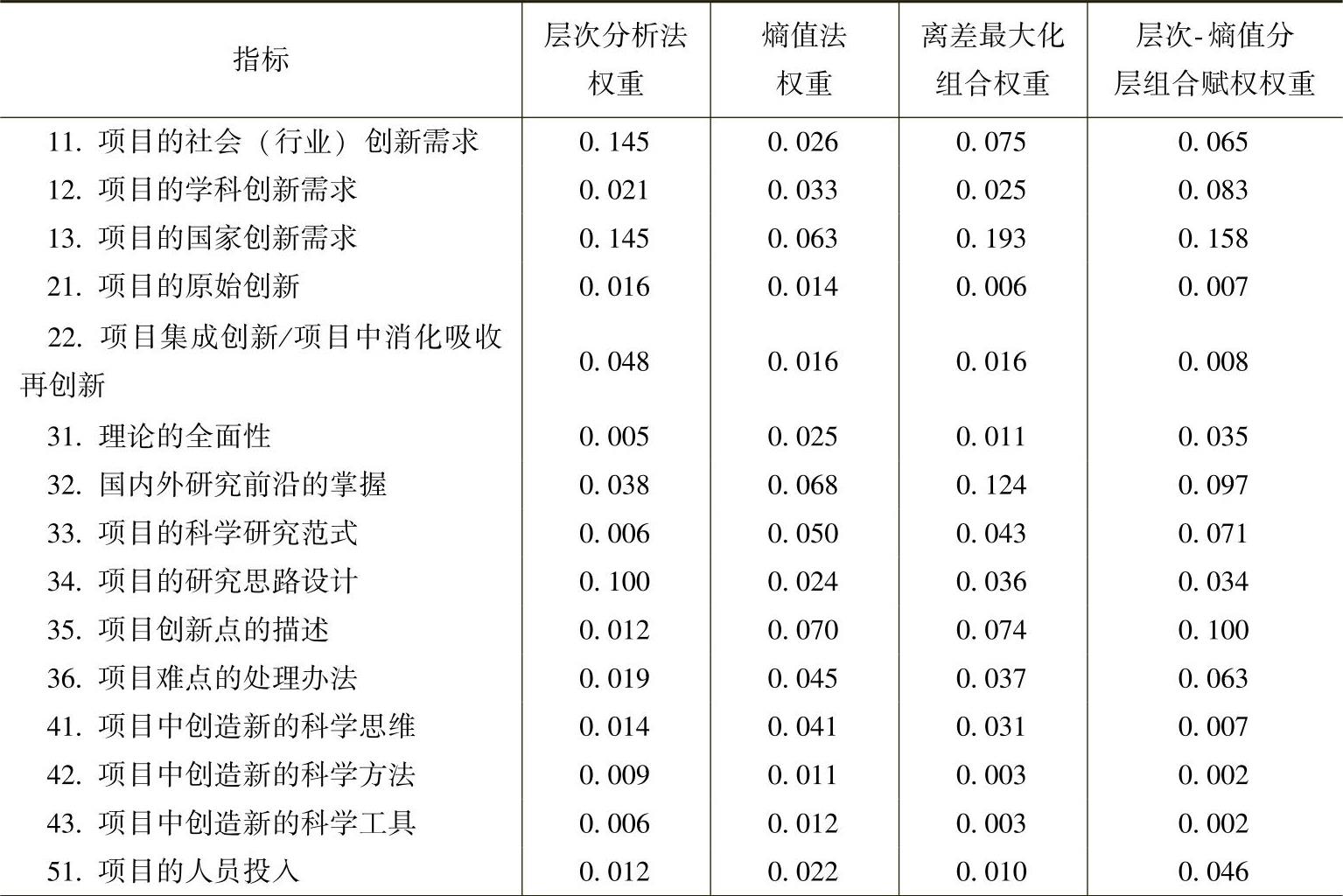
（续）

离差最大化组合赋权和分层组合赋权与层次分析法权重具有较为相似的趋势，其中两种组合赋权均起到了放大指标差异的作用，而分层组合赋权法得到的权重较离差最大化组合赋权更为缓和，如图5-5所示。四种赋权方法所得到的权重两两相关的Spearman相关系数见表5-7。

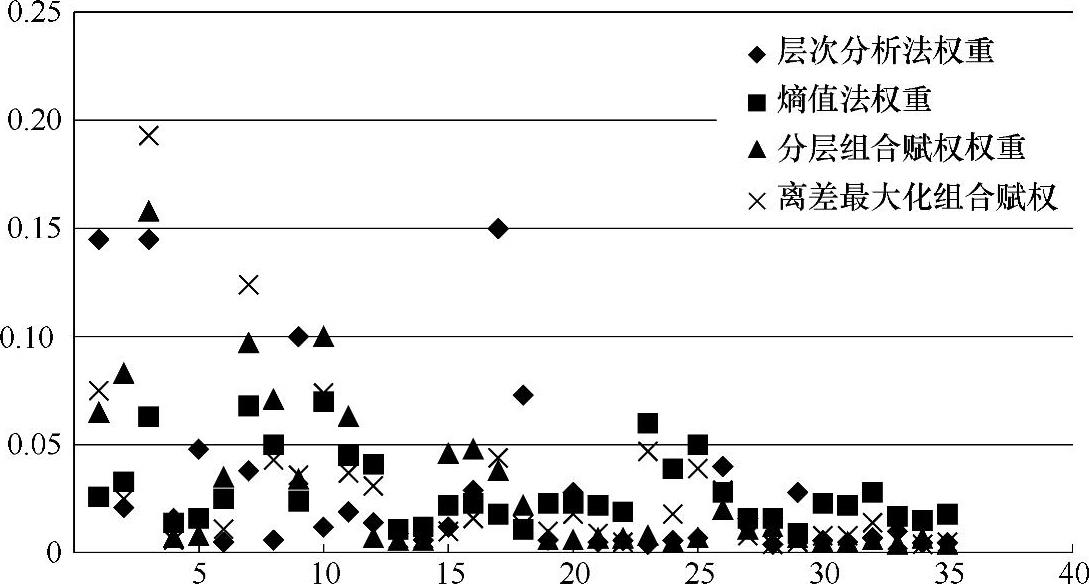
图5-5 四种赋权法的散点比较(www.daowen.com)

表5-7 四种方法所得权重的相关系数（Spearman相关系数）

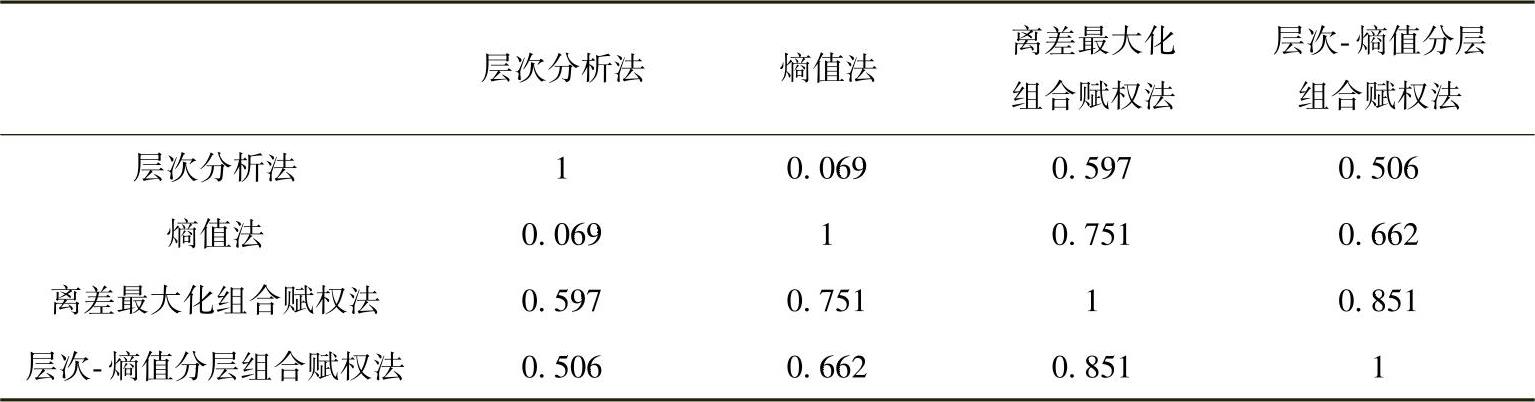
从表5-7可以看出层次分析法与熵值法在赋权上的相互独立，是由其方法本身的原理决定的，而离差最大化组合赋权法与层次-熵值分层组合赋权法相关性较高，主要是因为二者均为建立在层次分析法与熵值法基础之上的组合赋权法。此外，对离差最大化组合赋权法和层次-熵值分层组合赋权法进行差异化t检验，将两种赋权方法无差异作为H₀假设，得到结果表5-8。

表5-8 成对双样本方差分析的t-检验结果

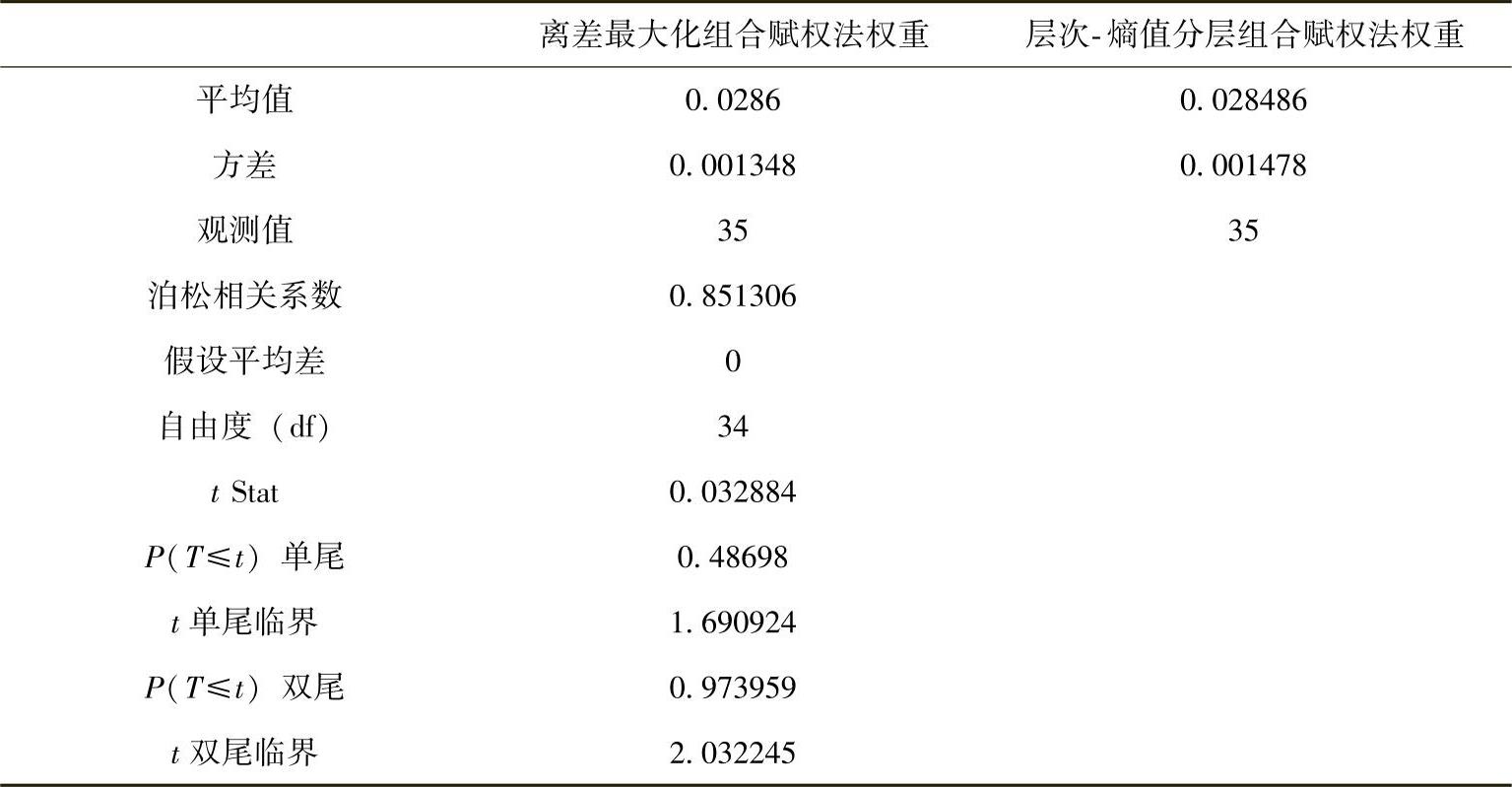
可见，P值为0.973959>0.05，故接受H₀，即认为两种赋权法差异不显著。从差异化检验的结果来看，本书所提出的层次-熵值分层组合赋权法与经常使用的离差最大化组合赋权法相比差异并不大，但因其在一定程度上对权重分布的分散度有所收敛，所以说这种分层赋权的方法既保证了权重的有效性，也收到了收敛权重分布的效果。