层次分析法是由专家衡量既有指标相对重要性的主观赋权法，专家需要熟悉指标体系，做出具有权威性和代表性的评判。同时，因为是直接针对指标打分，相对于熵值法来讲确定的权重稳定并可用于立项评价。熵值法则是一种相对客观、具有动态性的评价方法。为了综合两种方法的优点，根据实际情况选用最适用的数学模型集结两种权重并得到组合权重。本书采用的基于层次分析法和熵值法的离差最大化的组合赋权法，是将评价对象的指标赋予不同权重。

本部分选择离差最大化组合赋权的一个基本思想是使各决策方案的多属性综合评价值尽可能分散。本书以应用开发项目为例。

1.离差最大化组合赋权法

组合权重为w=αU+βV，其中w=（w₁，w₂，…，w_m）^T，α、β分别表示为层次分析法和熵值法权向量的系数，且α≥0，β≥0。运用离差（方差）最大化的原理，令α、β满足单元化的约束条件，即α²+β²=1。在已经得到了层次分析法权重U和熵值法V的情况之下，想要得到组合权重w，就只需确定α和β即可。本书运用离差最大化的原理，构建如下线性规划模型，求解α、β的值：

s.t.α²+β²=1，α，β≥0，且α、β不能同时为0

其中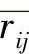，表示第i个指标的平均值。

构建拉格朗日函数求解最优化问题，需要引入拉格朗日乘子λ，即

分别对α、β求一阶导数，令∂L/∂α=0，∂L/∂β=0，则有(www.daowen.com)

另有α²+β²=1，可得

即可得到组合权重（未归一）w=αU+βV，再对w=（w₁，w₂，…，w_m）^T进行归一化处理，可得到最终的w^∗=（w₁^∗，w₂^∗，…，w_m^∗）^T为最终的权重，根据该权重可得到各个项目的综合评价值，并以此进行比较：

2.组合赋权在农业科技项目创新性评价中的应用

本书对35个二级指标使用熵值法，对9个一级指标采用层次分析法，这样既保证了专家对于指标权重的主观判断，也保留了熵值法得到的对客观申请书的整体评价。

通过w=αU+βV，可得到未归一的权重，对该权重进行归一化处理，得到w^∗，现记为

W_d=（0.075，0.025，0.193，0.006，0.016，0.011，0.124，0.043，0.036，0.074，0.037，0.031，0.003，0，003，0.010，0.016，0.044，0.013，0.010，0.018，0.009，0.005，0.047，0.018，0.039，0.029，0.008，0.004，0.005，0.008，0.008，0.014，0.006，0.004，0.005）T