结构方程模型（Structural Equation Modeling，SEM）起源于Sewall Wright提出的路径分析概念。它是基于变量协方差分析潜变量内部结构的多变量测量解释模型，是对计量经济学、计量社会学与计量心理学等领域的统计分析方法的综合。结构方程模型中的因子分析不能完成探索性的工作，是一种验证性的方法。在实际研究中，验证性因子分析是要根据具体的研究问题设定一个理论模型，然后通过对数据的收集与处理，进行因子分析模型的拟合，当模型拟合效果不好或拟合参数不能通过统计检验时，就要对原有模型进行逐步修正，直至达到模型拟合指数的相关要求。结构方程模型运用（验证性因子分析）流程如图4-2所示。

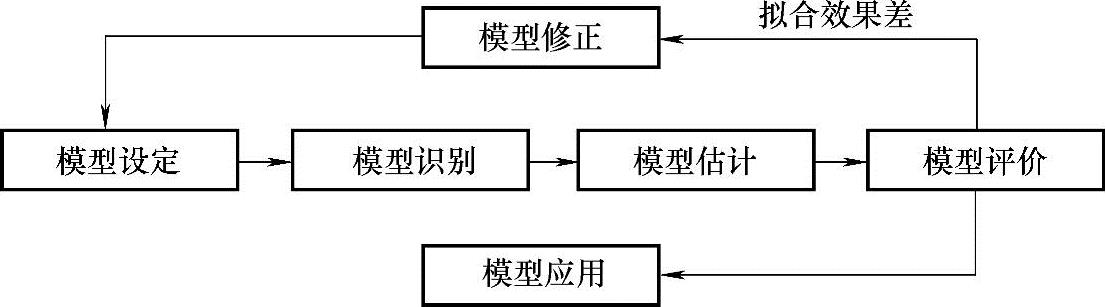
图4-2 结构方程模型运用（验证性因子分析）流程

第一步，模型设定。根据已有研究文献与相关理论构建一个初始模型，其中涉及潜变量与观测变量的关系以及各潜变量间的关系。如本书第3章所做的工作，初步提出了一个创新指标框架。

第二步，模型识别。很多时候，由于理论假设模型自身的设定就存在一些问题，模型难以得到理想的拟合参数和理想的关系，即模型不可识别。本章大量的工作就是对初始假设的指标结构进行模型拟合，在模型不可识别的情况下，对分指标结构进行调整。(www.daowen.com)

第三步，模型估计或模型拟合。在原模型的基础上，通过调整模型变量或变量关系，构建一个新的模型，并查看其模型拟合指数。通过对指标相关关系与指标结构的调整，使得拟合指数达到模型要求。

第四步，模型评价与修正。该过程既是上一轮拟合模型构建的结束，同时也是下一轮拟合模型的调整依据。

本书中，作者分别对三类项目的初始模型进行了多次调整，旨在得到理想的拟合指数与合理的指标关系。模型修正的方法可根据AMOS软件统计输出的改善模型拟合度进行检验。其中包括：拟合指数χ²、拟合优度指数（GFI）、Tucker-Lewis指数（TLI）、比较拟合指数（CFI）和估计误差均方根（RMSEA）等。通常情况下，检验一个模型是否合理需要参照这些拟合指数。其中的GFI、CFI的取值应落在0～1，其中如果大于0.85则认为该模型拟合较好。此外，RMSEA是结构方程模型中验证性因子分析最重要的参考指数，当RMSEA低于0.1时表示该模型拟合较好，而如果RMSEA低于0.05则表示拟合得非常好。