罗宾斯定理：一个图G有强连通定向，当且仅当G是连通的并且不含割边。

证明：充分条件。若图G有强连通定向，则G没有割边。

反证法：设图G有强连通定向且G有割边uv，若uv是图G的割边且定向为从v到u，则定向后的图D（G）中没有从u到v的有向迹；若定向为从u到v，则图D（G）中没有从v到u的有向迹，与D（G）是强连通相矛盾。

必要条件。若G不含割边，G一定存在一个定向，使定向后的图D（G）是强连通的。一个无向图可以看成一个有向图，只要用一对方向相反的边代替无向边即可。这样，首先将无向边看成是双向的。由于G连通，则这样定向的图是强连通的。对G的任一边uv，由于uv不是割边，则G中存在从v到u的迹不含边uv。将从v到u的迹看成有向的，并将边uv定向为从u到v的有向边。这样得到的图是强连通的。注意：这里没定向的边看成是双向的。同样地，在G中再取一条没有定向的边e，由于它不是割边，又边uv定向后的图仍是强连通的，于是图G-e中存在一条有向迹P连结e的端点u₁v₁，不妨设P是从u₁到v₁的有向迹，则将边e定向为从v₁到u₁，即边e成为定向后的有向边v₁u₁。这样定向了两条边的图仍然是强连通的，其中没有定向的边认为是双向的。重复前面的过程，则最终G的每条边会得到一个定向，使定向后的图D（G）是强连通的。

推论：一个图G有强连通定向，当且仅当G的任何一条边总是属于某一个圈。该推论与罗宾斯定理等价，互为充分必要条件。

证明：充分条件。若图G有强连通定向，则G的任何一条边总是属于某一个圈。

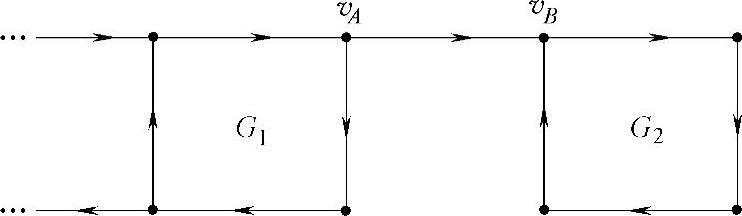
反证法：假设在强连通图G=（V，E）中，v_A∈V，v_B∈V，v_Av_B∈E，边v_Av_B不属于任何圈。对图G进行定向，若边v_Av_B为图G的有向边（即定向为v_A→v_B），则图G内所有能到达点v_A的点及其连通边形成一个强连通子图G₁，所有v_B能够到达的点及其连通边形成一个强连通子图G₂，如图3-1所示。显然，图G₂上的点不能到达图G₁，与图G内的点互相连通矛盾。

(www.daowen.com)

图3-1 主轨道网存在割边，不能强连通定向

若对图G进行定向后，边v_Bv_A为图G的有向边（即定向为v_B→v_A），可以类似方法证明。

必要条件。如果图G内任何一条边总是属于某一个圈，则该图不存在割边，由罗宾斯定理可证。

综上，图G有强连通定向，当且仅当G的任何一条边总是属于某一个圈。

图的定向定理：设G是强连通的混合图，对于图G的每条不是割边的边e，总可给边e一个定向使得到的混合图仍是强连通的。

证明：此定理的证明与罗宾斯定理的证明方法类似。