在应聘者招聘选拔的过程中，企业和应聘者之间的信息是相互不对称的。本文主要是站在企业招聘应聘者的角度来分析的。所以在企业和应聘者的博弈过程中，假设企业的信息是共同知识，也就是说，应聘者拥有企业的完全信息，但是企业不了解应聘者的具体信息。

1.企业招聘的博弈背景

对企业而言，它们希望找到那些高素质的应聘者，以使自身的利益最大化；对应聘者来说，他们总是希望得到更好的职位，获得更高的收入，而且往往不关心自己的素质如何，是不是能够胜任他们所应聘的职位。此外，还假定“所有参与人是理性人”是博弈参与人之间的公共知识，也就是说，企业家和应聘者相互之间都知道对方是理性人。

在应聘者招聘选拔的博弈中，有两个一般参与人，分别是应聘者和企业，用e和E表示。还有一个虚拟参与人“自然”，用N表示。根据能否胜任企业所提供的职位，把参与人应聘者分为两类：高素质者和低素质者。

假设在应聘者招聘选拔的博弈过程中，每个参与人只有两种行动可以选择。用AE={aE}={考核，不考核}表示企业的行动集，企业面对应聘者可以采取考核和不考核两种方式来决定是否录取应聘者；用Ae={ae}={应聘，不应聘}表示应聘者的行动集，应聘者面对企业发出的应聘信息，无论其素质是否满足岗位需求，他们都可以应聘，也可以不应聘。

用UE表示企业的得分，用Ue表示应聘者的得分，在应聘者招聘选拔博弈的过程中，各个参与人的得分如下：

（1）在应聘者高素质的情况下：

UE（考核，高素质应聘者）=C＜0；

UE（不考核，高素质应聘者）=0；

Ue（考核，高素质应聘者）=0；

Ue（不考核，高素质应聘者）=0。

（2）在应聘者低素质的情况下：

UE（不考核，低素质应聘者）=K＜0；

UE（考核，低素质应聘者）=B=C-K≥0；

Ue（考核，低素质应聘者）=0；

Ue（不考核，低素质应聘者）=M＞0。

在上述博弈支付中，假设C代表企业的考核成本。C＜0是因为对于高素质的应聘者来说，无论考核与否都不会给企业带来经营绩效方面的损失，但是在考核的情况下，企业会损失考核的成本，但是不能带来任何收益，即C＜0。

K代表低素质的应聘者应聘、企业不考核的情况下，所给企业带来的损失，即K＜0。

B分成两部分：B=C-K≥0。一般情况下，因招聘到低素质的应聘者所给企业带来的损失要大于企业的考核成本，那么B也就会在大多数情况下大于0。

M代表低素质的应聘者应聘、企业不考核的情况下，应聘者的收益。这时低素质的应聘者就会获得过高的工资，因此他的收益就为正值，即M＞0。

2.招聘的过程是一个不完全信息动态博弈

招聘的过程为：首先是应聘者素质的高低，高素质的应聘者可以完全胜任职位要求，而低素质的应聘者则不能胜任企业所提供的职位，如果让低素质的应聘者担任企业的一些岗位，会给企业带来一些损失；第二是应聘者选择是否向企业申请应聘；第三是企业决策是否招聘那些应聘的应聘者。由于低素质的应聘者可以通过隐瞒、欺骗等措施，以获得企业提供的职位，致使企业难以辨认这些应聘者的素质的高低。因此，企业在这个动态博弈中是具有不完全信息的。下图所示的博弈树就表示了这个不完全信息博弈，其中*P表示应聘者是高素质的概率（*P的具体数值可以根据行业经验、专业统计等方法获得）。

在图9-7中，初始点N表示应聘者在第一阶段被划分为高素质者和低素质者。应聘者当然很清楚自己的真实素质是高还是低，而企业不知道详细情况。在做出合理判断之前，不管应聘者是否把自己介绍为高素质者，企业首先要知道的是应聘者的素质概况，也就是说第一阶段应聘者素质的高低。用P(g)表示高素质者的概率，P(l)表示低素质者的概率，显然这两个概率只能根据经验或一般情况得出。其次，企业还应知道应聘者为高素质时把自己介绍为高素质者的概率和低素质时把自己介绍为高素质者的概率，分别表示为P(h|g)和P(h|l)。

根据贝叶斯法则有：

由P(l|h)=1-P(g|h)容易求出P(l|h)。

显然，高素质的应聘者肯定会把自己介绍为高素质者。无论企业考核与否，都不会给应聘者带来损失，因此高素质的应聘者把自己介绍为高素质者是理性策略，即P(h|g)=1；低素质者肯定也会把自己介绍为高素质者，若能得到自己想应聘的职位则有M＞0，若得不到自己想应聘的职位也不会有损失，所以理性选择也是把自己介绍为高素质者，即P(h|l)=1。

这时，企业的信息集包含两个决策结，表明企业在该阶段决策时不知道应聘者第一阶段的情况，也就是说，在应聘者第二阶段选择把自己介绍为高素质者的情况下，企业并不知道从决策树哪条路径过来的，因此无法针对两种不同的情况分别进行选择。企业虽然只有考核和不考核两种选择，但结果却有四种可能（如图9-7所示）。由此看来，企业要进行决策还需要进一步的信息或判断。

那么企业在自己的决策信息集，选择考核的期望收益为：

如果(C-B)×P*+B ＞0，即企业测评的期望得益为正值，则企业会选择考核；反之，如果(C-B)×P*+B ＜0，则企业会选择不考核。

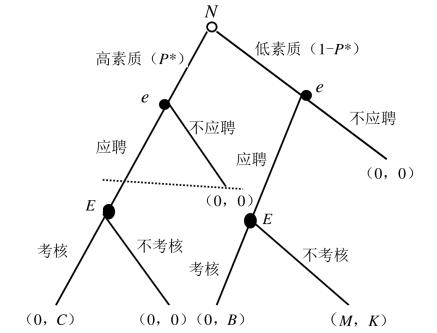
图9-7　企业招聘的动态博弈树

因为B=C-K，

所以(C-B)×P*+B ＞0可以转化为K×P*＞K-C ，(www.daowen.com)

由于K＜0，所以K×P*＞K-C 可以转化为P*＜，

即当P*＜时，企业应选择考核，以规避甄选错误人选的风险；

同理可得，当P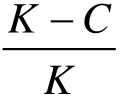*＞时，企业可以选择不考核。

容易验证，把自己介绍为高素质者（当P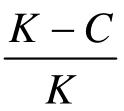*＜时考核）和把自己介绍为高素质者（当P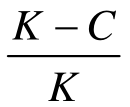*＞时不考核）均为精炼贝叶斯纳什均衡。也就是说，在不同的情况下，企业有条件地选择对应聘人是否考核。

3.结论

根据我们建立的模型，得出在企业招聘的不完全信息动态博弈的环节中，应聘者和企业选择策略：把自己介绍为高素质者（当P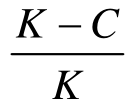*＜时考核）和把自己介绍为高素质者（当P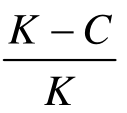*＞时不考核），为此博弈模型的精炼贝叶斯纳什均衡。

由此，我们可以得到启发：应聘者在应聘环节中，应尽量展示自己的优势以谋得岗位。而企业在招聘时应结合企业规模、招聘岗位重要程度、招聘成本等，并根据人力资源市场经验得出的所预计招聘人员在该专业从业人员中占据的比例等，选择符合企业经济效益最大化的方案，来确定是否进行考核以及考核的形式和规模等。

本章结束语

博弈论用来分析所观察到的决策主体相互影响时的现象，在给定的条件下寻求最优的解决办法。博弈可以划分为合作博弈和非合作博弈。博弈的要素包括参与人、行动、信息、策略、支付、结果和均衡。从参与人行动的先后顺序这个角度，博弈可以划分为静态博弈和动态博弈。从参与人对有关其他参与人（对手）的特征、策略集合及支付函数的知识这个角度，博弈可以划分为完全信息博弈和不完全信息博弈。

完全信息静态博弈条件是：每一个参与人对所有其他参与人（对手）的特征、策略空间及支付函数有准确的知识，而且博弈的参与人同时选择行动或虽非同时但后行动者并不知道前行动者采取了什么具体行动。策略式表述经常使用支付矩阵的形式来加以描述，适合于分析静态博弈。在每个参与人都有占优策略的情况下，占优策略均衡是一个非常合理的博弈结果；没有占优策略均衡时，有时可通过重复剔除严格劣策略找到重复剔除的占优均衡；纳什均衡是完全信息静态博弈解的一般概念，一个参与人的纳什均衡策略是面对其他参与人一个均衡策略时的最优选择。

完全信息动态博弈中，参与人的行动有先有后，后行动者自然会根据先行动者的选择进行策略的调整，先行动者也能理性地预期到这一点。扩展式表述经常使用博弈树的形式来加以描述，适合于分析动态博弈。子博弈精炼纳什均衡完善了纳什均衡的概念，将纳什均衡中包含的不合理策略剔除出去，要求参与者的决策在任何时点上都是最优的，是完全信息动态博弈的均衡解。子博弈是指从每一个行动选择开始至博弈结束这一阶段的行动过程。子博弈精炼纳什均衡可采用逆向归纳法求解。承诺行动可使不可置信威胁变得可置信，改变博弈的子博弈精炼纳什均衡。重复博弈使参与人可能会为长期利益暂时牺牲眼前利益从而选择不同的策略。

海萨尼转换是处理不完全信息博弈的标准方法。不完全信息静态博弈的结果是贝叶斯纳什均衡，贝叶斯纳什均衡是一种类型依赖型策略组合，给定自己的类型和其他参与人的类型的分布概率，这种策略组合使得每个参与人的期望效用达到了最大化。不完全信息动态博弈的结果是精炼贝叶斯纳什均衡，精炼贝叶斯纳什均衡的要点在于参与人要根据所观察到的其他参与人的行为来修正自己有关后者类型的判断，并由此选择自己的行动。判断的修正过程使用的是贝叶斯规则。

关键词：博弈论（game theory）纳什均衡（Nash equilibrium）子博弈精炼纳什均衡（subgame perfect Nash equilibrium）

复习思考题

1.给下列每一个博弈举出一个生活中的实例，并构建其矩阵式表述，进一步分析它的纳什均衡：智猪博弈；情侣博弈；斗鸡博弈；囚徒困境；零和博弈。

2.请准确地写出“纳什均衡”的定义，并举一个用矩阵图表示的实例，说明纳什均衡战略形成的条件。

3.纳什均衡与西方经济学中“一般均衡”有什么不同？

4.举例说明什么是共同知识。

5.寻找博弈均衡的方法你会哪几种？用你知道的方法举例予以解释。

6.用实例解释什么是博弈的期望收益。

7.单纯策略纳什均衡与混合策略纳什均衡有什么不同？

8.请举例解释混合策略，给出矩阵图，计算其混合策略纳什均衡。

9.举例说明什么是先动优势，什么是后动优势，并用博弈论的知识加以解释。

10.请分析海盗分赃问题。

11.指出重复博弈与序贯博弈的区别？

12.用囚徒困境博弈讨论有限次重复博弈问题和无限次重复博弈问题。用贴现值来寻求无限次重复博弈的纳什均衡。

【注释】

[1]支付矩阵一般只用于表示有两个参与人的有限博弈（finite game），因为当参与人多于两个时需要建立多个矩阵，这是很不方便的。有限博弈的条件：参与人是有限的；每个参与人的策略是有限的。

[2]这里的“严格”意味着式（9-7）中取“＞”，而不是“≥”。

[3]相应地，其余所有的策略，即≠被称为“劣策略”（dominated strategies）。

[4]当销售者是高价策略时，购买者的“高多低少”和“高多低多”策略都是多购，所以支付组合均为（4，1）；购买者的“高少低少”和“高少低多”策略都是少购，所以支付组合均为（2，7）。同样，可以找到销售者是低价策略时，两参与人的支付组合。

[5]比如说，最后决策结上的参与人的选择是在其他参与人都做出行动以后的，所以这个选择跟其他决策结处做出的选择无关；同样，倒数第二个决策结上的选择与倒数第三及以上的决策结处的选择无关„„

[6]减去企业的进入成本，合作时企业B的利润为40，不合作时企业B的利润为-10。

[7]这里的不完美信息，就是指其他参与人只知道某一参与人某些方面类型的概率分布，而不知道该参与人在这些方面的真实类型。