海萨尼转换使不完全信息博弈变得可以分析了。在此基础上，海萨尼提出了贝叶斯纳什均衡。贝叶斯纳什均衡是完全信息静态纳什均衡在不完全信息静态博弈上的扩展。

1.贝叶斯纳什均衡

贝叶斯纳什均衡可表述为：在不完全信息静态博弈中，参与人同时行动，没有机会观察到别人的选择。给定其他参与人的策略选择，每个参与人的最优策略依赖于自己的类型。由于每个参与人仅仅知道其他参与人有关类型的分布概率而不知道其真实类型，因而他不可能准确地知道其他参与人实际上会选择什么策略；但是，他能够正确地预测到其他参与人的选择如何依赖于各自的类型。因此，该参与人的决策目的就是在给定自己的类型和其他参与人的类型依从策略的情况下最大化自己的期望效用。也就是说，贝叶斯纳什均衡是一种类型依赖型策略组合，给定自己的类型和其他参与人的类型的分布概率，这种策略组合使得每个参与人的期望效用达到了最大化。

继续考虑市场进入的例子。企业B不知道企业A的真实类型，但假定它知道高成本的可能性为p，低成本的可能性为1-p。那么企业B选择进入时的期望利润为40×p +(-10)×(1-p)=50×p -10，而选择不进入时期望利润是0×p+0×(1-p)=0。通过简单计算得到：当p＞0.2时，企业B进入得到的期望利润大于不进入时的期望利润，从而进入才是最优的。假定p＞0.2，那么贝叶斯纳什均衡为：企业B选择进入，高成本企业A选择合作，低成本企业A选择不合作。(www.daowen.com)

2.贝叶斯纳什均衡的应用

贝叶斯纳什均衡的一个重要应用的领域是招标或拍卖方面。假设招标的办法是一级密封投标，让每个投标者将自己的标价写下装入信封，一同交给政府，信封打开后，政府选择标价最低者为中标者。这时，不同的投标者之间进行的就是一场博弈，假定每个投标者不知道其他投标者的真实生产成本而仅知其概率分布，那么，他在选择自己的报价时就会面临着一种考虑：报价越低，中标的可能性就越大；但另一方面，给定中标的情况，报价越低，利润越小。博弈分析证明，每个投标人的标价依赖于他的类型（这里为生产成本），但一般来说，贝叶斯均衡标价高于生产成本。二者之间的差异随投标人数的增加而减少。这就是说，让更多的企业参加投标，对政府是一件有利的事情。

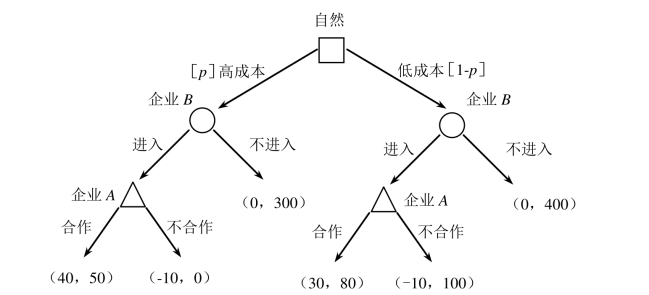
图9-6　海萨尼转换后的市场进入博弈