1934年，斯坦克尔伯格（Stackelberg）提出了描述寡头垄断市场的斯坦克尔伯格模型（Stackelberg model），这是一个完全信息动态博弈的例子。在这个模型中，有两个参与人：一个主导厂商A和一个追随厂商B；行动顺序是：主导厂商A首先确定产量QA，追随厂商B观察到厂商A的选择后再确定自己的产量QB。各厂商的行动空间都是自己的产量，支付为各自的利润函数。下面是这一模型的动态博弈描述，并用逆向归纳法予以求解。

用QA、QB分别表示厂商A和厂商B的产量；CA（QA ）和CB（QB ）表示两者的成本函数；P=P（QA+QB ）表示需求函数的逆函数，其中P是价格。厂商A和厂商B的利润函数分别为：

按照逆向归纳求解的方法，首先来计算厂商B对厂商A可能的选择所作出的反应，即求厂商B的反应函数。厂商B达到支付（即利润）最大时，有：

由此得到厂商B对厂商A的反应函数：

将式（9-16）代入到厂商A的利润函数中：

为了求解厂商A利润最大化的产量，对式（9-17）求一阶导数：

可得到厂商A的均衡产量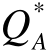。将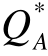代入厂商B对厂商A的反应函数，即式（9-16）中，可得到厂商B的均衡产量?。最终得到两厂商的子博弈精炼纳什均衡Q*=（）。

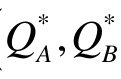如果需求函数的逆函数为P=T-（QA+QB ），其中，T为一常数，两寡头的产量QA与QB之和为市场总产量。假定两厂商的单位成本不变等于c，计算可知两寡头厂商各自的产量为QA=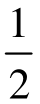·（T-c ），QB=·（T-c）。也就是说，此时，子博弈精炼纳什均衡的策略组合是

这就是斯坦克尔伯格模型的逆向归纳求解的结果。把这一结果与古诺模型比较，可以看出，在古诺模型中，每个厂商的产量为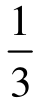·（T-c），总产量为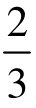·（T-c）；而斯坦克尔伯格模型的总产量为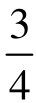·（T-c）。因为两个模型的市场需求曲线都一样，所以斯坦克尔伯格模型中的价格要低一些。另外，在斯坦克尔伯格模型中，先行动的厂商A实际上也可以选择古诺产量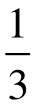·（T-c），这时厂商B对此的反应是也将选择古诺产量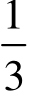·（T-c）。厂商A本来可以选择古诺产量而选择了斯坦克尔伯格产量，这说明厂商A借助先行的机会，获得了更多的利润，这就是所谓的“先行者优势”。这是因为，厂商A一旦将产品生产出来就无法改变，从而使厂商B不得不认为这个威胁是可置信的。

案例9.4 强盗分赃

假设5个强盗抢到100枚金币然后分赃。制定了如下的分赃规则：首先由第1个人提出方案，全体表决。超过绝对半数同意才实施该方案，否则提案者将被丢进海里。然后第2个人继续提案，直到剩下最后一个人。问题是：第1个人可以获得多少金币？他应该如何提案？

这是一个完全信息动态博弈。在博弈的视角里，参与博弈的这5个强盗（按照提案顺序依次给他们命名为甲、乙、丙、丁、戊）都是完全理性的经济人，追求自身的最大得分，本案例中的最大得分则指：在不被丢进海里的前提下，获得最多数量的金币。在规则中可以看出，提案是否被采纳还要取决于后续提案者的投票，然而我们发现按顺序找出提案策略显然太繁琐，那么不妨采取逆向归纳法找到最优策略。(www.daowen.com)

1.“戊”一人独得

假设前面4人都因得不到超过绝对半数的同意票，而都被扔到海里时，那么现在轮到第5个强盗戊提案时，他将独吞所有金币。因此得分情况可以表示如下：

2.“丁”提案通过

由上述情况倒推第4个强盗丁的行为，丁如果想要自己的提案通过，这时还剩2人，需要获得2票同意，他只能选择将全部金币都给戊才能通过。此时得分情况可以表示如下：

3.“丙”提案通过

当丙进行提案时，还剩下3人，丙需要获得2票同意，才能使提案通过。这意味着丙只需争取到丁、戊当中的一票即可。在上一情况中戊已经拿到了全部金币，无法超越，争取这一票显然没有意义；而只要增加丁一点点金币，他将同意丙的提案，剩下的金币将属于丙所有。此时得分情况可以表示如下：

4.和上面的推论道理一样，我们可以得到当“乙”提案通过时的情形

5.最后，我们得到“甲”提案通过时的最佳分配方案

我们发现结论是第一个人最多可以获得97枚金币，他的提案为：依次分给大家97、0、1、0、2枚金币。这个结果多少有些出乎意料，但是又包含了深刻的博弈哲理。

资料来源：吴玮.数学爱好者.2006年，第2期