如果采用参与者同时行动的静态博弈分析方法分析动态博弈，得到的纳什均衡中就会存在不合理的均衡策略。泽尔腾通过对动态博弈的分析完善了纳什均衡的概念，定义了“子博弈精炼纳什均衡”。这一概念的意义就是将纳什均衡中包含的不合理策略剔除出去，要求参与者的决策在任何时点上都是最优的。

1.纳什均衡与不可置信威胁

仍以市场销售的博弈为例。为了构造这个动态博弈的策略式表述，先来分析销售者和购买者的策略空间。销售者是先行动的，有两种策略：高价和低价。购买者是后行动的，根据销售者的行动，就有四种策略：高价时多购，低价时少购；高价时多购，低价时多购；高价时少购，低价时少购；高价时少购，低价时多购。将这四种策略分别简记为：高多低少；高多低多；高少低少；高少低多。市场销售博弈的支付矩阵见表9-13所示^[4]。

表9-13　市场销售博弈的策略式表述

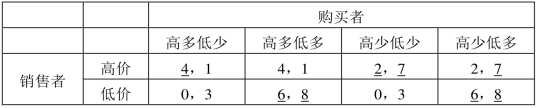
纳什均衡的概念适用于所有的博弈，而不仅仅是参与人同时行动的静态博弈。但博弈分析的目的是预测参与人的行为，纳什均衡给出的策略可能并不是一个非常合理的结果。表9-13对市场销售的博弈分析使用的是静态分析方法，得到三个纳什均衡：（高价，高少低少）；（低价，高多低多）；（低价，高少低多）。但究竟哪一个均衡实际上会发生，静态分析难以确定。更严重的是，在纳什均衡中，参与人在选择自己的策略时，把其他参与人的策略当作是给定的，同时也不考虑自己的选择如何影响对手。所以说，纳什均衡允许了“不可置信威胁（incredible threats）”的存在。不可置信威胁是指，对于先行动的参与人来说，后行动的参与人的选择空间依赖于先行动者的选择，在先行动者已做出行动选择的前提下，有一些对先行动者不利的策略将不会被后行动者选择，即这些策略是不可置信的。

例如，对于策略组合（高价，高少低少）来说，意味着不管销售者采取高价策略还是低价策略，购买者将始终会少购，在这个策略威胁下，消费者就不会采取低价策略，否则会得到的支付为0。销售者并不会相信这个威胁。在销售者真的选择低价时，如果购买者是理性的就会选择多购：少购得到的支付是3，多购却是8。可见，纳什均衡（高价，高少低少）就是不可置信的。

2.子博弈的概念

为了给出子博弈精炼纳什均衡的概念，需要先定义“子博弈”的概念。子博弈（subgame）是指从每一个行动选择（即一个决策结）开始至博弈结束这一阶段的行动过程，是原博弈的一部分。市场销售博弈的博弈树如图9-3的Ⅰ图所示；决策点x和它的后续点构成一个子博弈，如图9-3的Ⅱ图所示；决策点y和它的后续点也构成一个子博弈，如图9-3的Ⅲ图所示。另外，原博弈自身也是自己的一个子博弈。这样，市场销售博弈共有三个子博弈。

3.子博弈精炼纳什均衡

泽尔腾定义的子博弈精炼纳什均衡是纳什均衡的一个重要改进，分开了动态博弈中的“合理的纳什均衡”和“不合理的纳什均衡”。正如纳什均衡是完全信息静态博弈解的一般概念一样，子博弈精炼纳什均衡是完全信息动态博弈解的一般概念。子博弈精炼纳什均衡定义如下：一个扩展式表述的策略组合s*=(，如果是其原博弈的纳什均衡，又给出其每一个子博弈上的纳什均衡，那么它就是一个子博弈精炼纳什均衡。

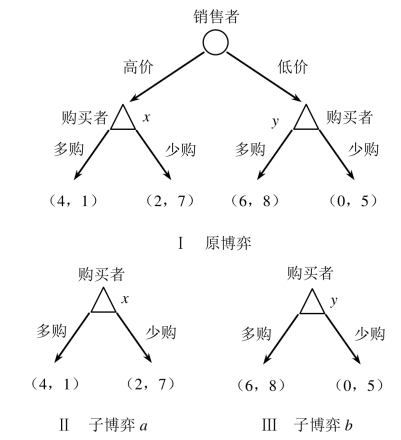
图9-3　市场销售博弈的博弈树(www.daowen.com)

仍以市场销售博弈为例分析子博弈精炼纳什均衡的概念。除了原博弈外，其他两个子博弈只有购买者一人做出决策。通过前面的分析已经知道，该博弈共有三个纳什均衡：（高价，高少低少）、（低价，高多低多）和（低价，高少低多）。在子博弈a中，购买者的最优选择“少购”，在子博弈b中，购买者的最优选择“多购”。纳什均衡（高价，高少低少）中购买者的均衡战略“高少低少”，给出了子博弈a上的纳什均衡（少购），却没有给出子博弈b上的纳什均衡，所以，（高价，高少低少）不是子博弈精炼纳什均衡。纳什均衡（低价，高多低多）中购买者的均衡战略“高多低多”，给出子博弈b上的纳什均衡（多购），却没有给出子博弈a上的纳什均衡，所以，（低价，高多低多）也不是子博弈精炼纳什均衡。而对于纳什均衡（低价，高少低多）中购买者的均衡战略“高少低多”来说，既给出子博弈a上的纳什均衡，也给出了子博弈b上的纳什均衡（即高价时将少购，低价时将多购），所以，（低价，高少低多）才是子博弈精炼纳什均衡。于是，销售者采取低价策略、购买者多购即是最终的结果。

子博弈精炼纳什均衡剔除了不可置信的纳什均衡，在每一个子博弈上都能给出纳什均衡，所以参与者的决策在任何时点上都是最优的，它就是完全信息动态博弈的均衡解。

4.逆向归纳法求解子博弈精炼纳什均衡

如果没有任何两个参与人同时行动，逆向归纳法可以比较方便地求解子博弈精炼纳什均衡。找到博弈最后的决策结，在每一个决策结上，参与人都有一个（也可能是多个，这时可任选一个，因为这与此前行动的参与人的选择无关^[5]）最优选择，从该决策结开始的子博弈的纳什均衡。然后回溯到倒数第二个决策结，找出该决策结上的参与人的最优选择。这个最优选择与上一步找出的最后决策结的最优选择一起构成了从倒数第二个决策结开始的子博弈的纳什均衡。如此向上回溯，直到第一个决策结，这时得到的纳什均衡对应着每一个子博弈的纳什均衡，所以就是这个博弈的子博弈精炼纳什均衡。

用逆向归纳法求解市场销售博弈中的子博弈精炼纳什均衡如下。最后的两个决策结上，购买者选择的策略是“高少低多”，即销售者高价时购买者少购，销售者低价时购买者多购。如图9-4的Ⅰ图所示，图中的虚线表示两个子博弈上的纳什均衡的策略。继续向上找到第一个决策结，因为购买者预测到会按照“高少低多”的策略行动，会选择“低价”策略。所以用逆向归纳法得到的子博弈精炼纳什均衡是（低价，高少低多），如图9-4的Ⅱ图所示。

图9-4　逆向归纳法求解子博弈精炼纳什均衡

5.承诺与子博弈精炼纳什均衡

有些纳什均衡之所以不是子博弈精炼纳什均衡，是因为包含了不可置信威胁。但是，如果参与人能在博弈之前做出“承诺行动”，使不可置信威胁变得可置信，博弈的子博弈精炼纳什均衡就会相应改变。承诺行动（commitment）是指当事人在不施行这种不可置信的威胁时，就会付出更大的代价。尽管这一代价不一定发生，但承诺行动会给当事人带来很大的好处，因为它可以改变均衡结果。

假设企业A是市场上某产品的唯一供给者，垄断利润为300，但面临企业B可能进入的竞争威胁，企业的进入成本为10。企业A有两种可选策略：合作和不合作。合作意味着维持高价，寡头利润共为100（各得50）；不合作表现为采用降低价格使利润为0^[6]。这个市场进入博弈的博弈树如图9-5所示。

在上面的例子中，子博弈精炼纳什均衡的策略组合是（进入，合作），即企业B进入、企业A合作。但是，如果企业A通过某种承诺行动使自己的“不合作”威胁变得可置信，企业B就不敢进入了。比如，企业A与第三者打赌，如果企业B进入后他选择了合作，他就付给第三者100单位。此时，不合作就变成可置信威胁。因为如果企业B进入后，企业A合作带来50单位利润扣除100单位利润的赌注，将得到-50单位净利润，而不合作所得0利润，所以不合作比合作更有利。有了这个赌注，企业B就不敢贸然进入了，在位者实际上无需支付赌注便可得到300单位的垄断利润。一般来说，承诺行动的成本越高，威胁的可置信度就越高。

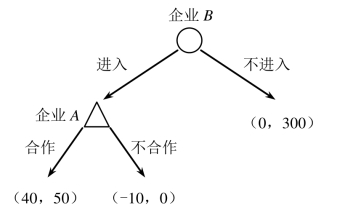
图9-5　市场进入博弈的博弈树