如果重复剔除劣策略后剩下的策略组合是唯一存在的，那么该博弈是重复剔除占优可解的（dominance solvable），否则该博弈不是重复剔除占优可解的。但对于相当多的博弈，是无法使用重复剔除劣策略的方法找到均衡解的，求解这些博弈就需要新的方法。

1.纳什均衡的定义

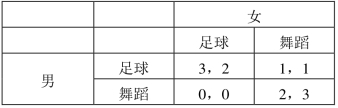
首先我们来看一个经典的博弈——情侣博弈，也叫作性别之战（battle of the sexes）。一男一女谈恋爱，周末安排业余活动，要么看足球比赛，要么看舞蹈演出。男士爱好足球，女士更喜欢舞蹈，但他们宁愿在一起而不愿分开。支付矩阵见表9-9所示。在这个博弈中有两个均衡策略：（足球，足球）和（舞蹈，舞蹈）。就是说，一方选择了看足球，另一方也会去看足球；同样，一方选择了看舞蹈，另一方也会去看舞蹈。究竟哪一种均衡会发生就不得而知了，但这两个策略组合都是纳什均衡。

表9-9　性别之战

下面我们给出纳什均衡的正式定义：考虑n个参与人的策略式表述博弈G={s1,...,sn ;u1,...,un}，如果对于每一个参与者i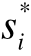，是给定其他参与人选择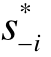=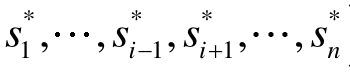（的情况下第i个参与人的最优策略，即：

那么，策略组合s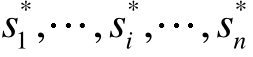*=（是一个纳什均衡。

也就是说，一个参与人的纳什均衡策略是面对其他参与人一个均衡策略时的最优选择。为了理解纳什均衡的含义，设想n个参与人在博弈之前协商达成一个协议，规定每一个参与人选择一个特定的策略。令B代表这个协议，其中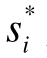是协议规定的第i个参与人的策略。显然，只有当遵守协议带来的效用大于不遵守协议时的效用时，一个人才会遵守这个协议。如果没有任何参与人有积极性不遵守这个协议，那么这个协议是可以自动实施的，这个协议就构成一个纳什均衡；否则，它就不是一个纳什均衡。也可以这么说，如果预测s'=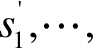（是博弈的一个结果但这个结果不是一个纳什均衡，那么至少存在某些参与人有积极性偏离这个结果。

运用上述定义来检查一个特定的策略组合是否是一个纳什均衡。在囚徒困境中，（坦白，坦白）是一个纳什均衡，而（抵赖，抵赖）不是一个纳什均衡，因为给定同伙选择抵赖，自己选择抵赖时得到-1，选择坦白时得到0，因而抵赖不是自己的最优策略；同样，（坦白，抵赖）和（抵赖，坦白）也不是纳什均衡。在性别之战中，（足球，足球）是一个纳什均衡，因为一旦形成这个策略组合的结果，任何一方的偏离都会造成自己支付的减少，例如，女的此时去看舞蹈将把自己的支付从2降到1；同样，（舞蹈，舞蹈）也是一个纳什均衡，其他策略组合都不是纳什均衡。

案例9.3 古诺模型与纳什均衡

古诺模型是早期的寡头垄断模型。它是法国经济学家古诺于1838年提出的。古诺模型通常被作为博弈分析的出发点。古诺模型是一个只有两个寡头厂商的简单模型，该模型也被称为“双头模型”。

古诺模型分析的是两个出售矿泉水的生产成本为零的寡头垄断厂商的情况。古诺模型的假定是：市场上有A、B两个厂商生产和销售相同的产品，它们的生产成本相同；它们共同面临的市场的需求曲线是线性的，A、B两个厂商都准确地了解市场的需求曲线；A、B两个厂商都是在已知对方产量的情况下，各自确定能够给自己带来最大利润的产量，即每一个厂商都是消极地以自己的产量去适应对方已确定的产量。

古诺模型中，寡头做出生产决策时的关键在于如何决定自己的最优产量，来实现利润最大化。现在，博弈参与人即是两个寡头厂商，分别是厂商A和厂商B；每个厂商的策略是选择产量；支付是利润，它是两个厂商产量的函数。可见，这就是一个完全信息静态博弈，其均衡实际上是一个纳什均衡。

用QA、QB分别表示厂商A和厂商B的产量；CA（QA ）和CB（QB ）表示两者的成本函数；P=P（QA+QB ）表示反需求函数，其中P是价格。厂商A和厂商B的利润函数分别为：

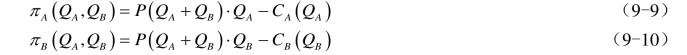
纳什均衡意味着每个厂商在对方选择的产量策略下自身达到支付（即利润）最大。为了求得厂商利润最大化时的产量，对每个厂商的利润函数求一阶偏导数并令其等于零：

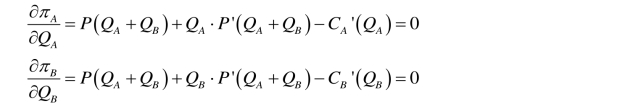
上述两个一阶条件分别隐含定义了两个厂商产量之间的反应函数，整理可得：

反应函数意味着每个厂商的最优策略（产量）是另一个厂商的策略（产量）的函数，两个反应函数的交叉点（即两个方程的解）就是纳什均衡Q*=（）。

资料来源：刘骏民.微观经济学.科学出版社，2007年

2.求解纳什均衡的一个简单方法

当参与人的策略空间很大时，要按上述方法检查每一个策略组合是不是纳什均衡是一件很费时的繁琐工作。在两人优先策略博弈中，解纳什均衡的一个简单方法如下。首先考虑A的策略，对于每一个B的给定的策略，找出A的最优策略，在其对应的支付下画一横线，再用类似的方法找出B的最优策略。在完成这个过程后，如果某个支付组合的两个数字下都有线，这个支付组合所对应的策略组合就是一个纳什均衡。

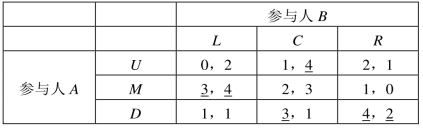
表9-10给出了一个例子。对应B的三个不同策略L、C、R，A的最优策略分别是M、D、D；对应A的三个不同策略U、M、D，B的最优策略分别是C、L、R，因此，（M，L）和（D，R）两种策略组合都是纳什均衡。

表9-10　寻求纳什均衡

通过对纳什均衡与占优策略均衡以及重复剔除的占优均衡的分析，可知它们之间的关系如下：每一个占优策略均衡、重复剔除的占优均衡一定是纳什均衡，但并非每一个纳什均衡都是占优策略均衡或重复剔除的占优均衡。这是因为，一个参与人的占优策略是对于所有其他参与人的任何策略组合的最优选择，自然也一定是对于所有其他参与人的某个特定策略的最优选择；而一个参与人的纳什均衡策略只要求是对于其他参与人均衡策略（这是一个或几个特定策略）的最优选择。所以说，占优策略均衡和重复剔除的占优均衡是特殊的纳什均衡，它们所要求的条件比纳什均衡的条件要严格。例如，在囚徒困境的博弈中，（坦白，坦白）是一个占优策略均衡、重复剔除的占优均衡，也是一个纳什均衡；在智猪博弈中，（按，等待）是一个重复剔除的占优均衡，也是一个纳什均衡；在表9-10的博弈中，（M，L）和（D，R）是一个纳什均衡，但不是一个重复剔除的占优均衡（无法通过重复剔除劣策略的办法找到均衡解），更不是占优策略均衡。

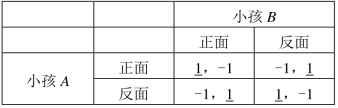
当然，并不是所有的完全信息静态博弈都存在这种形式的纳什均衡。例如，在掷币游戏中，每个参与人的支付直接用其赢得或输掉的硬币数量来表示：赢得一枚硬币的支付为1，输掉一枚硬币的支付为-1。掷币游戏的支付矩阵见表9-11所示。经过分析，任何一个支付组合的数字下面都不会同时有线，因为这种零和博弈的任何一方都不会选择失败，所以单纯形式的纳什均衡并不存在，我们需要寻找其他形式的纳什均衡。

表9-11　掷币游戏(www.daowen.com)

3.混合策略纳什均衡

博弈双方按照一定的概率随机选择策略，即在博弈中，博弈方的决策内容不是确定性的某一个策略，而是在一些策略中随机选择的概率分布，这样的决策我们称为“混合策略”。

在博弈G={s1,...,sn ;u1,...,un}中，博弈参与人i的策略空间为si=｛si1,„,sik｝，则博弈方i以概率分布pi=（pi1,„,pik）随机在其k个可选策略中选择的“策略”，称为一个“混合策略”，其中0≤pij≤1对j=1,„,k都成立，且pi1+„+pik=1。

相对于这种以一定概率分布在一些策略中随机选择的混合策略，确定性的具体的策略我们称为“单纯策略”，而我们原来意义上的纳什均衡，即任何博弈方都不愿单独改变策略的单纯策略组成的策略组合现在可称为“单纯策略纳什均衡”。当然，单纯策略也可以看作混合策略的特例。混合策略可以看作单纯策略的扩展。

引进了混合策略的概念以后，我们可将纳什均衡的概念扩大到包括混合策略的情况。对各博弈方的一个策略组合，不管它是单纯策略组成的还是混合策略组成的，只要满足各博弈方都不会想要单独偏离它，我们就称之为一个纳什均衡。如果确实是一个严格意义上的混合策略组合构成的纳什均衡，就称为“混合策略纳什均衡”。

比如硬币博弈中，博弈双方都以（1/2，1/2）的概率分布随机选择正面和反面的混合策略组合，就是一个混合策略纳什均衡。其期望得益：

显然，这是个零和博弈。

下面，我们以社会福利博弈为例说明如何求解混合策略纳什均衡。如表9-12所示，博弈参与人是政府和流浪汉，政府的策略空间是{救济，不救济}，流浪汉的策略空间是{找工作，游荡}，政府希望流浪汉能够积极找工作，但是这个博弈不存在单纯策略纳什均衡。下面寻找混合策略纳什均衡。

表9-12　社会福利博弈支付矩阵

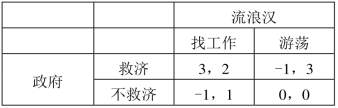
假定政府的混合策略为σG=(θ,1-θ)（即政府以θ的概率选救济，1-θ的概率选不救济），流浪汉的混合策略为σL=(γ,1γ-)（即流浪汉以γ的概率选找工作，以1-γ的概率选游荡）。则政府的效用函数为：

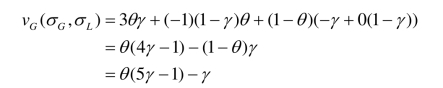
求其微分可得到政府最优化的一阶条件：

因此，在混合策略均衡，流浪汉以0.2的概率选择寻找工作，以0.8的概率选择游荡。

问题是，解政府的最优化问题得到的却是流浪汉的混合策略。对此可作如下解释：首先假定最优混合策略是存在的。给定流浪汉选择混合策略（γ,1-γ），政府选单纯策略救济（即θ =1）的期望效用为：

选择单纯策略不救济（即θ = 0）的期望效用为：

如果一个混合策略是政府的最优选择，则一定意味着政府在救济与不救济之间是无差异的，即：

上式意味着γ=0.2。即若γ＜0.2政府将选择不救济；如果γ≥0.2，政府将选择救济；只有当γ*=0.2时，政府才会选择混合策略或任何单纯策略。

要找出政府的均衡混合策略，需考虑流浪汉的最优化问题。流浪汉的效用函数为：

最优化一阶条件为：

该结论可解释为：若θ < 0.5，流浪汉的最优选择是找工作；若θ > 0.5，其最优选择是游荡；只有当θ = 0.5时，他才选择混合策略或任何单纯策略。

纳什均衡要求每个参与人的混合策略是给定对方的混合策略下的最优选择。故θ*=0.5，r*=0.2是唯一的混合策略纳什均衡。即在均衡时，政府以0.5的概率选救济，0.5的概率选不救济；流浪汉以0.2的概率选找工作，以0.8的概率选游荡。

假定政府认为流浪汉找工作的概率严格小于0.2，则政府的唯一最优选择是单纯策略不救济；但若政府以1的概率选不救济，流浪汉的最优选择是找工作，这又将导致政府选择救济，流浪汉则选游荡„„。因此，r < 0.2不构成纳什均衡。类似地，假定政府认为流浪汉找工作的概率严格大于0.2，则政府的唯一最优选择是单纯策略救济；但若政府以1的概率选救济，流浪汉的最优选择是游荡。因此，r > 0.2不构成纳什均衡。容易验证，θ < 0.5和θ > 0.5也都不构成纳什均衡。