在每个参与人都有占优策略的情况下，占优策略均衡是一个非常合理的预测，但在绝大多数博弈中，占优策略均衡是不存在的。尽管如此，在有些博弈中，仍可以应用占优策略的逻辑找出均衡。

我们来考虑一下“智猪博弈（boxed pigs game）”例子。猪圈里围着两头猪，一头大猪，一头小猪。猪圈的一头有一个猪槽，另一头安装了一个按钮，控制着猪食的供应。按下一按钮会有8个单位的猪食进槽，但按下按钮的猪需要付出2个单位的成本。若大猪先到，大猪吃到7个单位，小猪只能吃1个单位；若同时到，大猪吃5个单位，小猪吃3个单位；若小猪先到，大猪和小猪各吃4个单位。表9-8的Ⅰ表列出对应不同策略组合的支付水平，如第一格表示两头猪同时按下按钮，就会同时走到猪食槽，大猪吃5个单位，小猪吃3个，扣除2个单位的成本，支付水平分别为3和1。其他情形可以类推。

表9-8　智猪博弈与重复剔除的占优均衡(www.daowen.com)

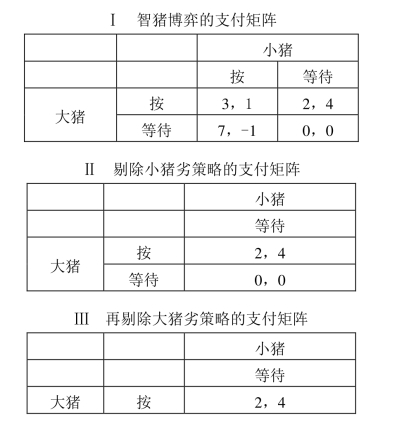
显然，这个博弈没有占优策略均衡，因为尽管“等待”是小猪的占优策略，但大猪没有占优策略。大猪的最优策略依赖于小猪的策略。如果小猪选择“等待”，大猪的最优策略是“按”；如果小猪选择“按”，大猪的最优策略是“等待”。显然，这个博弈没有占优策略均衡。但这个博弈可以通过“重复剔除严格劣策略（iterated elimination of strictly dominated strategies）”找到均衡，即首先找到参与人的劣策略，把这个劣策略除去，重新构造一个不包含这个劣策略的新的博弈；然后再剔除新博弈中的劣策略，直至找到唯一的策略组合。这种博弈的均衡解，称为“重复剔除的占优均衡（iterated dominance equilibrium）”。通过分析可以看出，无论大猪如何选择，“等待”都是小猪的最优策略，所以应首先剔除掉小猪的劣策略“按”，见表9-8的Ⅱ表所示。在剔除掉这个策略后的新的博弈中，小猪只有一个策略“等待”，大猪仍有两个策略，但此时，“等待”已成为大猪的劣策略，剔除这个策略，剩下的唯一策略组合是（按，等待），支付组合为（2，4），见表9-8的Ⅲ表所示。

“智猪博弈”告诉我们，谁先去按下按钮，就会造福全体，但多劳却并不一定多得。比如，在某个行业，不仅存在一些小企业，还有一些其他生产能力和销售能力更强的大公司。那么，小企业完全没有必要自己去研发新产品或者投入大量广告做产品宣传，只要采用跟随战略即可，等待市场上占主导地位的大公司开拓本行业的主导品牌和最新产品的市场需求，而将自己的品牌定位在较低价格上，以享受主导品牌的强大广告所带来的市场机会。