1.占优策略

由于每个参与人的效用（支付）是博弈中所有参与人的策略组合的函数，因此一般来说，某个参与人的最优策略选择会依赖于其他参与人的策略选择。但在一些特殊的博弈中，一个参与人的最优策略可能并不依赖于其他参与人的策略选择，就是说，不论其他参与人选择什么策略，此人的最优策略是唯一的，这样的最优策略被称为占优策略（dominant strategy）。

案例9.2 制药公司的销售大战

斯特恩巴赫是费城的一个家庭保健医生，她很奇怪为什么辉瑞公司（Pfizer）的五位不同推销员重复上门到她的诊所推销同样的止痛药——Betra及Celebrex。她在贮藏室里的一个像冰箱大的柜子里已装满了Bextra和Celebrex，她说：“众多的推销员重复同样的产品，没有任何新意，实在是离奇。”

长达十年的招聘狂潮使制药业的推销员人数增加到90000人，为原来人数的三倍。制药业人士笃信：只要推销员向医生推销一种药越频繁，医生越有可能多开此药。据统计，2003年制药业在推销员工上花费为120多亿美元，在药物广告上花费为27.6亿美元。根据联邦政府的报告，美国国内在处方药上的支出激增14%，达到1610亿美元。

尽管如此，没有任何一家制药商愿意第一个单方面裁军。葛兰素史克公司（GlaxoSmithKline）的推销员队伍是如此壮大：它只需要七天就可以联系到美国80%以上的医生。“这有必要吗？”葛兰素史克的CEO加涅尔说：“应该说是没有必要，但是如果我的竞争对手能而我做不到，我们就处于劣势。这的确是以最坏可能的方式进行的军备竞赛。”

“拥有众多的推销员不是竞争优势的源泉”，默克公司的主席和CEO吉尔马丁补充说。他说制药商通过发现新药来获得优势。然而，默克公司2001年起在美国已增加了1500名推销员，使得总数达到约7000人。

既然谁都知道拥有众多的推销员并不是竞争优势的源泉，那为什么各家制药公司的推销员仍然在不断膨胀呢？

资料来源：周林.商业战略决策：博弈论的应用

在上述销售大战的博弈中，我们可以看到，每一家制药商在广告开支方面都有两种策略选择：节约或扩张。显然，不管其他竞争对手选择什么策略，每一家制药商的最优策略都是“扩张”，就像加涅尔所说的，“如果我的竞争对手能而我做不到，我们就处于劣势”。

2.占优策略均衡

下面具体说明博弈中占优策略均衡的概念。为了把一个特定的参与人与其他参与人区别开来，用s-i表示由除i之外的所有参与人的策略组成的向量：

如果对于所有的s-i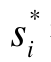，都是第i个参与人的严格最优选择^[2]，即：

(www.daowen.com)

那么，就被称为第i个参与人的（严格）占优策略（dominant strategy）^[3]。进而，所有参与人占有策略的组合策略s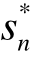*=(,...,,)称为占优策略均衡（dominant-strategy equilibrium）。

囚徒困境（prisoner’s dilemma）讲的是两个嫌疑犯作案后被警察抓住，分别被关在不同的屋子里审讯。警察告诉他们：如果两人都坦白，各判刑8年；如果两个都抵赖，各判3年（或许因证据不足）；如果其中一人坦白另一人抵赖，坦白的释放，不坦白的判刑10年（这有点“坦白从宽，抗拒从严”的味道）。表9-5给出了囚徒困境模型的表述。这里，每个囚徒都有两种选择：坦白或抵赖。表中每一格的两个数字代表对应两个囚徒选择组合下各自的刑期，其中第一个数字是囚徒A的刑期，第二个数字为囚徒B的刑期。

表9-5　囚徒困境

在这个博弈中，每个囚徒都有两种可选择的策略：坦白或抵赖。显然，不论另一囚徒选择什么策略，每个囚徒的最优策略是“坦白”。比如说，如果B选择坦白，A选择坦白时支付为-8，选择抵赖时的支付为-10，因而坦白比抵赖好；如果B选择抵赖，A坦白时的支付为0，抵赖时的支付为-3，因而坦白还是比抵赖好。就是说，“坦白”是囚徒A的占优策略。同样，“坦白”也是B的占优策略。那么这样一来，（坦白，坦白）就构成一个占优策略均衡。

囚徒困境反映了一个深刻的问题，即个人理性与团体理性的冲突。如果每个人都选择抵赖，各判刑1年，显然比都判刑8年好。但这个帕累托改进做不到，因为它不满足个人理性要求，（抵赖，抵赖）不是一个均衡。换个角度看，即使两个囚徒在作案之前建立一个攻守同盟（都不坦白），这个攻守同盟也没有用，因为没有人有积极性遵守协定。这就是合作博弈与非合作博弈的区别。

事实上，在一个博弈里，如果所有参与人都有占优策略存在，那么，占优策略均衡是可以预测到的唯一的均衡。应该指出的是，占优策略均衡只要求每个参与人是理性的，而不要求每个参与人知道其他参与人是理性的。这是因为，不论其他参与人是否是理性的，占优策略总是一个理性参与人的最优选择。但是，占优策略均衡的存在前提是要求所有参与人都有占优策略存在，否则就不可解。

3.博弈的规则与均衡

下面我们再来看一个自由贸易中关税政策的博弈案例。

博弈的参与人是两个国家A、B，两个国家在贸易政策方面分别可以选择征收关税和自由贸易两种策略。如果A、B两国都向对方征收关税，则两国分别获得1单位的收益；如果A国向B国征收关税，B国对A国实行自由贸易，则A国获得5单位的收益，B国损失1单位的收益；反之亦然；如果A、B两国都选择自由贸易政策，则两国分别获得3单位的收益。如表9-6所示。

表9-6　关税政策博弈的支付矩阵

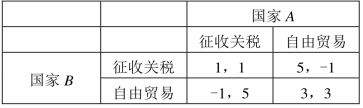
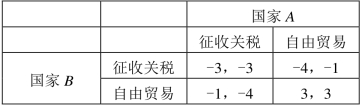
这个博弈的占优策略均衡是（征收关税，征收关税），从结果来看也是一种囚徒困境。因为双方征收关税的结果显然不如双方自由贸易。如何解决这个问题呢？这就需要从博弈规则入手。假设现在有一个第三方组织比如WTO，博弈双方都加入了WTO，那么现在WTO的规则之一就是鼓励成员国减免关税，最终实现自由贸易，否则会受到严厉的惩罚。在有惩罚机制的新规则之下，我们再来求解下面的新关税政策博弈就会发现，现在的占优策略均衡已经变成了（自由贸易，自由贸易），见表9-7。这一结果说明了博弈的规则对于均衡的影响是很重要的。

表9-7　新关税政策博弈的支付矩阵