下面我们分别从总收益与总成本和边际收益与边际成本的角度来分析追求利润最大化的厂商将如何确定其实际的产量水平，以此确定利润最大化的条件。

1.利润最大化的数学推导

利润等于总收益减总成本，即：

利润最大化就是总收益超出总成本的差距最大。由于收益与成本都是产量的函数，所以利润也是产量的函数。厂商要实现利润最大化，就是要确定一个适当的产量，使总收益超出总成本最大。这就转化为求π的极大值问题。当总收益函数和总成本函数都是连续可导时，π取极大值时的条件是：

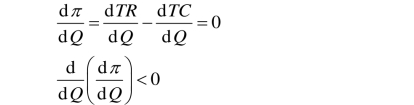
因为：

即得到利润最大化的必要条件：

也就是说，厂商达到利润最大化时，必然处于边际收益等于边际成本的产量点。再考虑条件此时，在边际收益等于边际成本的产量点达到利润最大化；小于这个产量时，边际收益大于边际成本，即增加一单位产量带来的收益仍将大于所付出的成本，故厂商仍会增加产量；大于这个产量时，边际收益小于边际成本，即增加一单位产量带来的收益将会小于所付出的成本，故厂商就会减少产量。

案例6.7 经理的一些成本考虑(www.daowen.com)

对边际收益等于边际成本这一规则的运用，取决于经理对边际成本的估算能力。为获得有用的成本估算，经理应在心里牢记以下三条指导原则：

第一，可能的话，平均可变成本不应用来替代边际成本。边际成本和平均成本接近固定时，它们之间几乎没有差别。但当边际成本和平均成本都迅速增加时，要决定生产多少数量，用平均可变成本则会产生误导。举例来说，假设一个公司有以下成本资料：

当前产量：每天100单位，其中25单位属加班生产

材料成本：每天500美元

人工成本：每天2000美元（正常时间），加班1000美元（加班时间）

平均可变成本容易计算——劳动成本加材料成本（3500美元）除以每天100单位，为35美元/单位。但恰当的成本是边际成本，它可计算如下：不管生产多少产量，每单位材料成本固定不变，所以边际成本为500美元/100＝5美元/单位。因为劳动的边际成本仅涉及加班劳动，这100个单位中的25个单位是在加班时间内生产的，所以这样可得到劳动的边际成本。加班时间里每单位产量的平均报酬为1000美元/25＝40美元/单位，这是对劳动的边际成本的一个很好的估算。因而，每多生产一单位产量的边际成本为45美元（材料边际成本加劳动边际成本），这比35美元的平均可变成本要大。如果依赖平均可变成本进行决算，那他将生产过多的产量。

第二，厂商的会计分类账（accounting ledger）的单独科目可能有两个组成部分，但只有其中一个部分涉及边际成本。例如，假设经理想削减生产，他减少一些雇员的工作时间，并裁减其他雇员。但被裁减的雇员工资可能无法准确衡量此时生产的边际成本，因为工会经常要求企业支付被裁减员工的部分工资。在这种情况下，因增加产量而增加边际成本将不同于产量下降相同数量时所节约的边际成本，后者等于节省的劳动成本减去所需支付给裁减员工的工资之差额。

第三，决定机会成本时应包括所有的机会成本。假定一家百货商店想出售儿童家具，经理决定利用商店三楼本来摆放电器的一部分空间现在来摆放家具，而不是建一个新的销售点。这部分空间的边际成本就是假如商店继续销售电器而赚得的利润除以家具的销量，这样测算出来的机会成本可能要比商店实际为这部分建筑所支付的成本大得多。

这三条准则可以帮助经理人员正确地衡量边际成本。如果做不到这一点，将会导致产量过高或过低，并因此减少利润。

摘自blog.sina.com.cn

2.利润最大化的图形表示

显然，图6-12中的产量点Q0可使厂商获得最大化利润。在该产量点，总成本曲线切线的斜率等于总收益曲线切线的斜率，即MR=MC。且有在边际收益曲线与边际成本曲线交点的左边，边际收益大于边际成本，厂商会扩大产量直至边际收益等于边际成本；在边际收益曲线与边际成本曲线交点的右边，边际收益小于边际成本，厂商会降低产量直至边际收益等于边际成本。