导致规模报酬发生变动的原因比较复杂的，我们分别对规模报酬递增和规模报酬递减的原因进行归纳分析。

1.规模报酬递增的原因

发生规模报酬递增的因素主要有如下几个：

一是几何关系作用。一个100×100米的厂房，其使用面积为10000平方米，需要的围墙为400米；而一个100×200英尺的厂房，其使用面积比前一个大一倍，但所需建立的围墙只有600米，或者说，比前一个只需增加50%的材料。又如，管道的直径增大两倍，其流量的增加会大于两倍；载重汽车装载能力的增加也大于其自身重量的增加。

二是专业分工与协作程度的提高。较大的生产规模可以使工人提高专业化和分工的程度，并能够使用更加专门的特殊的机器和工具从事某些特殊的工作，这可以大大提高劳动生产率。

三是某些技术和投入的不可分性。有些技术和投入，如电子计算机、自动化装配线、平炉等，只能在经营规模或产量足够大时才有可能使用。所以，一个较大的工厂可能比规模相同的两个小工厂更有效率，因为它可以利用小工厂不能利用的某些技术和投入。

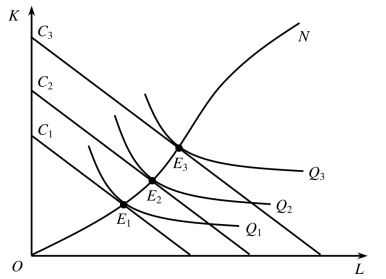
图5-14　扩展线的推导

四是概率因素。规模报酬递增，也可能产生于概率方面的原因。例如，由于较大数量的顾客的总体行为更趋向于稳定，所以，厂商不必按照与规模扩大的同一比例增加其存货。

2.规模报酬递减的原因

上述导致规模报酬递增的因素，其作用最终会受到限制。当生产规模达到一定点后，进一步扩大规模，其报酬或者说收益会发生递减的变化。即使是几何关系，其作用也是有限的，如随着建筑物变得越来越大，屋顶和墙壁的建造可能不得不采用更结实的材料；当管道和盒子变得更大时，也必须用更厚更坚固的材料来制造；载重汽车越重，越可能需要一种特制的底盘。

进一步说，当生产规模扩大到一定点后，协调和控制大规模经营的困难会增加，随着管理层次的增加，信息在从工人到最高管理层以及相反的传递过程中会损失或失真，通信联系的渠道会变得更加复杂和更难于把握，决策的制定需要更多的时间和补充，这类问题在所有大型组织中都会发生。这表明管理和协调大厂商的困难可能是造成规模报酬递减的一个源泉。

本章结束语

生产是指把投入变为产出的行为。企业就是指实现投入变为产出的行为者。企业主要有三种组织形式：个人企业、合伙制企业和公司制企业。在分析企业行为时，微观经济学假定企业是以利润最大化为目标。

生产函数是指每个时期内所使用的各种生产要素的数量与该时期内所能生产的某种商品的最大量之间的关系。假设投入的生产要素只有劳动和资本两种，生产函数写为：Q=f(L,K)。生产一定量某种产品所要求投入的各种生产要素之间的配合比例被称为技术系数。生产有短期和长期之分，以能否变动所有投入要素为划分依据。

假定可变投入只有劳动，资本为不变投入，短期生产函数写为：Q=f(L,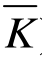。总产量是指从一定量该种生产要素中所获得的产量的总和；平均产量是指平均每个单位生产要素所生产的产量，等于劳动生产的产量除以该要素的投入量；每增加一单位劳动所引起的总产量变动，被称为边际产量。边际生产力递减规律是指在其他生产要素的投入量保持不变的情况下，如果连续追加相同数量的某种生产要素，其产量的增量在达到某一点后将会下降。劳动的边际产量低于平均产量，但边际产量仍为正的生产阶段是可变要素生产的合理阶段。

长期内劳动和资本均为可变要素，生产函数为：Q=f(L,K)。厂商生产某一数量的产品时，两种生产要素可以相互替代。等产量曲线是指在生产技术不变时，能够生产同一产量的两种生产要素的各种有效组合的轨迹。在等产量曲线图中，从坐标原点出发的射线表示的是具有相同比例的所有劳动和资本的组合，射线的斜率就等于劳动与资本的这一不变比例。边际技术替代率是指在技术水平不变的条件下，维持相同的产量水平，每增加一单位的某种生产要素所能替代的另一种生产要素的数量之比。边际技术替代率可以表示为两种生产要素的边际产量之比。

等成本线是指在既定的成本和生产要素价格条件下生产者可以购买到的两种生产要素的各种不同数量组合的轨迹。假定厂商投入的成本和产品价格不变，利润最大化就可以看作是产量最大化或可看作是成本的最小化。此时，厂商最佳投入组合，即生产者均衡点可以表述为两种生产要素的边际产量之比等于其价格之比。

扩展线是生产技术不变的条件下厂商在长期内扩大生产规模所采用的最佳投入组合点的轨迹，是一条特殊的等斜线。规模报酬也称规模收益，指的是由规模变动所引起的产量的变动，可分为规模报酬递增、规模报酬递减和规模报酬不变三种情况。发生规模报酬递增的因素主要是几何关系作用、专业分工与协作程度的提高、某些技术和投入的不可分性以及概率因素等；规模报酬递增的因素的作用最终会受到限制，当生产规模达到一定点后，进一步扩大规模，其报酬或者说收益会发生递减的变化。

关键词：生产函数（production function）等产量曲线（isoquant curve）等成本线（isocost curve）边际技术替代率（marginal rate of technical substitution）规模报酬（returns to scale）

复习思考题(www.daowen.com)

1.某企业在短期生产中的生产函数为Q=-L3+24L2+240L，计算企业在下列情况下的L的取值范围。①在第Ⅰ阶段；②在第Ⅱ阶段；③在第Ⅲ阶段。

2.如果某企业仅生产一种产品，并且唯一可变要素是劳动，没有固定成本。其短期生产函数为Q=-0.1L3+3L2+8L，其中，Q是每月的产量，单位为吨；L是雇佣工人数，试问：

（1）欲使劳动的平均产量达到最大，该企业需要雇佣多少工人？

（2）要使劳动的边际产量达到最大，其应该雇佣多少工人？

（3）在其平均可变成本最小时，生产多少产量（Q）？

3.已知某企业的生产函数为Q=5L+12K－2L2－K2，其中，PL=3，PK=6，总成本TC=160，试求该企业的最优要素组合。

4.已知生产函数为Q=KL－0.5L2－0.32K2，Q表示产量，K表示资本，L表示劳动。令上式的K=10。

（1）写出劳动的平均产量（APL）函数和边际产量（MPL）函数。

（2）分别计算当总产量、平均产量和边际产量达到极大值时厂商雇佣的劳动。

（3）证明当APL达到极大时，APL=MPL=2。

5.边际产量曲线、总产量曲线和平均产量曲线之间存在怎样的关系？

6.等产量曲线有哪些特征？这些特征的经济含义是什么？

7.简述规模报酬变动规律及其成因。

8.请比较说明消费者行为理论与生产者行为理论。

9.某企业主管想增加聘用一单位工人来生产一批产品，那么他应该更多考虑的是劳动的平均产量还是劳动的边际产量？为什么？

10.如果甲、乙两个地区生产同样的产品——布料，甲生产1平方米所需要的工人是5人，而乙只需要2人即可。试问：我们能否判定乙的生产效率要比甲的生产效率高？为什么？

11.规模报酬的递增、不变和递减这三种情况与一种要素可变的报酬递增、不变和递减的三种情况的区别何在？

12.用图形说明总产量、平均产量与边际产量的变动关系。

【注释】

[1]也就是说，当平均产量最大时，边际产量与平均产量相等。这表明了一个简单的数学理论：如果总量的增量（即边际量）大于平均量，平均量将增加；如果总量的增量小于平均量，平均量将减少。