假定厂商投入的成本和产品价格不变，利润最大化就可以看作是产量最大化或可看作是成本的最小化。这样，厂商选择最佳投入组合原则就可以设定为成本既定条件下的产量最大化或产量既定条件下的成本最小化。

1.成本既定条件下的产量最大

如图5-12所示，有一条等成本线C和三条等产量曲线Q0，Q1，Q2。等成本线C与其中一条等产量曲线Q1相切于E点，该点就是生产者的均衡点。

为什么E点是均衡点呢？对于产量水平高于Q1的等产量曲线来说，如等产量曲线Q2，与等成本线C既无交点也无切点，这表明在既定成本条件下无法实现等产量曲线Q2，与等成本线C既无交点也无切点，这表明在既定成本条件下无法实现等产量曲线Q2所代表的产量；对于产量水平低于Q1的等产量曲线来说，如等产量曲线Q0，虽然与等成本线C相交于A点和B点，但此时厂商在不增加成本的情况下，沿着既定的等成本线C由A点向E点或由B点向E点移动来改变投入要素的数量组合，就可以增加产量。所以，在投入成本既定的条件下，厂商的产量最大点，或者说，生产者的均衡点，就是厂商既定的等成本线与其相切的那条等产量曲线的切点。

2.产量既定条件下的成本最小

如图5-13所示，有三条等成本线C0、C1、C2和一条等产量曲线Q，其中C0＜C1＜C2。等产量曲线Q与其中一条等成本线C1相切于E点，该点就是生产者的均衡点。

这是因为，等成本线C0虽然表示的成本较低，但它与既定的等产量曲线Q既无交点也无切点，也就无法实现等产量曲线Q代表的产量；等成本线C2虽然与既定的等产量曲线Q相交于A点和B点，但它表示的成本过高，沿着等产量曲线Q由A点向E点或由B点向E点移动，都可以获得相同的产量而成本下降。所以，在产量既定的条件下，厂商的成本最小点，或者说，生产者的均衡点，就是厂商既定的等产量曲线与其相切的那条等成本线的切点。

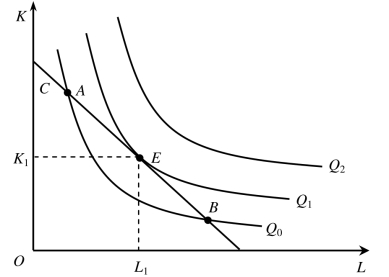
图5-12　成本既定条件下的产量最大化

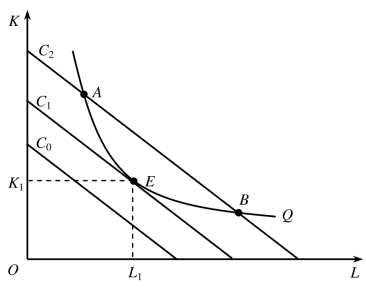
图5-13　产量既定条件下的成本最小化

案例5.5 引进自动分拣机是好事还是坏事(www.daowen.com)

近年来我国邮政行业实行信件分拣自动化，引进自动分拣机代替工人分拣信件，也就是多用资本而少用劳动。假设某邮局引进一台自动分拣机，只需一人管理，每日可以处理10万封信件。如果用人工分拣，处理10万封信件需要50个工人。在这两种情况下都实现了技术效率。但是否实现了经济效率还涉及价格。处理10万封信件，无论用什么方法，收益是相同的，但成本如何则取决于机器与人工的价格。假设一台分拣机为400万元，使用寿命10年，每年折旧为40万元，再假设利率为每年10% ，每年利息为40万元，再加上分拣机每年维修费与人工费用5万元，这样使用分拣机的成本为85万元。假设每个工人工资1.4万元，50个工人共70万元，使用人工分拣成本为70万元。在这种情况下，使用自动分拣机实现了技术效率，但没有实现经济效率；而使用人工分拣既实现了技术效率，又实现了经济效率。

从上面的例子中可以看出，在实现了技术效率时，是否实现了经济效率就取决于生产要素的价格。如果仅仅从企业利润最大化的角度看，可以只考虑技术效率和经济效率。这两种效率的同时实现也就是实现了资源配置效率。当然，如果从社会角度看问题，使用哪种方法还要考虑每种方法对技术进步或就业等问题的影响。

摘自www.lntvu.com

3.最优投入组合的条件分析

从上面的分析中可见，成本既定条件下的产量最大化或是产量既定条件下的成本最小化，两者都是厂商必须在等产量曲线与等成本线相切的切点进行生产。在等成本线与等产量曲线相切的切点，两种生产要素的投入组合调整到了最优状态，也就是达到了生产者均衡状态。在均衡点上，等产量曲线的斜率等于等成本线的斜率，即：

式（5-17）表示：当两种生产要素的边际技术替代率与其价格之比相等时，达到了最优投入组合。反过来说，当两者不相等时，就不可能达到最优投入组合。

因为边际技术替代率可以表示为两种生产要素的边际产量之比，故式（5-18）可写为：

从而有：

上式表明厂商最佳投入组合（生产成本的最小化或既定成本产出的最大化），也可以表述为：两种生产要素的边际产量之比等于其价格之比，或者说，最后一单位支出成本无论用来买哪一种生产要素所获得的边际产量都相等。